
Electric field screening
Encyclopedia
Screening is the damping of electric field
s caused by the presence of mobile charge
carriers. It is an important part of the behavior of charge-carrying fluid
s, such as ionized gases (classical plasmas) and conduction electron
s in semiconductor
s and metal
s.
In a fluid composed of electrically charged constituent particles, each pair of particles interact through the Coulomb force
,
 .
.
This interaction complicates the theoretical treatment of the fluid. For example, a naive quantum mechanical calculation of the ground-state energy density yields infinity, which is unreasonable. The difficulty lies in the fact that even though the Coulomb force diminishes with distance as 1/r², the average number of particles at each distance r is proportional to r², assuming the fluid is fairly isotropic
. As a result, a charge fluctuation at any one point has non-negligible effects at large distances.
In reality, these long-range effects are suppressed by the flow of the fluid particles in response to electric fields. This flow reduces the effective interaction between particles to a short-range "screened" Coulomb interaction.
For example, consider a fluid composed of electrons. Each electron possesses an electric field which repels other electrons. As a result, it is surrounded by a region in which the density of electrons is lower than usual. This region can be treated as a positively-charged "screening hole". Viewed from a large distance, this screening hole has the effect of an overlaid positive charge which cancels the electric field produced by the electron. Only at short distances, inside the hole region, can the electron's field be detected.
and Hückel (1923), dealt with a stationary point charge embedded in a fluid. This is known as electrostatic screening.
Consider a fluid of electrons in a background of heavy, positively-charged ions. For simplicity, we ignore the motion and spatial distribution of the ions, approximating them as a uniform background charge. This is permissible since the electrons are lighter and more mobile than the ions, provided we consider distances much larger than the ionic separation. In condensed matter physics
, this model is referred to as jellium
.
Let ρ denote the number density
of electrons, and φ the electric potential
. At first, the electrons are evenly distributed so that there is zero net charge at every point. Therefore, φ is initially a constant as well.
We now introduce a fixed point charge Q at the origin. The associated charge density
is Qδ(r), where δ(r) is the Dirac delta function
. After the system has returned to equilibrium, let the change in the electron density and electric potential be Δρ(r) and Δφ(r) respectively. The charge density and electric potential are related by the first of Maxwell's equations
, which gives
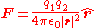 .
.
To proceed, we must find a second independent equation relating Δρ and Δφ. We consider two possible approximations, under which the two quantities are proportional: the Debye-Hückel approximation, valid at high temperatures, and the Fermi-Thomas approximation, valid at low temperatures.
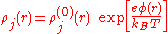
where kB is Boltzmann's constant. Perturbing in φ and expanding the exponential to first order, we obtain
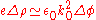
where

The associated length λD ≡ 1/k0 is called the Debye length
. The Debye length is the fundamental length scale of a classical plasma.
and at low temperatures. (The former condition corresponds, in a real experiment, to keeping the fluid in electrical contact at a fixed potential difference with ground
.) The chemical potential μ is, by definition, the energy of adding an extra electron to the fluid. This energy may be decomposed into a kinetic energy T and the potential energy -eφ. Since the chemical potential is kept constant,
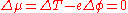 .
.
If the temperature is extremely low, the behavior of the electrons comes close to the quantum mechanical
model of a free electron gas. We thus approximate T by the kinetic energy of an additional electron in the free electron gas, which is simply the Fermi energy
EF. The Fermi energy is related to the density of electrons (including spin degeneracy) by
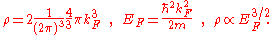
Perturbing to first order, we find that
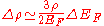 .
.
Inserting this into the above equation for Δμ yields
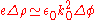
where
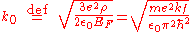
is called the Fermi-Thomas screening wave vector.
This follows from a previous result for the free electron gas, which is a model of non-interacting electrons, whereas the fluid which we are studying contains a Coulomb interaction. Therefore, the Fermi-Thomas approximation is only valid when the electron density is high, so that the particle interactions are relatively weak.

which is known as the screened Poisson equation
. The solution is

which is called a screened Coulomb potential. It is a Coulomb potential multiplied by an exponential damping term, with the strength of the damping factor given by the magnitude of k0, the Debye or Fermi-Thomas wave vector. Note that this potential has the same form as the Yukawa potential. This screening yields a dielectric function .
.
to respond at wave-vectors shorter than the Fermi wave-vector. This is related to the Gibbs phenomenon
, where fourier series for functions that vary rapidly in space are not good approximations unless a very large number of terms in the series are retained. In physics this is known as Friedel oscillations, and applies both to surface and bulk screening. In each case the net electric field does not fall off exponentially in space, but rather as an inverse power law multiplied by an oscillatory term. The area of many-body physics devotes considerable effort to quantum-mechanical screening, which is very relevant to condensed matter physics.
Electric field
In physics, an electric field surrounds electrically charged particles and time-varying magnetic fields. The electric field depicts the force exerted on other electrically charged objects by the electrically charged particle the field is surrounding...
s caused by the presence of mobile charge
Electric charge
Electric charge is a physical property of matter that causes it to experience a force when near other electrically charged matter. Electric charge comes in two types, called positive and negative. Two positively charged substances, or objects, experience a mutual repulsive force, as do two...
carriers. It is an important part of the behavior of charge-carrying fluid
Fluid
In physics, a fluid is a substance that continually deforms under an applied shear stress. Fluids are a subset of the phases of matter and include liquids, gases, plasmas and, to some extent, plastic solids....
s, such as ionized gases (classical plasmas) and conduction electron
Electron
The electron is a subatomic particle with a negative elementary electric charge. It has no known components or substructure; in other words, it is generally thought to be an elementary particle. An electron has a mass that is approximately 1/1836 that of the proton...
s in semiconductor
Semiconductor
A semiconductor is a material with electrical conductivity due to electron flow intermediate in magnitude between that of a conductor and an insulator. This means a conductivity roughly in the range of 103 to 10−8 siemens per centimeter...
s and metal
Metal
A metal , is an element, compound, or alloy that is a good conductor of both electricity and heat. Metals are usually malleable and shiny, that is they reflect most of incident light...
s.
In a fluid composed of electrically charged constituent particles, each pair of particles interact through the Coulomb force
Coulomb's law
Coulomb's law or Coulomb's inverse-square law, is a law of physics describing the electrostatic interaction between electrically charged particles. It was first published in 1785 by French physicist Charles Augustin de Coulomb and was essential to the development of the theory of electromagnetism...
,
 .
.This interaction complicates the theoretical treatment of the fluid. For example, a naive quantum mechanical calculation of the ground-state energy density yields infinity, which is unreasonable. The difficulty lies in the fact that even though the Coulomb force diminishes with distance as 1/r², the average number of particles at each distance r is proportional to r², assuming the fluid is fairly isotropic
Isotropy
Isotropy is uniformity in all orientations; it is derived from the Greek iso and tropos . Precise definitions depend on the subject area. Exceptions, or inequalities, are frequently indicated by the prefix an, hence anisotropy. Anisotropy is also used to describe situations where properties vary...
. As a result, a charge fluctuation at any one point has non-negligible effects at large distances.
In reality, these long-range effects are suppressed by the flow of the fluid particles in response to electric fields. This flow reduces the effective interaction between particles to a short-range "screened" Coulomb interaction.
For example, consider a fluid composed of electrons. Each electron possesses an electric field which repels other electrons. As a result, it is surrounded by a region in which the density of electrons is lower than usual. This region can be treated as a positively-charged "screening hole". Viewed from a large distance, this screening hole has the effect of an overlaid positive charge which cancels the electric field produced by the electron. Only at short distances, inside the hole region, can the electron's field be detected.
Electrostatic screening
The first theoretical treatment of screening, due to DebyePeter Debye
Peter Joseph William Debye FRS was a Dutch physicist and physical chemist, and Nobel laureate in Chemistry.-Early life:...
and Hückel (1923), dealt with a stationary point charge embedded in a fluid. This is known as electrostatic screening.
Consider a fluid of electrons in a background of heavy, positively-charged ions. For simplicity, we ignore the motion and spatial distribution of the ions, approximating them as a uniform background charge. This is permissible since the electrons are lighter and more mobile than the ions, provided we consider distances much larger than the ionic separation. In condensed matter physics
Condensed matter physics
Condensed matter physics deals with the physical properties of condensed phases of matter. These properties appear when a number of atoms at the supramolecular and macromolecular scale interact strongly and adhere to each other or are otherwise highly concentrated in a system. The most familiar...
, this model is referred to as jellium
Jellium
Jellium, also known as the uniform electron gas or homogeneous electron gas , is a quantum mechanical model of interacting electrons in a solid where the positive charges are assumed to be uniformly distributed in space whence the electron densityis a uniform quantity as well in space...
.
Let ρ denote the number density
Number density
In physics, astronomy, and chemistry, number density is an intensive quantity used to describe the degree of concentration of countable objects in the three-dimensional physical space...
of electrons, and φ the electric potential
Electric potential
In classical electromagnetism, the electric potential at a point within a defined space is equal to the electric potential energy at that location divided by the charge there...
. At first, the electrons are evenly distributed so that there is zero net charge at every point. Therefore, φ is initially a constant as well.
We now introduce a fixed point charge Q at the origin. The associated charge density
Charge density
The linear, surface, or volume charge density is the amount of electric charge in a line, surface, or volume, respectively. It is measured in coulombs per meter , square meter , or cubic meter , respectively, and represented by the lowercase Greek letter Rho . Since there are positive as well as...
is Qδ(r), where δ(r) is the Dirac delta function
Dirac delta function
The Dirac delta function, or δ function, is a generalized function depending on a real parameter such that it is zero for all values of the parameter except when the parameter is zero, and its integral over the parameter from −∞ to ∞ is equal to one. It was introduced by theoretical...
. After the system has returned to equilibrium, let the change in the electron density and electric potential be Δρ(r) and Δφ(r) respectively. The charge density and electric potential are related by the first of Maxwell's equations
Maxwell's equations
Maxwell's equations are a set of partial differential equations that, together with the Lorentz force law, form the foundation of classical electrodynamics, classical optics, and electric circuits. These fields in turn underlie modern electrical and communications technologies.Maxwell's equations...
, which gives
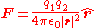 .
.To proceed, we must find a second independent equation relating Δρ and Δφ. We consider two possible approximations, under which the two quantities are proportional: the Debye-Hückel approximation, valid at high temperatures, and the Fermi-Thomas approximation, valid at low temperatures.
Debye-Hückel approximation
In the Debye-Hückel approximation, we maintain the system in thermodynamic equilibrium, at a temperature T high enough that the fluid particles obey Maxwell-Boltzmann statistics. At each point in space, the density of electrons with energy j has the form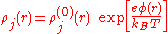
where kB is Boltzmann's constant. Perturbing in φ and expanding the exponential to first order, we obtain
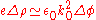
where

The associated length λD ≡ 1/k0 is called the Debye length
Debye length
In plasma physics, the Debye length , named after the Dutch physicist and physical chemist Peter Debye, is the scale over which mobile charge carriers screen out electric fields in plasmas and other conductors. In other words, the Debye length is the distance over which significant charge...
. The Debye length is the fundamental length scale of a classical plasma.
Fermi-Thomas approximation
In the Fermi-Thomas approximation, we maintain the system at a constant chemical potentialChemical potential
Chemical potential, symbolized by μ, is a measure first described by the American engineer, chemist and mathematical physicist Josiah Willard Gibbs. It is the potential that a substance has to produce in order to alter a system...
and at low temperatures. (The former condition corresponds, in a real experiment, to keeping the fluid in electrical contact at a fixed potential difference with ground
Ground (electricity)
In electrical engineering, ground or earth may be the reference point in an electrical circuit from which other voltages are measured, or a common return path for electric current, or a direct physical connection to the Earth....
.) The chemical potential μ is, by definition, the energy of adding an extra electron to the fluid. This energy may be decomposed into a kinetic energy T and the potential energy -eφ. Since the chemical potential is kept constant,
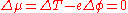 .
.If the temperature is extremely low, the behavior of the electrons comes close to the quantum mechanical
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
model of a free electron gas. We thus approximate T by the kinetic energy of an additional electron in the free electron gas, which is simply the Fermi energy
Fermi energy
The Fermi energy is a concept in quantum mechanics usually referring to the energy of the highest occupied quantum state in a system of fermions at absolute zero temperature....
EF. The Fermi energy is related to the density of electrons (including spin degeneracy) by
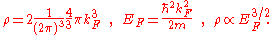
Perturbing to first order, we find that
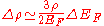 .
.Inserting this into the above equation for Δμ yields
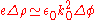
where
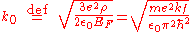
is called the Fermi-Thomas screening wave vector.
This follows from a previous result for the free electron gas, which is a model of non-interacting electrons, whereas the fluid which we are studying contains a Coulomb interaction. Therefore, the Fermi-Thomas approximation is only valid when the electron density is high, so that the particle interactions are relatively weak.
Screened Coulomb interactions
Our results from the Debye-Hückel or Fermi-Thomas approximation may now be inserted into the first Maxwell equation. The result is
which is known as the screened Poisson equation
Screened Poisson equation
In Physics, the screened Poisson equation is the following partial differential equation:\left[ \Delta - \lambda^2 \right] u = - f...
. The solution is

which is called a screened Coulomb potential. It is a Coulomb potential multiplied by an exponential damping term, with the strength of the damping factor given by the magnitude of k0, the Debye or Fermi-Thomas wave vector. Note that this potential has the same form as the Yukawa potential. This screening yields a dielectric function
 .
.Quantum-mechanical screening
In real metals, electrical screening is more complex than described above in the Fermi-Thomas theory. This is because Fermi-Thomas theory assumes that the mobile charges (electrons) can respond at any wave-vector. However, it is not energetically possible for an electron within or on a Fermi surfaceFermi surface
In condensed matter physics, the Fermi surface is an abstract boundary useful for predicting the thermal, electrical, magnetic, and optical properties of metals, semimetals, and doped semiconductors. The shape of the Fermi surface is derived from the periodicity and symmetry of the crystalline...
to respond at wave-vectors shorter than the Fermi wave-vector. This is related to the Gibbs phenomenon
Gibbs phenomenon
In mathematics, the Gibbs phenomenon, named after the American physicist J. Willard Gibbs, is the peculiar manner in which the Fourier series of a piecewise continuously differentiable periodic function behaves at a jump discontinuity: the nth partial sum of the Fourier series has large...
, where fourier series for functions that vary rapidly in space are not good approximations unless a very large number of terms in the series are retained. In physics this is known as Friedel oscillations, and applies both to surface and bulk screening. In each case the net electric field does not fall off exponentially in space, but rather as an inverse power law multiplied by an oscillatory term. The area of many-body physics devotes considerable effort to quantum-mechanical screening, which is very relevant to condensed matter physics.

