
Duhamel's principle
Encyclopedia
In mathematics
, and more specifically in partial differential equations, Duhamel's principle is a general method for obtaining solutions to inhomogeneous
linear evolution equations like the heat equation
, wave equation
, and vibrating plate
equation. It is named for Jean-Marie Duhamel
who first applied the principle to the inhomogeneous heat equation that models, for instance, the distribution of heat in a thin plate heated from beneath. For linear evolution equations without spatial dependency, such as a harmonic oscillator
, Duhamel's principle reduces to the method of variation of parameters technique for solving linear inhomogeneous ordinary differential equations.
The philosophy underlying Duhamel's principle is that it is possible to go from solutions of the Cauchy problem
(or initial value problem) to solutions of the inhomogeneous problem. Consider, for instance, the example of the heat equation modeling the distribution of heat energy u in Rn. The initial value problem is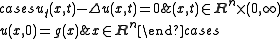
where g is the initial heat distribution. By contrast, the inhomogeneous problem for the heat equation is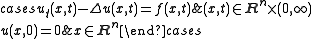
corresponds to adding an external heat energy ƒ(x,t)dt at each point. Intuitively, one can think of the inhomogeneous problem as set of homogeneous problems each starting afresh at a different time slice t = t0. By linearity, one can add up (integrate) the resulting solutions through time t0 and obtain the solution for the inhomogeneous problem. This is the essence of Duhamel's principle.

with spatial domain D in Rn, of the form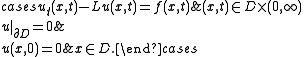
where L is a linear differential operator that involves no time derivatives.
Duhamel's principle is, formally, that the solution to this problem is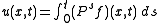
where Psƒ is the solution of the problem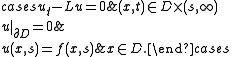
Duhamel's principle also holds for linear systems (with vector-valued functions u), and this in turn furnishes a generalization to higher t derivatives, such as those appearing in the wave equation (see below). Validity of the principle depends on being able to solve the homogeneous problem in an appropriate function space and that the solution should exhibit reasonable dependence on parameters so that the integral is well-defined. Precise analytic conditions on u and f depend on the particular application.
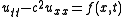
with initial conditions
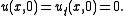
A solution is
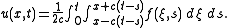
Suppose we have a constant coefficient, mth order inhomogeneous ordinary differential equation
.


where
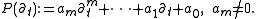
We can reduce this to the solution of a homogeneous ODE using the following method. All steps are done formally, ignoring necessary requirements for the solution to be well defined.
First let G solve
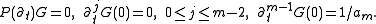
Define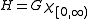 , with
, with 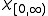 being the characteristic function
being the characteristic function
on the interval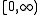 . Then we have
. Then we have
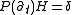
in the sense of distributions
. Therefore
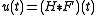
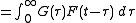
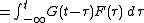
solves the ODE.
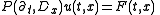
where
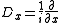
We can reduce this to the solution of a homogeneous ODE using the following method. All steps are done formally, ignoring necessary requirements for the solution to be well defined.
First, taking the Fourier transform
in x we have
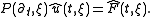
Assume that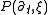 is an mth order ODE in t. Let
is an mth order ODE in t. Let  be the coefficient of the highest order term of
be the coefficient of the highest order term of 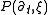 .
.
Now for every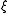 let
let 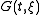 solve
solve
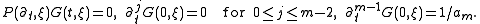
Define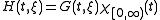 . We then have
. We then have
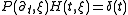
in the sense of distributions
. Therefore
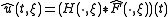
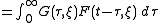
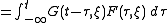
solves the PDE (after transforming back to x).
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, and more specifically in partial differential equations, Duhamel's principle is a general method for obtaining solutions to inhomogeneous
Homogeneous differential equation
The term homogeneous differential equation has several distinct meanings.One meaning is that a first-order ordinary differential equation is homogeneous if it has the formwhere F is a homogeneous function of degree zero; that is to say, that F = F.In a related, but distinct, usage, the term linear...
linear evolution equations like the heat equation
Heat equation
The heat equation is an important partial differential equation which describes the distribution of heat in a given region over time...
, wave equation
Wave equation
The wave equation is an important second-order linear partial differential equation for the description of waves – as they occur in physics – such as sound waves, light waves and water waves. It arises in fields like acoustics, electromagnetics, and fluid dynamics...
, and vibrating plate
Vibrating plate
In solid mechanics, a branch of mathematics and physics, a plate is modeled as a two-dimensional elastic body whose potential energy depends on how it is bent from a planar configuration, rather than how it is stretched . A vibrating plate can be modeled in a manner analogous to a vibrating drum...
equation. It is named for Jean-Marie Duhamel
Jean-Marie Duhamel
Jean-Marie Constant Duhamel was a noted French mathematician and physicist. His studies were affected by troubles of the Napoleonic era. He went on to form his own school École Sainte-Barbe. Duhamel's principle is named for him. He was primarily a mathematician but did studies on the mathematics...
who first applied the principle to the inhomogeneous heat equation that models, for instance, the distribution of heat in a thin plate heated from beneath. For linear evolution equations without spatial dependency, such as a harmonic oscillator
Harmonic oscillator
In classical mechanics, a harmonic oscillator is a system that, when displaced from its equilibrium position, experiences a restoring force, F, proportional to the displacement, x: \vec F = -k \vec x \, where k is a positive constant....
, Duhamel's principle reduces to the method of variation of parameters technique for solving linear inhomogeneous ordinary differential equations.
The philosophy underlying Duhamel's principle is that it is possible to go from solutions of the Cauchy problem
Cauchy problem
A Cauchy problem in mathematics asks for the solution of a partial differential equation that satisfies certain conditions which are given on a hypersurface in the domain. Cauchy problems are an extension of initial value problems and are to be contrasted with boundary value problems...
(or initial value problem) to solutions of the inhomogeneous problem. Consider, for instance, the example of the heat equation modeling the distribution of heat energy u in Rn. The initial value problem is
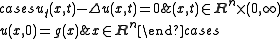
where g is the initial heat distribution. By contrast, the inhomogeneous problem for the heat equation is
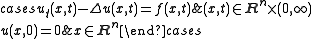
corresponds to adding an external heat energy ƒ(x,t)dt at each point. Intuitively, one can think of the inhomogeneous problem as set of homogeneous problems each starting afresh at a different time slice t = t0. By linearity, one can add up (integrate) the resulting solutions through time t0 and obtain the solution for the inhomogeneous problem. This is the essence of Duhamel's principle.
General considerations
Formally, consider a linear inhomogeneous evolution equation for a function
with spatial domain D in Rn, of the form
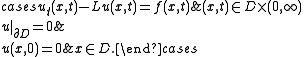
where L is a linear differential operator that involves no time derivatives.
Duhamel's principle is, formally, that the solution to this problem is
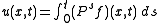
where Psƒ is the solution of the problem
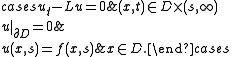
Duhamel's principle also holds for linear systems (with vector-valued functions u), and this in turn furnishes a generalization to higher t derivatives, such as those appearing in the wave equation (see below). Validity of the principle depends on being able to solve the homogeneous problem in an appropriate function space and that the solution should exhibit reasonable dependence on parameters so that the integral is well-defined. Precise analytic conditions on u and f depend on the particular application.
Wave equation
Given the inhomogeneous wave equation: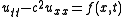
with initial conditions
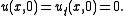
A solution is
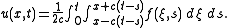
Constant-coefficient linear ODE
Duhamel's principle is the result that the solution to an inhomogeneous, linear, partial differential equation can be solved by first finding the solution for a step input, and then superposing using Duhamel's integral.Suppose we have a constant coefficient, mth order inhomogeneous ordinary differential equation
Ordinary differential equation
In mathematics, an ordinary differential equation is a relation that contains functions of only one independent variable, and one or more of their derivatives with respect to that variable....
.


where
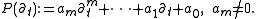
We can reduce this to the solution of a homogeneous ODE using the following method. All steps are done formally, ignoring necessary requirements for the solution to be well defined.
First let G solve
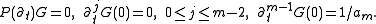
Define
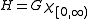 , with
, with 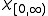 being the characteristic function
being the characteristic functionCharacteristic function
In mathematics, characteristic function can refer to any of several distinct concepts:* The most common and universal usage is as a synonym for indicator function, that is the function* In probability theory, the characteristic function of any probability distribution on the real line is given by...
on the interval
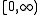 . Then we have
. Then we have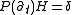
in the sense of distributions
Distribution (mathematics)
In mathematical analysis, distributions are objects that generalize functions. Distributions make it possible to differentiate functions whose derivatives do not exist in the classical sense. In particular, any locally integrable function has a distributional derivative...
. Therefore
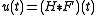
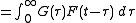
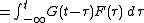
solves the ODE.
Constant-coefficient linear PDE
More generally, suppose we have a constant coefficient inhomogeneous partial differential equationPartial differential equation
In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
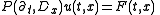
where
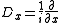
We can reduce this to the solution of a homogeneous ODE using the following method. All steps are done formally, ignoring necessary requirements for the solution to be well defined.
First, taking the Fourier transform
Fourier transform
In mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...
in x we have
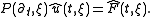
Assume that
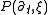 is an mth order ODE in t. Let
is an mth order ODE in t. Let  be the coefficient of the highest order term of
be the coefficient of the highest order term of 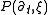 .
.Now for every
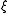 let
let 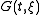 solve
solve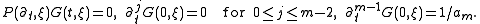
Define
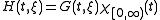 . We then have
. We then have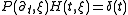
in the sense of distributions
Distribution (mathematics)
In mathematical analysis, distributions are objects that generalize functions. Distributions make it possible to differentiate functions whose derivatives do not exist in the classical sense. In particular, any locally integrable function has a distributional derivative...
. Therefore
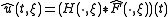
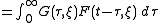
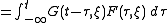
solves the PDE (after transforming back to x).

