Dilworth's theorem
Encyclopedia
In mathematics
, in the areas of order theory
and combinatorics
, Dilworth's theorem characterizes the width of any finite partially ordered set
in terms of a partition
of the order into a minimum number of chains. It is named for the mathematician .
An antichain
in a partially ordered set is a set of elements no two of which are comparable to each other, and a chain is a set of elements every two of which are comparable. Dilworth's theorem states that there exists an antichain A, and a partition of the order into a family P of chains, such that the number of chains in the partition equals the cardinality of A. When this occurs, A must be the largest antichain in the order, for any antichain can have at most one element from each member of P. Similarly, P must be the smallest family of chains into which the order can be partitioned, for any partition into chains must have at least one chain per element of A. The width of the partial order is defined as the common size of A and P.
An equivalent way of stating Dilworth's theorem is that, in any finite partially ordered set, the maximum number of elements in any antichain equals the minimum number of chains in any partition of the set into chains. A version of the theorem for infinite partially ordered sets states that, in this case, a partially ordered set has finite width w if and only if may be partitioned into w chains.
is based on that of .
Let
be a finite partially ordered set. The theorem holds trivially if 
is empty. So, assume that 
has at least one element, and let 
be a maximal element of 
.
By induction, we assume that for some integer
the partially ordered set 
can be covered by 
disjoint chains 
and has at least one antichain 
of size 
. Clearly, 
for 
. For 
, let 
be the maximal element in 
that belongs to an antichain of size 
in 
, and set 
.
We claim that
is an antichain.
Let
be an antichain of size 
that contains 
. Fix arbitrary distinct indices 
and 
. Then 
. Let 
. Then 
, by the definition of 
. This implies that 
, since 
. By interchanging the roles of 
and 
in this argument we also have 
. This verifies that 
is an antichain.
We now return to
. Suppose first that 
for some 
. Let 
be the chain 
. Then by the choice of 
, 
does not have an antichain of size 
. Induction then implies that 
can be covered by 
disjoint chains since 
is an antichain of size 
in 
.
Thus,
can be covered by 
disjoint chains, as required. Next, if 
for each 
, then 
is an antichain of size 
in 
(since 
is maximal in 
). Now 
can be covered by the 
chains 
, completing the proof.
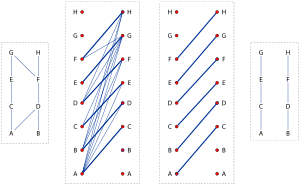Like a number of other results in combinatorics, Dilworth's theorem is equivalent to König's theorem
on bipartite graph
matching and several other related theorems including Hall's Marriage theorem
.
To prove Dilworth's theorem for a partial order S with n elements, using König's theorem, define a bipartite graph G = (U,V,E) where U = V = S and where (u,v) is an edge in G when u < v in S. By König's theorem, there exists a matching M in G, and a set of vertices C in G, such that each edge in the graph contains at least one vertex in C and such that M and C have the same cardinality m. Let A be the set of elements of S that do not correspond to any vertex in C; then A has at least n - m elements (possibly more if C contains vertices corresponding to the same element on both sides of the bipartition). Let P be a family of chains formed by including x and y in the same chain whenever there is an edge (x,y) in M; then P has n - m chains. Therefore, we have constructed an antichain and a partition into chains with the same cardinality.
To prove König's theorem from Dilworth's theorem, for a bipartite graph G = (U,V,E), form a partial order on the vertices of G in which u < v exactly when u is in U, v is in V, and there exists an edge in E from u to v. By Dilworth's theorem, there exists an antichain A and a partition into chains P both of which have the same size. But the only nontrivial chains in the partial order are pairs of elements corresponding to the edges in the graph, so the nontrivial chains in P form a matching in the graph. The complement of A forms a vertex cover in G with the same cardinality as this matching.
This connection to bipartite matching allows the width of any partial order to be computed in polynomial time.
of the incomparability graph
of S (a graph that has the elements of S as vertices, with an edge between every two incomparable elements) using w colors; every color class in a proper coloring of the incomparability graph must be a chain. By the assumption that P has width w, and by the finite version of Dilworth's theorem, every finite subset S of P has a w-colorable incomparability graph. Therefore, by the De Bruijn–Erdős theorem
, P itself also has a w-colorable incomparability graph, and thus has the desired partition into chains .
However, the theorem does not extend so simply to partially ordered sets in which the width, and not just the cardinality of the set, is infinite. In this case the size of the largest antichain and the minimum number of chains needed to cover the partial order may be very different from each other. In particular, for every infinite cardinal number κ there is an infinite partially ordered set in which the largest antichain has size ℵ0 and the partition into the fewest chains has κ chains .
is an undirected graph formed from a partial order by creating a vertex per element of the order, and an edge connecting any two comparable elements. Thus, a clique
in a comparability graph corresponds to a chain, and an independent set
in a comparability graph corresponds to an antichain. Any induced subgraph of a comparability graph is itself a comparability graph, formed from the restriction of the partial order to a subset of its elements.
An undirected graph is perfect
if, in every induced subgraph, the chromatic number equals the size of the largest clique. Every comparability graph is perfect: this is essentially just Mirsky's theorem, restated in graph-theoretic terms . It is known that the complement
of any perfect graph is also perfect . Therefore, the complement of any comparability graph is perfect; this is essentially just Dilworth's theorem itself, restated in graph-theoretic terms . Thus, the complementation property of perfect graphs can provide an alternative proof of Dilworth's theorem.
In other words, a largest family of incomparable subsets of X is obtained by selecting the subsets of X that have median size. The Lubell–Yamamoto–Meshalkin inequality also concerns antichains in a power set and can be used to prove Sperner's theorem.
If we order the integers in the interval [1, 2n] by divisibility, the subinterval [n + 1, 2n] forms an antichain with cardinality n. A partition of this partial order into n chains is easy to achieve: for each odd integer m in [1,2n], form a chain of the numbers of the form m2i. Therefore, by Dilworth's theorem, the width of this partial order is n. Abouabdillah's theorem
characterizes the integers that can belong to maximum antichains in this order.
The Erdős–Szekeres theorem
on monotone subsequences can be interpreted as an application of Dilworth's theorem to partial orders of order dimension
two .
The "convex dimension" of an antimatroid
is defined as the minimum number of chains needed to define the antimatroid, and Dilworth's theorem can be used to show that it equals the width of an associated partial order; this connection leads to a polynomial time algorithm for convex dimension .
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, in the areas of order theory
Order theory
Order theory is a branch of mathematics which investigates our intuitive notion of order using binary relations. It provides a formal framework for describing statements such as "this is less than that" or "this precedes that". This article introduces the field and gives some basic definitions...
and combinatorics
Combinatorics
Combinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size , deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria ,...
, Dilworth's theorem characterizes the width of any finite partially ordered set
Partially ordered set
In mathematics, especially order theory, a partially ordered set formalizes and generalizes the intuitive concept of an ordering, sequencing, or arrangement of the elements of a set. A poset consists of a set together with a binary relation that indicates that, for certain pairs of elements in the...
in terms of a partition
Partition of a set
In mathematics, a partition of a set X is a division of X into non-overlapping and non-empty "parts" or "blocks" or "cells" that cover all of X...
of the order into a minimum number of chains. It is named for the mathematician .
An antichain
Antichain
In mathematics, in the area of order theory, an antichain is a subset of a partially ordered set such that any two elements in the subset are incomparable. Let S be a partially ordered set...
in a partially ordered set is a set of elements no two of which are comparable to each other, and a chain is a set of elements every two of which are comparable. Dilworth's theorem states that there exists an antichain A, and a partition of the order into a family P of chains, such that the number of chains in the partition equals the cardinality of A. When this occurs, A must be the largest antichain in the order, for any antichain can have at most one element from each member of P. Similarly, P must be the smallest family of chains into which the order can be partitioned, for any partition into chains must have at least one chain per element of A. The width of the partial order is defined as the common size of A and P.
An equivalent way of stating Dilworth's theorem is that, in any finite partially ordered set, the maximum number of elements in any antichain equals the minimum number of chains in any partition of the set into chains. A version of the theorem for infinite partially ordered sets states that, in this case, a partially ordered set has finite width w if and only if may be partitioned into w chains.
Inductive proof
The following proof by induction on the size of the partially ordered set is based on that of .Let
be a finite partially ordered set. The theorem holds trivially if is empty. So, assume that has at least one element, and let be a maximal element of .By induction, we assume that for some integer
the partially ordered set can be covered by disjoint chains and has at least one antichain of size . Clearly, for . For , let be the maximal element in that belongs to an antichain of size in , and set .We claim that
is an antichain.Let
be an antichain of size that contains . Fix arbitrary distinct indices and . Then . Let . Then , by the definition of . This implies that , since . By interchanging the roles of and in this argument we also have . This verifies that is an antichain.We now return to
. Suppose first that for some . Let be the chain . Then by the choice of , does not have an antichain of size . Induction then implies that can be covered by disjoint chains since is an antichain of size in .Thus,
can be covered by disjoint chains, as required. Next, if for each , then is an antichain of size in (since is maximal in ). Now can be covered by the chains , completing the proof.Proof via König's theorem
König's theorem (graph theory)
In the mathematical area of graph theory, König's theorem, proved by Dénes Kőnig in 1931, describes an equivalence between the maximum matching problem and the minimum vertex cover problem in bipartite graphs...
on bipartite graph
Bipartite graph
In the mathematical field of graph theory, a bipartite graph is a graph whose vertices can be divided into two disjoint sets U and V such that every edge connects a vertex in U to one in V; that is, U and V are independent sets...
matching and several other related theorems including Hall's Marriage theorem
Marriage theorem
In mathematics, Hall's marriage theorem is a combinatorial result that gives the condition allowing the selection of a distinct element from each of a collection of finite sets...
.
To prove Dilworth's theorem for a partial order S with n elements, using König's theorem, define a bipartite graph G = (U,V,E) where U = V = S and where (u,v) is an edge in G when u < v in S. By König's theorem, there exists a matching M in G, and a set of vertices C in G, such that each edge in the graph contains at least one vertex in C and such that M and C have the same cardinality m. Let A be the set of elements of S that do not correspond to any vertex in C; then A has at least n - m elements (possibly more if C contains vertices corresponding to the same element on both sides of the bipartition). Let P be a family of chains formed by including x and y in the same chain whenever there is an edge (x,y) in M; then P has n - m chains. Therefore, we have constructed an antichain and a partition into chains with the same cardinality.
To prove König's theorem from Dilworth's theorem, for a bipartite graph G = (U,V,E), form a partial order on the vertices of G in which u < v exactly when u is in U, v is in V, and there exists an edge in E from u to v. By Dilworth's theorem, there exists an antichain A and a partition into chains P both of which have the same size. But the only nontrivial chains in the partial order are pairs of elements corresponding to the edges in the graph, so the nontrivial chains in P form a matching in the graph. The complement of A forms a vertex cover in G with the same cardinality as this matching.
This connection to bipartite matching allows the width of any partial order to be computed in polynomial time.
Extension to infinite partially ordered sets
Dilworth's theorem for infinite partially ordered sets states that a partially ordered set has finite width w if and only if may be partitioned into w chains. For, suppose that an infinite partial order P has width w, meaning that there are at most a finite number w of elements in any antichain. For any subset S of P, a decomposition into w chains (if it exists) may be described as a coloringGraph coloring
In graph theory, graph coloring is a special case of graph labeling; it is an assignment of labels traditionally called "colors" to elements of a graph subject to certain constraints. In its simplest form, it is a way of coloring the vertices of a graph such that no two adjacent vertices share the...
of the incomparability graph
Comparability graph
In graph theory, a comparability graph is an undirected graph that connects pairs of elements that are comparable to each other in a partial order...
of S (a graph that has the elements of S as vertices, with an edge between every two incomparable elements) using w colors; every color class in a proper coloring of the incomparability graph must be a chain. By the assumption that P has width w, and by the finite version of Dilworth's theorem, every finite subset S of P has a w-colorable incomparability graph. Therefore, by the De Bruijn–Erdős theorem
De Bruijn–Erdős theorem
In graph theory, the De Bruijn–Erdős theorem, proved by , states that, for every infinite graph and finite integer , can be colored by colors if and only if each of its finite subgraphs can be colored by colors...
, P itself also has a w-colorable incomparability graph, and thus has the desired partition into chains .
However, the theorem does not extend so simply to partially ordered sets in which the width, and not just the cardinality of the set, is infinite. In this case the size of the largest antichain and the minimum number of chains needed to cover the partial order may be very different from each other. In particular, for every infinite cardinal number κ there is an infinite partially ordered set in which the largest antichain has size ℵ0 and the partition into the fewest chains has κ chains .
Dual of Dilworth's theorem (Mirsky's theorem)
A dual of Dilworth's theorem states that the size of the largest chain in a partial order (if finite) equals the smallest number of antichains into which the order may be partitioned . The proof of this is much simpler than the proof of Dilworth's theorem itself: for any element x, consider the chains that have x as their largest element, and let N(x) denote the size of the largest of these x-maximal chains. Then each set N−1(i), consisting of elements that have equal values of N, is an antichain, and these antichains partition the partial order into a number of antichains equal to the size of the largest chain.Perfection of comparability graphs
A comparability graphComparability graph
In graph theory, a comparability graph is an undirected graph that connects pairs of elements that are comparable to each other in a partial order...
is an undirected graph formed from a partial order by creating a vertex per element of the order, and an edge connecting any two comparable elements. Thus, a clique
Clique (graph theory)
In the mathematical area of graph theory, a clique in an undirected graph is a subset of its vertices such that every two vertices in the subset are connected by an edge. Cliques are one of the basic concepts of graph theory and are used in many other mathematical problems and constructions on graphs...
in a comparability graph corresponds to a chain, and an independent set
Independent set (graph theory)
In graph theory, an independent set or stable set is a set of vertices in a graph, no two of which are adjacent. That is, it is a set I of vertices such that for every two vertices in I, there is no edge connecting the two. Equivalently, each edge in the graph has at most one endpoint in I...
in a comparability graph corresponds to an antichain. Any induced subgraph of a comparability graph is itself a comparability graph, formed from the restriction of the partial order to a subset of its elements.
An undirected graph is perfect
Perfect graph
In graph theory, a perfect graph is a graph in which the chromatic number of every induced subgraph equals the size of the largest clique of that subgraph....
if, in every induced subgraph, the chromatic number equals the size of the largest clique. Every comparability graph is perfect: this is essentially just Mirsky's theorem, restated in graph-theoretic terms . It is known that the complement
Complement graph
In graph theory, the complement or inverse of a graph G is a graph H on the same vertices such that two vertices of H are adjacent if and only if they are not adjacent in G. That is, to generate the complement of a graph, one fills in all the missing edges required to form a complete graph, and...
of any perfect graph is also perfect . Therefore, the complement of any comparability graph is perfect; this is essentially just Dilworth's theorem itself, restated in graph-theoretic terms . Thus, the complementation property of perfect graphs can provide an alternative proof of Dilworth's theorem.
Width of special partial orders
The Boolean lattice Bn is the power set of an n-element set X—essentially {1, 2, …, n}—ordered by inclusion. Sperner's theorem states that a maximum antichain of Bn has size at mostIn other words, a largest family of incomparable subsets of X is obtained by selecting the subsets of X that have median size. The Lubell–Yamamoto–Meshalkin inequality also concerns antichains in a power set and can be used to prove Sperner's theorem.
If we order the integers in the interval [1, 2n] by divisibility, the subinterval [n + 1, 2n] forms an antichain with cardinality n. A partition of this partial order into n chains is easy to achieve: for each odd integer m in [1,2n], form a chain of the numbers of the form m2i. Therefore, by Dilworth's theorem, the width of this partial order is n. Abouabdillah's theorem
Abouabdillah's theorem
Abouabdillah's theorem refers to two distinct theorems in mathematics, proven by Moroccan mathematician Driss Abouabdillah: one in geometry and one in number theory.-Geometry:In geometry, similarities of an Euclidean space preserve circles and spheres...
characterizes the integers that can belong to maximum antichains in this order.
The Erdős–Szekeres theorem
Erdos–Szekeres theorem
In mathematics, the Erdős–Szekeres theorem is a finitary result that makes precise one of the corollaries of Ramsey's theorem. While Ramsey's theorem makes it easy to prove that every sequence of distinct real numbers contains either a monotonically increasing infinite subsequence, or a...
on monotone subsequences can be interpreted as an application of Dilworth's theorem to partial orders of order dimension
Order dimension
In mathematics, the dimension of a partially ordered set is the smallest number of total orders the intersection of which gives rise to the partial order....
two .
The "convex dimension" of an antimatroid
Antimatroid
In mathematics, an antimatroid is a formal system that describes processes in which a set is built up by including elements one at a time, and in which an element, once available for inclusion, remains available until it is included...
is defined as the minimum number of chains needed to define the antimatroid, and Dilworth's theorem can be used to show that it equals the width of an associated partial order; this connection leads to a polynomial time algorithm for convex dimension .