Desargues' theorem
Encyclopedia
In projective geometry
, Desargues' theorem, named in honor of Gérard Desargues
, states:
Denote the three vertices of one triangle by a, b, and c, and those of the other by A, B, and C. Axial perspectivity means that lines ab and AB meet in a point, lines ac and AC meet in a second point, and lines bc and BC meet in a third point, and that these three points all lie on a common line called the axis of perspectivity. Central perspectivity means that the three lines Aa, Bb, and Cc are concurrent, at a point called the center of perspectivity.
The result is true in the usual Euclidean plane but special care needs to be taken in exceptional cases, as when a pair of sides are parallel, so that their "point of intersection" recedes to infinity. Mathematically the most satisfying way of resolving the issue of exceptional cases is to "complete" the Euclidean plane to a projective plane
by "adding" points at infinity following Poncelet
.
Desargues's theorem is true for the real projective plane
, for any projective space defined arithmetically from a field
or division ring
, for any projective space of dimension unequal to two, and for any projective space in which Pappus's theorem
holds. However, there are some non-Desarguesian plane
s in which Desargues' theorem is false.
such as the Euclidean plane a similar statement is true, but only if one lists various exceptions involving parallel lines. Desargues' theorem is therefore one of the most basic of simple and intuitive geometric theorems whose natural home is in projective rather than affine space.
if and only if they are in perspective centrally (or, equivalently according to this theorem, in perspective axially). Note that perspective triangles need not be similar
.
Under the standard duality of plane projective geometry
(where points correspond to lines and collinearity of points corresponds to concurrency of lines), the statement of Desargues's theorem is self-dual: axial perspectivity is translated into central perspectivity and vice versa. The Desargues configuration (below) is a self-dual configuration.
s and are the same as the planes that can be given coordinates over a division ring. There are also many non-Desarguesian plane
s where Desargues's theorem does not hold.
Desargues' theorem can be stated as follows:
The points A, B, a, and b are coplanar because of the assumed concurrency of A.a and B.b. Therefore, the lines (A.B) and (a.b) belong to the same plane and must intersect. Further, if the two triangles lie on different planes, then the point (A.B) ∩ (a.b) belongs to both planes. By a symmetric argument, the points (A.C) ∩ (a.c) and (B.C) ∩ (b.c) also exist and belong to the planes of both triangles. Since these two planes intersect in more than one point, their intersection is a line that contains all three points.
This proves Desargues's theorem if the two triangles are not contained in the same plane. If they are in the same plane, Desargues's theorem can be proved by choosing a point not in the plane, using this to lift the triangles out of the plane so that the argument above works, and then projecting back into the plane.
The last step of the proof fails if the projective space has dimension less than 3, as in this case it may not be possible to find a point outside the plane.
Monge's theorem
also asserts that three points lie on a line, and has a proof using the same idea of considering it in three rather than two dimensions and writing the line as an intersection of two planes.
order to prove it. These conditions usually take the form of assuming the existence of sufficiently many collineation
s of a certain type, which in turn leads to showing that the underlying algebraic coordinate system must be a division ring
(skewfield).
states that, if a hexagon AbCaBc is drawn in such a way that vertices a, b, and c lie on a line and vertices A, B, and C lie on a second line, then each two opposite sides of the hexagon lie on two lines that meet in a point and the three points constructed in this way are collinear. A plane in which Pappus's theorem is universally true is called Pappian.
showed that Desargues's theorem can be deduced from three applications of Pappus's theorem .
The converse of this result is not true, that is, not all Desarguesian planes are Pappian. Satisfying Pappus's theorem universally is equivalent to having the underlying coordinate system be commutative. A plane defined over a non-commutative division ring (a division ring that is not a field) would therefore be Desarguesian but not Pappian. However, due to Wedderburn's theorem, which states that all finite division rings are fields, all finite Desarguesian planes are Pappian. There is no known, satisfactory geometric proof of this fact.
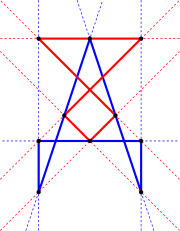The ten lines involved in Desargues' theorem (six sides of triangles, the three lines Aa, Bb, and Cc, and the axis of perspectivity) and the ten points involved (the six vertices, the three points of intersection on the axis of perspectivity, and the center of perspectivity) are so arranged that each of the ten lines passes through three of the ten points, and each of the ten points lies on three of the ten lines. Those ten points and ten lines make up the Desargues configuration, an example of a projective configuration. Although Desargues' theorem chooses different roles for these ten lines and points, the Desargues configuration itself is more symmetric
: any of the ten points may be chosen to be the center of perspectivity, and that choice determines which six points will be the vertices of triangles and which line will be the axis of perspectivity. The Desargues configuration has a symmetry group
of order 120; that is, there are 120 different ways of permuting the points and lines of the configuration in a way that preserves its point-line incidences. One way of constructing the same configuration in a way that makes these symmetries more readily apparent is to choose five planes in three-dimensional space
, and to form the Desargues configuration as the set of ten points where three planes meet and the set of ten lines where two planes meet. Then, the 120 different permutation
s of these five planes each correspond to symmetries of the configuration.
As a projective configuration the Desargues configuration has the notation (103103), meaning that each of its ten points is incident to three lines and each of its ten lines is incident to three points. Its ten points can be viewed in a unique way as a pair of mutually inscribed pentagon
s, or as a self-inscribed decagon
. The Desargues graph
, a 20-vertex bipartite
symmetric
cubic graph
, is so called because it can be interpreted as the Levi graph
of the Desargues configuration, with a vertex for each point and line of the configuration and an edge for every incident point-line pair.
There also exist eight other (103103) configurations (that is, sets of points and lines in the Euclidean plane with three lines per point and three points per line) that are not incidence-isomorphic to the Desargues configuration, one of which is shown at left. In all of these configurations, any chosen point has three other points that are not collinear with it. But in the Desargues configuration, these three points are always collinear with each other (if the chosen point is the center of perspectivity, then the three points form the axis of perspectivity) while in the other configuration shown in the illustration these three points form a triangle of three lines. As with the Desargues configuration, the other depicted configuration can be viewed as a pair of mutually inscribed pentagons.
Projective geometry
In mathematics, projective geometry is the study of geometric properties that are invariant under projective transformations. This means that, compared to elementary geometry, projective geometry has a different setting, projective space, and a selective set of basic geometric concepts...
, Desargues' theorem, named in honor of Gérard Desargues
Gérard Desargues
Girard Desargues was a French mathematician and engineer, who is considered one of the founders of projective geometry. Desargues' theorem, the Desargues graph, and the crater Desargues on the Moon are named in his honour.Born in Lyon, Desargues came from a family devoted to service to the French...
, states:
- Two triangleTriangleA triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted ....
s are in perspective axially if and only ifIf and only ifIn logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
they are in perspective centrally.
Denote the three vertices of one triangle by a, b, and c, and those of the other by A, B, and C. Axial perspectivity means that lines ab and AB meet in a point, lines ac and AC meet in a second point, and lines bc and BC meet in a third point, and that these three points all lie on a common line called the axis of perspectivity. Central perspectivity means that the three lines Aa, Bb, and Cc are concurrent, at a point called the center of perspectivity.
The result is true in the usual Euclidean plane but special care needs to be taken in exceptional cases, as when a pair of sides are parallel, so that their "point of intersection" recedes to infinity. Mathematically the most satisfying way of resolving the issue of exceptional cases is to "complete" the Euclidean plane to a projective plane
Projective plane
In mathematics, a projective plane is a geometric structure that extends the concept of a plane. In the ordinary Euclidean plane, two lines typically intersect in a single point, but there are some pairs of lines that do not intersect...
by "adding" points at infinity following Poncelet
Jean-Victor Poncelet
Jean-Victor Poncelet was a French engineer and mathematician who served most notably as the commandant general of the École Polytechnique...
.
Desargues's theorem is true for the real projective plane
Real projective plane
In mathematics, the real projective plane is an example of a compact non-orientable two-dimensional manifold, that is, a one-sided surface. It cannot be embedded in our usual three-dimensional space without intersecting itself...
, for any projective space defined arithmetically from a field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
or division ring
Division ring
In abstract algebra, a division ring, also called a skew field, is a ring in which division is possible. Specifically, it is a non-trivial ring in which every non-zero element a has a multiplicative inverse, i.e., an element x with...
, for any projective space of dimension unequal to two, and for any projective space in which Pappus's theorem
Pappus's hexagon theorem
In mathematics, Pappus's hexagon theorem states that given one set of collinear points A, B, C, and another set of collinear points a, b, c, then the intersection points X, Y, Z of line pairs Ab and aB, Ac and aC, Bc and bC are collinear...
holds. However, there are some non-Desarguesian plane
Non-Desarguesian plane
In mathematics, a non-Desarguesian plane, named after Gérard Desargues, is a projective plane that does not satisfy Desargues's theorem, or in other words a plane that is not a Desarguesian plane...
s in which Desargues' theorem is false.
Projective versus affine spaces
In an affine spaceAffine space
In mathematics, an affine space is a geometric structure that generalizes the affine properties of Euclidean space. In an affine space, one can subtract points to get vectors, or add a vector to a point to get another point, but one cannot add points. In particular, there is no distinguished point...
such as the Euclidean plane a similar statement is true, but only if one lists various exceptions involving parallel lines. Desargues' theorem is therefore one of the most basic of simple and intuitive geometric theorems whose natural home is in projective rather than affine space.
Self-duality
By definition, two triangles are perspectivePerspective (geometry)
In geometry, two triangles are perspective if, when the sides of each triangle are extended, they meet at three collinear points. The line which goes through the three points is known as the perspectrix, perspective axis, homology axis, or axis of perspectivity. The triangles are said to be...
if and only if they are in perspective centrally (or, equivalently according to this theorem, in perspective axially). Note that perspective triangles need not be similar
Similarity (geometry)
Two geometrical objects are called similar if they both have the same shape. More precisely, either one is congruent to the result of a uniform scaling of the other...
.
Under the standard duality of plane projective geometry
Duality (projective geometry)
A striking feature of projective planes is the "symmetry" of the roles played by points and lines in the definitions and theorems, and duality is the formalization of this metamathematical concept. There are two approaches to the subject of duality, one through language and the other a more...
(where points correspond to lines and collinearity of points corresponds to concurrency of lines), the statement of Desargues's theorem is self-dual: axial perspectivity is translated into central perspectivity and vice versa. The Desargues configuration (below) is a self-dual configuration.
Proof of Desargues' theorem
Desargues's theorem holds for projective space of any dimension over any field or division ring, and also holds for abstract projective spaces of dimension at least 3. In dimension 2 the planes for which it holds are called Desarguesian planeDesarguesian plane
In projective geometry a Desarguesian plane, named after Gérard Desargues, is a plane in which Desargues' theorem holds. The ordinary real projective plane is a Desarguesian plane. More generally any projective plane over a division ring is Desarguesian, and conversely Hilbert showed that any...
s and are the same as the planes that can be given coordinates over a division ring. There are also many non-Desarguesian plane
Non-Desarguesian plane
In mathematics, a non-Desarguesian plane, named after Gérard Desargues, is a projective plane that does not satisfy Desargues's theorem, or in other words a plane that is not a Desarguesian plane...
s where Desargues's theorem does not hold.
Three-dimensional proof
Desargues's theorem is true for any projective space of dimension at least 3, and more generally for any projective space that can be embedded in a space of dimension at least 3.Desargues' theorem can be stated as follows:
- If A.a, B.b, C.c are concurrent, then ∩ (a.b), (A.C) ∩ (a.c), (B.C) ∩ (b.c) are collinear.
The points A, B, a, and b are coplanar because of the assumed concurrency of A.a and B.b. Therefore, the lines (A.B) and (a.b) belong to the same plane and must intersect. Further, if the two triangles lie on different planes, then the point (A.B) ∩ (a.b) belongs to both planes. By a symmetric argument, the points (A.C) ∩ (a.c) and (B.C) ∩ (b.c) also exist and belong to the planes of both triangles. Since these two planes intersect in more than one point, their intersection is a line that contains all three points.
This proves Desargues's theorem if the two triangles are not contained in the same plane. If they are in the same plane, Desargues's theorem can be proved by choosing a point not in the plane, using this to lift the triangles out of the plane so that the argument above works, and then projecting back into the plane.
The last step of the proof fails if the projective space has dimension less than 3, as in this case it may not be possible to find a point outside the plane.
Monge's theorem
Monge's theorem
In geometry, Monge's theorem, named after Gaspard Monge, states that for any three circles in a plane, none of which is inside one of the others, the three intersection points of the three pairs of external tangent lines are in fact collinear....
also asserts that three points lie on a line, and has a proof using the same idea of considering it in three rather than two dimensions and writing the line as an intersection of two planes.
Two-dimensional proof
As there are non-Desarguesian projective planes in which Desargues' theorem is not true, some extra conditions need to be met inorder to prove it. These conditions usually take the form of assuming the existence of sufficiently many collineation
Collineation
In projective geometry, a collineation is a one-to-one and onto map from one projective space to another, or from a projective space to itself, such that the images of collinear points are themselves collinear. All projective linear transformations induce a collineation...
s of a certain type, which in turn leads to showing that the underlying algebraic coordinate system must be a division ring
Division ring
In abstract algebra, a division ring, also called a skew field, is a ring in which division is possible. Specifically, it is a non-trivial ring in which every non-zero element a has a multiplicative inverse, i.e., an element x with...
(skewfield).
Relation to Pappus' theorem
Pappus's hexagon theoremPappus's hexagon theorem
In mathematics, Pappus's hexagon theorem states that given one set of collinear points A, B, C, and another set of collinear points a, b, c, then the intersection points X, Y, Z of line pairs Ab and aB, Ac and aC, Bc and bC are collinear...
states that, if a hexagon AbCaBc is drawn in such a way that vertices a, b, and c lie on a line and vertices A, B, and C lie on a second line, then each two opposite sides of the hexagon lie on two lines that meet in a point and the three points constructed in this way are collinear. A plane in which Pappus's theorem is universally true is called Pappian.
showed that Desargues's theorem can be deduced from three applications of Pappus's theorem .
The converse of this result is not true, that is, not all Desarguesian planes are Pappian. Satisfying Pappus's theorem universally is equivalent to having the underlying coordinate system be commutative. A plane defined over a non-commutative division ring (a division ring that is not a field) would therefore be Desarguesian but not Pappian. However, due to Wedderburn's theorem, which states that all finite division rings are fields, all finite Desarguesian planes are Pappian. There is no known, satisfactory geometric proof of this fact.
The Desargues configuration
Symmetry
Symmetry generally conveys two primary meanings. The first is an imprecise sense of harmonious or aesthetically pleasing proportionality and balance; such that it reflects beauty or perfection...
: any of the ten points may be chosen to be the center of perspectivity, and that choice determines which six points will be the vertices of triangles and which line will be the axis of perspectivity. The Desargues configuration has a symmetry group
Symmetry group
The symmetry group of an object is the group of all isometries under which it is invariant with composition as the operation...
of order 120; that is, there are 120 different ways of permuting the points and lines of the configuration in a way that preserves its point-line incidences. One way of constructing the same configuration in a way that makes these symmetries more readily apparent is to choose five planes in three-dimensional space
Three-dimensional space
Three-dimensional space is a geometric 3-parameters model of the physical universe in which we live. These three dimensions are commonly called length, width, and depth , although any three directions can be chosen, provided that they do not lie in the same plane.In physics and mathematics, a...
, and to form the Desargues configuration as the set of ten points where three planes meet and the set of ten lines where two planes meet. Then, the 120 different permutation
Permutation
In mathematics, the notion of permutation is used with several slightly different meanings, all related to the act of permuting objects or values. Informally, a permutation of a set of objects is an arrangement of those objects into a particular order...
s of these five planes each correspond to symmetries of the configuration.
As a projective configuration the Desargues configuration has the notation (103103), meaning that each of its ten points is incident to three lines and each of its ten lines is incident to three points. Its ten points can be viewed in a unique way as a pair of mutually inscribed pentagon
Pentagon
In geometry, a pentagon is any five-sided polygon. A pentagon may be simple or self-intersecting. The sum of the internal angles in a simple pentagon is 540°. A pentagram is an example of a self-intersecting pentagon.- Regular pentagons :In a regular pentagon, all sides are equal in length and...
s, or as a self-inscribed decagon
Decagon
In geometry, a decagon is any polygon with ten sides and ten angles, and usually refers to a regular decagon, having all sides of equal length and each internal angle equal to 144°...
. The Desargues graph
Desargues graph
In the mathematical field of graph theory, the Desargues graph is a distance-transitive cubic graph with 20 vertices and 30 edges. It is named after Gérard Desargues, arises from several different combinatorial constructions, has a high level of symmetry, is the only known non-planar cubic partial...
, a 20-vertex bipartite
Bipartite graph
In the mathematical field of graph theory, a bipartite graph is a graph whose vertices can be divided into two disjoint sets U and V such that every edge connects a vertex in U to one in V; that is, U and V are independent sets...
symmetric
Symmetric graph
In the mathematical field of graph theory, a graph G is symmetric if, given any two pairs of adjacent vertices u1—v1 and u2—v2 of G, there is an automorphismsuch that...
cubic graph
Cubic graph
In the mathematical field of graph theory, a cubic graph is a graph in which all vertices have degree three. In other words a cubic graph is a 3-regular graph. Cubic graphs are also called trivalent graphs....
, is so called because it can be interpreted as the Levi graph
Levi graph
In combinatorial mathematics, a Levi graph or incidence graph is a bipartite graph associated with an incidence structure. From a collection of points and lines in an incidence geometry or a projective configuration, we form a graph with one vertex per point, one vertex per line, and an edge for...
of the Desargues configuration, with a vertex for each point and line of the configuration and an edge for every incident point-line pair.
External links
- Desargues Theorem at MathWorldMathWorldMathWorld is an online mathematics reference work, created and largely written by Eric W. Weisstein. It is sponsored by and licensed to Wolfram Research, Inc. and was partially funded by the National Science Foundation's National Science Digital Library grant to the University of Illinois at...
- Desargues' Theorem at cut-the-knotCut-the-knotCut-the-knot is a free, advertisement-funded educational website maintained by Alexander Bogomolny and devoted to popular exposition of many topics in mathematics. The site has won more than 20 awards from scientific and educational publications, including a Scientific American Web Award in 2003,...
- Monge via Desargues at cut-the-knotCut-the-knotCut-the-knot is a free, advertisement-funded educational website maintained by Alexander Bogomolny and devoted to popular exposition of many topics in mathematics. The site has won more than 20 awards from scientific and educational publications, including a Scientific American Web Award in 2003,...
- Alternate proof of Desargues' theorem at PlanetMathPlanetMathPlanetMath is a free, collaborative, online mathematics encyclopedia. The emphasis is on rigour, openness, pedagogy, real-time content, interlinked content, and also community of about 24,000 people with various maths interests. Intended to be comprehensive, the project is hosted by the Digital...
- Desargues' Theorem at Dynamic Geometry Sketches