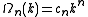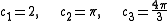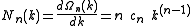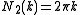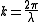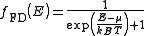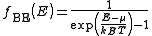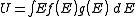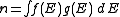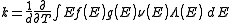
Density of states
Encyclopedia
In solid-state
and condensed matter physics
, the density of states (DOS) of a system describes the number of states per interval of energy at each energy level that are available to be occupied by electrons. Unlike isolated systems, like atoms or molecules in gas phase, the density distributions are not discrete like a spectral density
but continuous. A high DOS at a specific energy level means that there are many states available for occupation. A DOS of zero means that no states can be occupied at that energy level. In general a DOS is an average over the space and time domains occupied by the system. Local
variations, most often due to distortions of the original system, are often called local density of states (LDOS). If the DOS of an undisturbed
system is zero, the LDOS can locally be non-zero due to the presence of a local potential.
metals (examples of degenerate matter
and a Fermi gas
), have a 3-dimensional Euclidean topology
. Less familiar systems, like 2-dimensional electron
gases (2DEG
) in graphite
layers and the Quantum Hall effect system in MOSFET
type devices,
have a 2-dimensional Euclidean topology. Even less familiar are Carbon nanotubes, the quantum wire
and Luttinger liquid
with their 1-dimensional topologies. The topological properties of the system have a major impact on the properties of the density of states. Systems with 1D and 2D topologies are likely to become more common, assuming developments in nanotechnology
and materials science
proceed.
Waves in a QM system have specific wavelengths and can propagate in specific directions, and each wave occupies a different mode, or state. Because many of these states have the same wavelength, and therefore share the same energy, there may be many states available at certain energy levels, while no states are available at other energy levels.
For example, the density of states for electrons in a semiconductor is shown in red in Fig. 4. For electrons at the conduction band edge, very few states are available for the electron to occupy. As the electron increases in energy, the electron density of states increases and more states become available for occupation. However, because there are no states available for electrons to occupy within the bandgap, electrons at the conduction band edge must lose at least
of energy in order to transition to another available mode.
The density of states can be calculated for electron
, photon
, or phonon
in QM systems. The DOS is usually represented by one of the symbols g, ρ, D, n, or N, and can be given as a function of either energy or wave vector
k. To convert between energy and wave vector, the specific relation between E and k must be known.
.svg.png)
There are a large variety of systems and types of states for which DOS calculations can be done. An important property of a condensed matter system is the symmetry
of the structure
on its microscopic scale. Fluid
s, glass
es or amorphous solid
s have dispersion relations with a rotational symmetry. In spherically symmetric systems the integrals of functions, for instance, are one-dimensional because all variables in the calculation depend only on the radial parameter of the dispersion relation.
Angular dependent calculations or measurements on a systems consisting of a single crystal
of a compound, for example, are not anisotropic. The DOS in such cases is often called a projected density of states. Evaluation and calculation of functions and integrals are done on fixed points and in a certain direction and along certain lines or planes through the anisotropic dispersion relations of the system.
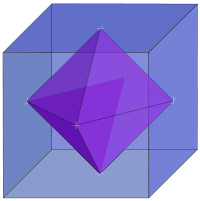Measurements on powders or polycrystalline samples require evaluation and calculation functions and integrals over the whole domain, most often a Brillouin zone
, of the dispersion relations the system of interest. Sometimes the symmetry of the system is high. The shape of the functions describing the dispersion relations of the system appears many times over the whole domain of the dispersion relation. In such cases the effort to calculate the DOS can be reduced by a great amount when the calculation is limited to a reduced zone or
fundamental domain
. The Brillouin zone of the FCC lattice in the figure on the right has the 48 fold symmetry of the point group
Oh with full octahedral symmetry. This means that the integration over the whole domain of the Brillouin zone can be reduced to a 48-th part of the whole Brillouin zone. As a crystal structure periodic table
shows, there are many elements with a FCC crystal structure, like Diamond
, Silicon
and Platinum
and their Brillouin zones and dispersion relations have this 48 fold symmetry.
Two other familiar crystal structures are the BCC and HCP structures with cubic and hexagonal lattices. The BCC structure has the 24 fold pyritohedral symmetry of the point group Th. The HCP structure has the 12 fold prismatic dihedral symmetry of the point group D3h. A complete list of symmetry properties of a point group can be found in point group character tables.
In general it is easier to calculate a DOS when the symmetry of the system is higher and the number of topological dimensions of the dispersion relation is lower. The DOS of dispersion relations with rotational symmetry can often be calculated analytically. In this respect nature is at the hand of calculating and analyzing man because systems with high symmetry are thermodynamically
favorable over systems with lower symmetry.
This is because the entropy
of a system of higher symmetry, like the case of a higher so called multiplicity
, is also higher. The thermally excited particles in the system, with some arbitrary energy in a partially filled band, can be distributed over more available states. There are more possible ways to distribute them because there are more states available what results in a higher entropy.
The density of states is dependent upon the dimensional limits of the object itself. The role dimensions play is evident from the units of DOS (Energy−1Volume−1). In the limit that the system is 2 dimensional a volume becomes an area and in the limit of 1 dimension it becomes a length. It is important to note that the volume being referenced is the volume of k-space, the space enclosed by the constant energy surface of the system derived through a dispersion relation
that relates E to k. The dispersion relation for electrons in a solid is given by the
electronic band structure
.
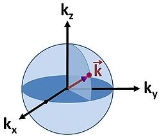
An example of a 3-dimensional k-space is given in Fig. 1. It can be seen that the dimensionality of the system itself will confine the momentum of particles inside the system.
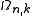
in n-dimensions at an arbitrary k, with respect to k. The volume, area or length in 3, 2 or 1-dimensional k-spaces are expressed by
for a n-dimensional k-space with the topologically determined constants
for linear, disk and spherical symmetrical shaped functions in 1, 2 and 3-dimensional Euclidian k-spaces respectively.
According to this scheme the density of wave vector states N is, by differentiating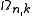
with respect to k, expressed by
The 1, 2 and 3-dimensional density of wave vector states are explicitly written as
One state is large enough to contain particles having wavelength λ. The wavelength is related to k through the relationship.
In a quantum system the length of λ will depend on a characteristic spacing of the system L that is confining the particles. Finally the density of
states N is multiplied by a factor s,
where s is a constant degeneracy factor that accounts for internal degrees of freedom due to such physical phenomena as spin or polarization. If no such phenomenon is present then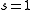
. Vk is the volume in k-space containing all states whose wavevectors are smaller than a certain k serving as a parameter.
inside an interval 
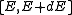. The general form of DOS of a system is given as
The scheme sketched so far only applies to continuously rising and spherically symmetric dispersion relations. In general the dispersion relation
is not spherically symmetric and in many cases it isn't continuously rising either. To express D as a function of E the inverse of the dispersion relation
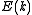has to be substituted into the expression of 
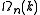as a function of k to get the expression of 
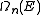as a function of the energy. If the dispersion relation is not spherically symmetric or continuously rising and can't be inverted easily then in most cases the DOS has to be calculated numerically. More detailed derivations are available.
of a particle depends on the magnitude and direction of the wave vector
k, the properties of the particle
and the environment in which the particle is moving.
For example, the kinetic energy of an electron
in a Fermi gas
is given by
where m is the electron mass. The dispersion relation is a spherically symmetric parabola and it is continuously rising so the DOS can be calculated easily.
For longitudinal phonon
s in a string of atoms the dispersion relation of the kinetic energy in a 1-dimensional k-space, as shown in Figure 2, is given by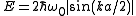
where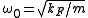
is the oscillator frequency, 
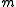the mass of the atoms, 
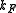the inter-atomic force constant and 
inter-atomic spacing. For small values of 
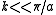the dispersion relation is rather linear: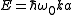
When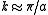
the energy is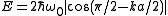
With the transformation
and small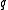 
this relation can be transformed to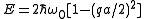
This is a kind of dispersion relation
because it interrelates two wave properties and it is isotropic
because only the length and not the direction of the wave vector appears in the expression.
The magnitude of the wave vector is related to the energy as:
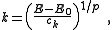
Accordingly, the volume of n-dimensional k-space containing wave vectors smaller than k is:
Substitution of the isotropic energy relation gives the volume of occupied states
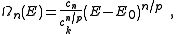
Differentiating this volume with respect to the energy gives an expression for the DOS of the isotopic dispersion relation
resulting density of states,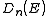
, for electrons in a n-dimensional systems is
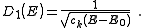
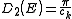
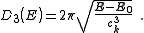
In 1-dimensional systems the DOS diverges at the bottom of the band as
drops to 
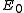. In 2-dimensional systems the DOS turns
out to be independent of
. Finally for 3-dimensional systems the DOS rises as the square root of the energy.
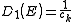
Fermi-Dirac statistics
: The Fermi-Dirac probability distribution function, Fig. 4, is used to find the probability that a fermion occupies a specific quantum state in a system at thermal equilibrium. Fermions are particles which obey the Pauli Exclusion Principle
(e.g. electrons, protons, neutrons). The distribution function can be written as
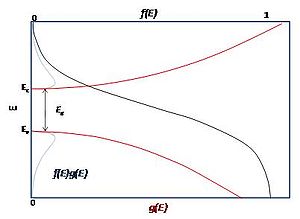
is the chemical potential
(also denoted as EF and called the Fermi level
),
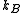is the Boltzmann constant, and 
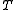is temperature. Fig. 4 illustrates how the product of the Fermi-Dirac distribution function and the three dimensional density of states for a semiconductor can give insight to physical properties such as carrier concentration and Energy band gaps.
Bose-Einstein statistics: The Bose-Einstein probability distribution function is used to find the probability that a boson occupies a specific quantum state in a system at thermal equilibrium. Bosons are particles which do not obey the Pauli Exclusion Principle (e.g. phonons and photons). The distribution function can be written as
From these two distributions it is possible to calculate properties such as the internal energy
, the density of particles 
, specific heat capacity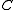 
, and thermal conductivity
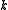. The relationships between these properties and the product of the density of states and the probability distribution, denoting the density of states by 
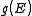instead of 
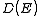, are given by
is dimensionality, 
is sound velocity and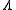 
is mean free path
.
Computer simulations offer a set of algorithms to evaluate the density of states with a high accuracy. One of these
algorithms is called the Wang and Landau algorithm
.
Within the Wang and Landau scheme any previous knowledge of the density of states is required. One proceed as follows:
the cost function (for example the energy) of the system is discretized. Each time the bin i is reached one update
a histogram for the density of, states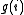
,by,
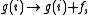
where f is called modification factor. As soon as each bin in the histogram is visited a certain number of times
(10-15), the modification factor is reduced by some criterion, for instance,
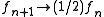
where n denotes the n-th update step. The simulation finishes when the modification factor is less than a certain threshold, for instance
.
The Wang and Landau algorithm has some advantages over other common algorithms such as multicanonical simulations and
Parallel tempering
, for instance, the density of states is obtained as the main product of the simulation.
Additionally, Wang and Landau simulations are completely independent of the temperature. This feature allows to compute the density of states of systems with very rough energy landscape such as proteins.
Solid-state physics
Solid-state physics is the study of rigid matter, or solids, through methods such as quantum mechanics, crystallography, electromagnetism, and metallurgy. It is the largest branch of condensed matter physics. Solid-state physics studies how the large-scale properties of solid materials result from...
and condensed matter physics
Condensed matter physics
Condensed matter physics deals with the physical properties of condensed phases of matter. These properties appear when a number of atoms at the supramolecular and macromolecular scale interact strongly and adhere to each other or are otherwise highly concentrated in a system. The most familiar...
, the density of states (DOS) of a system describes the number of states per interval of energy at each energy level that are available to be occupied by electrons. Unlike isolated systems, like atoms or molecules in gas phase, the density distributions are not discrete like a spectral density
Spectral density
In statistical signal processing and physics, the spectral density, power spectral density , or energy spectral density , is a positive real function of a frequency variable associated with a stationary stochastic process, or a deterministic function of time, which has dimensions of power per hertz...
but continuous. A high DOS at a specific energy level means that there are many states available for occupation. A DOS of zero means that no states can be occupied at that energy level. In general a DOS is an average over the space and time domains occupied by the system. Local
variations, most often due to distortions of the original system, are often called local density of states (LDOS). If the DOS of an undisturbed
system is zero, the LDOS can locally be non-zero due to the presence of a local potential.
Introduction
In quantum mechanical (QM) systems, not all waves, or wave-like particles, are allowed to exist. In some systems, the interatomic spacing and the atomic charge of the material allows only electrons of certain wavelengths to exist. In other systems, the crystalline structure of the material allows waves to propagate in one direction, while suppressing wave propagation in another direction. The most familiar systems, like neutronium in neutron stars and free electron gases inmetals (examples of degenerate matter
Degenerate matter
Degenerate matter is matter that has such extraordinarily high density that the dominant contribution to its pressure is attributable to the Pauli exclusion principle. The pressure maintained by a body of degenerate matter is called the degeneracy pressure, and arises because the Pauli principle...
and a Fermi gas
Fermi gas
A Fermi gas is an ensemble of a large number of fermions. Fermions, named after Enrico Fermi, are particles that obey Fermi–Dirac statistics. These statistics determine the energy distribution of fermions in a Fermi gas in thermal equilibrium, and is characterized by their number density,...
), have a 3-dimensional Euclidean topology
Euclidean topology
In mathematics, and especially general topology, the Euclidean topology is an example of a topology given to the set of real numbers, denoted by R...
. Less familiar systems, like 2-dimensional electron
gases (2DEG
2DEG
A two-dimensional electron gas is a gas of electrons free to move in two dimensions, but tightly confined in the third. This tight confinement leads to quantized energy levels for motion in that direction, which can then be ignored for most problems. Thus the electrons appear to be a 2D sheet...
) in graphite
Graphite
The mineral graphite is one of the allotropes of carbon. It was named by Abraham Gottlob Werner in 1789 from the Ancient Greek γράφω , "to draw/write", for its use in pencils, where it is commonly called lead . Unlike diamond , graphite is an electrical conductor, a semimetal...
layers and the Quantum Hall effect system in MOSFET
MOSFET
The metal–oxide–semiconductor field-effect transistor is a transistor used for amplifying or switching electronic signals. The basic principle of this kind of transistor was first patented by Julius Edgar Lilienfeld in 1925...
type devices,
have a 2-dimensional Euclidean topology. Even less familiar are Carbon nanotubes, the quantum wire
Quantum wire
In condensed matter physics, a quantum wire is an electrically conducting wire, in which quantum effects are affecting transport properties. Due to the quantum confinement of conduction electrons in the transverse direction of the wire, their transverse energy is quantized into a series of...
and Luttinger liquid
Luttinger liquid
A Tomonaga-Luttinger liquid, more often referred to as simply a Luttinger liquid, is a theoretical model describing interacting electrons in a one-dimensional conductor...
with their 1-dimensional topologies. The topological properties of the system have a major impact on the properties of the density of states. Systems with 1D and 2D topologies are likely to become more common, assuming developments in nanotechnology
Nanotechnology
Nanotechnology is the study of manipulating matter on an atomic and molecular scale. Generally, nanotechnology deals with developing materials, devices, or other structures possessing at least one dimension sized from 1 to 100 nanometres...
and materials science
Materials science
Materials science is an interdisciplinary field applying the properties of matter to various areas of science and engineering. This scientific field investigates the relationship between the structure of materials at atomic or molecular scales and their macroscopic properties. It incorporates...
proceed.
Waves in a QM system have specific wavelengths and can propagate in specific directions, and each wave occupies a different mode, or state. Because many of these states have the same wavelength, and therefore share the same energy, there may be many states available at certain energy levels, while no states are available at other energy levels.
For example, the density of states for electrons in a semiconductor is shown in red in Fig. 4. For electrons at the conduction band edge, very few states are available for the electron to occupy. As the electron increases in energy, the electron density of states increases and more states become available for occupation. However, because there are no states available for electrons to occupy within the bandgap, electrons at the conduction band edge must lose at least
of energy in order to transition to another available mode.The density of states can be calculated for electron
Electron
The electron is a subatomic particle with a negative elementary electric charge. It has no known components or substructure; in other words, it is generally thought to be an elementary particle. An electron has a mass that is approximately 1/1836 that of the proton...
, photon
Photon
In physics, a photon is an elementary particle, the quantum of the electromagnetic interaction and the basic unit of light and all other forms of electromagnetic radiation. It is also the force carrier for the electromagnetic force...
, or phonon
Phonon
In physics, a phonon is a collective excitation in a periodic, elastic arrangement of atoms or molecules in condensed matter, such as solids and some liquids...
in QM systems. The DOS is usually represented by one of the symbols g, ρ, D, n, or N, and can be given as a function of either energy or wave vector
Wave vector
In physics, a wave vector is a vector which helps describe a wave. Like any vector, it has a magnitude and direction, both of which are important: Its magnitude is either the wavenumber or angular wavenumber of the wave , and its direction is ordinarily the direction of wave propagation In...
k. To convert between energy and wave vector, the specific relation between E and k must be known.
Symmetry and density of states
Symmetry
Symmetry generally conveys two primary meanings. The first is an imprecise sense of harmonious or aesthetically pleasing proportionality and balance; such that it reflects beauty or perfection...
of the structure
Crystal structure
In mineralogy and crystallography, crystal structure is a unique arrangement of atoms or molecules in a crystalline liquid or solid. A crystal structure is composed of a pattern, a set of atoms arranged in a particular way, and a lattice exhibiting long-range order and symmetry...
on its microscopic scale. Fluid
Fluid
In physics, a fluid is a substance that continually deforms under an applied shear stress. Fluids are a subset of the phases of matter and include liquids, gases, plasmas and, to some extent, plastic solids....
s, glass
Glass
Glass is an amorphous solid material. Glasses are typically brittle and optically transparent.The most familiar type of glass, used for centuries in windows and drinking vessels, is soda-lime glass, composed of about 75% silica plus Na2O, CaO, and several minor additives...
es or amorphous solid
Amorphous solid
In condensed matter physics, an amorphous or non-crystalline solid is a solid that lacks the long-range order characteristic of a crystal....
s have dispersion relations with a rotational symmetry. In spherically symmetric systems the integrals of functions, for instance, are one-dimensional because all variables in the calculation depend only on the radial parameter of the dispersion relation.
Angular dependent calculations or measurements on a systems consisting of a single crystal
Single crystal
A single crystal or monocrystalline solid is a material in which the crystal lattice of the entire sample is continuous and unbroken to the edges of the sample, with no grain boundaries...
of a compound, for example, are not anisotropic. The DOS in such cases is often called a projected density of states. Evaluation and calculation of functions and integrals are done on fixed points and in a certain direction and along certain lines or planes through the anisotropic dispersion relations of the system.
Brillouin zone
In mathematics and solid state physics, the first Brillouin zone is a uniquely defined primitive cell in reciprocal space. The boundaries of this cell are given by planes related to points on the reciprocal lattice. It is found by the same method as for the Wigner–Seitz cell in the Bravais lattice...
, of the dispersion relations the system of interest. Sometimes the symmetry of the system is high. The shape of the functions describing the dispersion relations of the system appears many times over the whole domain of the dispersion relation. In such cases the effort to calculate the DOS can be reduced by a great amount when the calculation is limited to a reduced zone or
fundamental domain
Fundamental domain
In geometry, the fundamental domain of a symmetry group of an object is a part or pattern, as small or irredundant as possible, which determines the whole object based on the symmetry. More rigorously, given a topological space and a group acting on it, the images of a single point under the group...
. The Brillouin zone of the FCC lattice in the figure on the right has the 48 fold symmetry of the point group
Point groups in three dimensions
In geometry, a point group in three dimensions is an isometry group in three dimensions that leaves the origin fixed, or correspondingly, an isometry group of a sphere. It is a subgroup of the orthogonal group O, the group of all isometries that leave the origin fixed, or correspondingly, the group...
Oh with full octahedral symmetry. This means that the integration over the whole domain of the Brillouin zone can be reduced to a 48-th part of the whole Brillouin zone. As a crystal structure periodic table
Periodic table (crystal structure)
The structures of metallic elements adopted at standard temperatures and pressures are color coded and shown below, the only exception is mercury, Hg, which is a liquid and the structure refers to the low temperature form. The melting points of the metals is shown above the element symbol...
shows, there are many elements with a FCC crystal structure, like Diamond
Diamond
In mineralogy, diamond is an allotrope of carbon, where the carbon atoms are arranged in a variation of the face-centered cubic crystal structure called a diamond lattice. Diamond is less stable than graphite, but the conversion rate from diamond to graphite is negligible at ambient conditions...
, Silicon
Silicon
Silicon is a chemical element with the symbol Si and atomic number 14. A tetravalent metalloid, it is less reactive than its chemical analog carbon, the nonmetal directly above it in the periodic table, but more reactive than germanium, the metalloid directly below it in the table...
and Platinum
Platinum
Platinum is a chemical element with the chemical symbol Pt and an atomic number of 78. Its name is derived from the Spanish term platina del Pinto, which is literally translated into "little silver of the Pinto River." It is a dense, malleable, ductile, precious, gray-white transition metal...
and their Brillouin zones and dispersion relations have this 48 fold symmetry.
Two other familiar crystal structures are the BCC and HCP structures with cubic and hexagonal lattices. The BCC structure has the 24 fold pyritohedral symmetry of the point group Th. The HCP structure has the 12 fold prismatic dihedral symmetry of the point group D3h. A complete list of symmetry properties of a point group can be found in point group character tables.
In general it is easier to calculate a DOS when the symmetry of the system is higher and the number of topological dimensions of the dispersion relation is lower. The DOS of dispersion relations with rotational symmetry can often be calculated analytically. In this respect nature is at the hand of calculating and analyzing man because systems with high symmetry are thermodynamically
Second law of thermodynamics
The second law of thermodynamics is an expression of the tendency that over time, differences in temperature, pressure, and chemical potential equilibrate in an isolated physical system. From the state of thermodynamic equilibrium, the law deduced the principle of the increase of entropy and...
favorable over systems with lower symmetry.
This is because the entropy
Entropy
Entropy is a thermodynamic property that can be used to determine the energy available for useful work in a thermodynamic process, such as in energy conversion devices, engines, or machines. Such devices can only be driven by convertible energy, and have a theoretical maximum efficiency when...
of a system of higher symmetry, like the case of a higher so called multiplicity
Multiplicity (chemistry)
Multiplicity in quantum chemistry is used to distinguish between several degenerate wavefunctions that differ only in the orientation of their angular spin momenta. It is defined as 2S+1, where S is the angular spin momentum....
, is also higher. The thermally excited particles in the system, with some arbitrary energy in a partially filled band, can be distributed over more available states. There are more possible ways to distribute them because there are more states available what results in a higher entropy.
k-space topologies
Dispersion relation
In physics and electrical engineering, dispersion most often refers to frequency-dependent effects in wave propagation. Note, however, that there are several other uses of the word "dispersion" in the physical sciences....
that relates E to k. The dispersion relation for electrons in a solid is given by the
electronic band structure
Electronic band structure
In solid-state physics, the electronic band structure of a solid describes those ranges of energy an electron is "forbidden" or "allowed" to have. Band structure derives from the diffraction of the quantum mechanical electron waves in a periodic crystal lattice with a specific crystal system and...
.
An example of a 3-dimensional k-space is given in Fig. 1. It can be seen that the dimensionality of the system itself will confine the momentum of particles inside the system.
Density of wave vector states
The calculation for DOS starts by counting the N allowed states at a certain k that are contained within [k, k+dk] inside the volume of the system. This is done by differentiating the whole k-space volume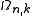in n-dimensions at an arbitrary k, with respect to k. The volume, area or length in 3, 2 or 1-dimensional k-spaces are expressed by
for a n-dimensional k-space with the topologically determined constants
for linear, disk and spherical symmetrical shaped functions in 1, 2 and 3-dimensional Euclidian k-spaces respectively.
According to this scheme the density of wave vector states N is, by differentiating
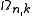with respect to k, expressed by
The 1, 2 and 3-dimensional density of wave vector states are explicitly written as
One state is large enough to contain particles having wavelength λ. The wavelength is related to k through the relationship.
In a quantum system the length of λ will depend on a characteristic spacing of the system L that is confining the particles. Finally the density of
states N is multiplied by a factor s,
where s is a constant degeneracy factor that accounts for internal degrees of freedom due to such physical phenomena as spin or polarization. If no such phenomenon is present then
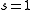. Vk is the volume in k-space containing all states whose wavevectors are smaller than a certain k serving as a parameter.Density of energy states
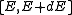To finish the calculation for DOS find the number of states per unit sample volume at an energy inside an interval . The general form of DOS of a system is given as
The scheme sketched so far only applies to continuously rising and spherically symmetric dispersion relations. In general the dispersion relation
is not spherically symmetric and in many cases it isn't continuously rising either. To express D as a function of E the inverse of the dispersion relationInverse function
In mathematics, an inverse function is a function that undoes another function: If an input x into the function ƒ produces an output y, then putting y into the inverse function g produces the output x, and vice versa. i.e., ƒ=y, and g=x...
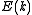has to be substituted into the expression of 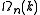as a function of k to get the expression of 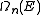as a function of the energy. If the dispersion relation is not spherically symmetric or continuously rising and can't be inverted easily then in most cases the DOS has to be calculated numerically. More detailed derivations are available.Dispersion relations
The kinetic energyKinetic energy
The kinetic energy of an object is the energy which it possesses due to its motion.It is defined as the work needed to accelerate a body of a given mass from rest to its stated velocity. Having gained this energy during its acceleration, the body maintains this kinetic energy unless its speed changes...
of a particle depends on the magnitude and direction of the wave vector
Wave vector
In physics, a wave vector is a vector which helps describe a wave. Like any vector, it has a magnitude and direction, both of which are important: Its magnitude is either the wavenumber or angular wavenumber of the wave , and its direction is ordinarily the direction of wave propagation In...
k, the properties of the particle
and the environment in which the particle is moving.
For example, the kinetic energy of an electron
Electron
The electron is a subatomic particle with a negative elementary electric charge. It has no known components or substructure; in other words, it is generally thought to be an elementary particle. An electron has a mass that is approximately 1/1836 that of the proton...
in a Fermi gas
Fermi gas
A Fermi gas is an ensemble of a large number of fermions. Fermions, named after Enrico Fermi, are particles that obey Fermi–Dirac statistics. These statistics determine the energy distribution of fermions in a Fermi gas in thermal equilibrium, and is characterized by their number density,...
is given by
where m is the electron mass. The dispersion relation is a spherically symmetric parabola and it is continuously rising so the DOS can be calculated easily.
Phonon
In physics, a phonon is a collective excitation in a periodic, elastic arrangement of atoms or molecules in condensed matter, such as solids and some liquids...
s in a string of atoms the dispersion relation of the kinetic energy in a 1-dimensional k-space, as shown in Figure 2, is given by
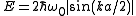
where
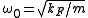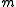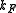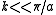is the oscillator frequency, the mass of the atoms, the inter-atomic force constant and inter-atomic spacing. For small values of the dispersion relation is rather linear: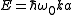When
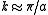the energy is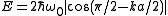With the transformation
and small 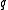this relation can be transformed to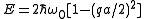Isotropic dispersion relations
The two examples mentioned here can be expressed likeThis is a kind of dispersion relation
Dispersion relation
In physics and electrical engineering, dispersion most often refers to frequency-dependent effects in wave propagation. Note, however, that there are several other uses of the word "dispersion" in the physical sciences....
because it interrelates two wave properties and it is isotropic
Isotropy
Isotropy is uniformity in all orientations; it is derived from the Greek iso and tropos . Precise definitions depend on the subject area. Exceptions, or inequalities, are frequently indicated by the prefix an, hence anisotropy. Anisotropy is also used to describe situations where properties vary...
because only the length and not the direction of the wave vector appears in the expression.
The magnitude of the wave vector is related to the energy as:
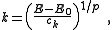
Accordingly, the volume of n-dimensional k-space containing wave vectors smaller than k is:
Substitution of the isotropic energy relation gives the volume of occupied states
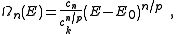
Differentiating this volume with respect to the energy gives an expression for the DOS of the isotopic dispersion relation
Parabolic dispersion
In the case of a parabolic dispersion relation (p = 2), such as applies to free electrons in a Fermi gas, theresulting density of states,
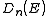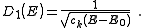
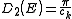
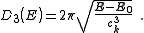
, for electrons in a n-dimensional systems isIn 1-dimensional systems the DOS diverges at the bottom of the band as
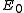drops to . In 2-dimensional systems the DOS turnsout to be independent of
. Finally for 3-dimensional systems the DOS rises as the square root of the energy.Linear dispersion
In the case of a linear relation (p = 1), such as applies to photons, or to some special kinds of electronic bands in a solid, the DOS in 1, 2 and 3 dimensional systems is related to the energy as: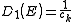Density of states and distribution functions
The density of states plays an important role in the kinetic theory of solids. The product of the density of states and the probability distribution function is the number of occupied states per unit volume at a given energy for a system in thermal equilibrium. This value is widely used to investigate various physical properties of matter. The following are examples, using two common distribution functions, of how applying a distribution function to the density of states can give rise to physical properties.Fermi-Dirac statistics
Fermi–Dirac statistics is a part of the science of physics that describes the energies of single particles in a system comprising many identical particles that obey the Pauli Exclusion Principle...
: The Fermi-Dirac probability distribution function, Fig. 4, is used to find the probability that a fermion occupies a specific quantum state in a system at thermal equilibrium. Fermions are particles which obey the Pauli Exclusion Principle
Pauli exclusion principle
The Pauli exclusion principle is the quantum mechanical principle that no two identical fermions may occupy the same quantum state simultaneously. A more rigorous statement is that the total wave function for two identical fermions is anti-symmetric with respect to exchange of the particles...
(e.g. electrons, protons, neutrons). The distribution function can be written as
is the chemical potentialChemical potential
Chemical potential, symbolized by μ, is a measure first described by the American engineer, chemist and mathematical physicist Josiah Willard Gibbs. It is the potential that a substance has to produce in order to alter a system...
(also denoted as EF and called the Fermi level
Fermi level
The Fermi level is a hypothetical level of potential energy for an electron inside a crystalline solid. Occupying such a level would give an electron a potential energy \epsilon equal to its chemical potential \mu as they both appear in the Fermi-Dirac distribution function,which...
),
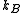is the Boltzmann constant, and 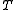is temperature. Fig. 4 illustrates how the product of the Fermi-Dirac distribution function and the three dimensional density of states for a semiconductor can give insight to physical properties such as carrier concentration and Energy band gaps.Bose-Einstein statistics: The Bose-Einstein probability distribution function is used to find the probability that a boson occupies a specific quantum state in a system at thermal equilibrium. Bosons are particles which do not obey the Pauli Exclusion Principle (e.g. phonons and photons). The distribution function can be written as
From these two distributions it is possible to calculate properties such as the internal energy
Internal energy
In thermodynamics, the internal energy is the total energy contained by a thermodynamic system. It is the energy needed to create the system, but excludes the energy to displace the system's surroundings, any energy associated with a move as a whole, or due to external force fields. Internal...
, the density of particles , specific heat capacity 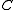, and thermal conductivityThermal conductivity
In physics, thermal conductivity, k, is the property of a material's ability to conduct heat. It appears primarily in Fourier's Law for heat conduction....
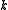. The relationships between these properties and the product of the density of states and the probability distribution, denoting the density of states by 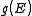instead of 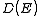, are given by
is dimensionality, is sound velocity and 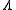is mean free pathMean free path
In physics, the mean free path is the average distance covered by a moving particle between successive impacts which modify its direction or energy or other particle properties.-Derivation:...
.
Applications
The density of states appears in many areas of physics, and helps to explain a number of quantum mechanical phenomena.Quantization
Calculating the density of states for small structures shows that the distribution of electrons changes as dimensionality is reduced. For quantum wires, the DOS for certain energies actually becomes higher than the DOS for bulk semiconductors, and for quantum dots the electrons become quantized to certain energies.Photonic crystals
The photon density of states can be manipulated by using periodic structures with length scales on the order of the wavelength of light. Some structures can completely inhibit the propagation of light of certain colors (energies), creating a photonic bandgap: the DOS is zero for those photon energies. Other structures can inhibit the propagation of light only in certain directions to create mirrors, waveguides, and cavities. Such periodic structures are known as photonic crystals.Calculation of the density of states
Interesting systems are in general complex, for instance compounds, biomolecules, polymers, etc. Because of the complexity of these systems the analytical calculation of the density of states is in most of the cases impossible.Computer simulations offer a set of algorithms to evaluate the density of states with a high accuracy. One of these
algorithms is called the Wang and Landau algorithm
Wang and Landau algorithm
The Wang and Landau algorithm proposed by Fugao Wang and David P. Landau is an extension of Metropolis Monte Carlo sampling. It is designed to calculate the density of states of a computer-simulated system, such as an Ising model of spin glasses, or model atoms in a molecular force field...
.
Within the Wang and Landau scheme any previous knowledge of the density of states is required. One proceed as follows:
the cost function (for example the energy) of the system is discretized. Each time the bin i is reached one update
a histogram for the density of, states
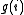,by,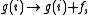where f is called modification factor. As soon as each bin in the histogram is visited a certain number of times
(10-15), the modification factor is reduced by some criterion, for instance,
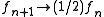
where n denotes the n-th update step. The simulation finishes when the modification factor is less than a certain threshold, for instance
.The Wang and Landau algorithm has some advantages over other common algorithms such as multicanonical simulations and
Parallel tempering
Parallel tempering
Parallel tempering, also known as replica exchange MCMC sampling, is a simulation method aimed at improving the dynamic properties of Monte Carlo method simulations of physical systems, and of Markov chain Monte Carlo sampling methods more generally...
, for instance, the density of states is obtained as the main product of the simulation.
Additionally, Wang and Landau simulations are completely independent of the temperature. This feature allows to compute the density of states of systems with very rough energy landscape such as proteins.
See also
- Effective mass (solid-state physics)
- Band structure
- k·p perturbation theoryK·p perturbation theoryIn solid-state physics, k·p perturbation theory is an approximation scheme for calculating the band structure and optical properties of crystalline solids. It is pronounced "k dot p", and is also called the "k·p method"...
- SemiconductorSemiconductorA semiconductor is a material with electrical conductivity due to electron flow intermediate in magnitude between that of a conductor and an insulator. This means a conductivity roughly in the range of 103 to 10−8 siemens per centimeter...
- Electrical conduction
- Valence bandValence bandIn solids, the valence band is the highest range of electron energies in which electrons are normally present at absolute zero temperature....
- Kronig-Penney model
- Tight-binding model
- Muffin-tin approximationMuffin-tin approximationThe muffin-tin approximation is a shape approximation of the potential field in an atomistic environment. It is most commonly employed in quantum mechanical simulations of electronic band structure in solids. The approximation was proposed by John C. Slater. Many modern electronic structure methods...
Further reading
- Chen, Gang. Nanoscale Energy Transport and Conversion. New York: Oxford, 2005
- Streetman, Ben G. and Sanjay Banerjee. Solid State Electronic Devices. Upper Saddle River, NJ: Prentice Hall, 2000.
- Muller, Richard S. and Theodore I. Kamins. Device Electronics for Integrated Circuits. New York: John Wiley and Sons, 2003.
- Kittel, Charles and Herbert Kroemer. Thermal Physics. New York: W.H. Freeman and Company, 1980
- Sze, Simon M. Physics of Semiconductor Devices. New York: John Wiley and Sons, 1981