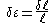Deformation (mechanics)
Encyclopedia
Deformation in continuum mechanics
is the transformation of a body from a reference configuration to a current configuration. A configuration is a set containing the positions of all particles of the body. Contrary to the common definition of deformation, which implies distortion
or change in shape, the continuum mechanics definition includes rigid body motions where shape changes do not take place ( footnote 4, p. 48).
The cause of a deformation is not pertinent to the definition of the term. However, it is usually assumed that a deformation is caused by external loads, body forces (such as gravity or electromagnetic forces), or temperature changes within the body.
Strain is a description of deformation in terms of relative displacement of particles in the body.
Different equivalent choices may be made for the expression of a strain field depending on whether it is defined in the initial or in the final placement and on whether the metric tensor or its dual is considered.
In a continuous body, a deformation field results from a stress
field induced by applied force
s or is due to changes in the temperature field inside the body. The relation between stresses and induced strains is expressed by constitutive equations, e.g., Hooke's law
for linear elastic
materials. Deformations which are recovered after the stress field has been removed are called elastic deformations. In this case, the continuum completely recovers its original configuration. On the other hand, irreversible deformations remain even after stresses have been removed. One type of irreversible deformation is plastic deformation, which occurs in material bodies after stresses have attained a certain threshold value known as the elastic limit or yield stress
, and are the result of slip
, or dislocation
mechanisms at the atomic level. Another type of irreversible deformation is viscous deformation, which is the irreversible part of viscoelastic deformation.
In the case of elastic deformations, the response function linking strain to the deforming stress is the compliance tensor of the material.
A general deformation of a body can be expressed in the form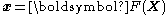
where 
is the reference position of material points in the body. Such a measure does not distinguish between rigid body motions (translations and rotations) and changes in shape (and size) of the body. A deformation has units of length.
We could, for example, define strain to be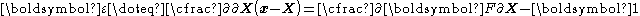
.
Hence strains are dimensionless and are usually expressed as a decimal fraction
, a percentage
or in parts-per notation
. Strains measure how much a given deformation differs locally from a rigid-body deformation.
A strain is in general a tensor
quantity. Physical insight into strains can be gained by observing that a given strain can be decomposed into normal and shear components. The amount of stretch or compression along a material line elements or fibers is the normal strain, and the amount of distortion associated with the sliding of plane layers over each other is the shear strain, within a deforming body. This could be applied by elongation, shortening, or volume changes, or angular distortion.
The state of strain at a material point
of a continuum body is defined as the totality of all the changes in length of material lines or fibers, the normal strain, which pass through that point and also the totality of all the changes in the angle between pairs of lines initially perpendicular to each other, the shear strain, radiating from this point. However, it is sufficient to know the normal and shear components of strain on a set of three mutually perpendicular directions.
If there is an increase in length of the material line, the normal strain is called tensile strain, otherwise, if there is reduction or compression in the length of the material line, it is called compressive strain.
In each of these theories the strain is then defined differently. The engineering strain is the most common definition applied to materials used in mechanical and structural engineering, which are subjected to very small deformations. On the other hand, for some materials, e.g. elastomers and polymers, subjected to large deformations, the engineering definition of strain is not applicable, e.g. typical engineering strains greater than 1%, thus other more complex definitions of strain are required, such as stretch, logarithmic strain, Green strain, and Almansi strain.
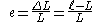
where
is the engineering normal strain, 
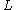is the original length of the fiber and 
is the final length of the fiber.
The true shear strain is defined as the change in the angle (in radians) between two material line elements initially perpendicular to each other in the undeformed or initial configuration. The engineering shear strain is defined as the tangent of that angle, and is equal to the length of deformation at its maximum divided by the perpendicular length in the plane of force application which sometimes makes it easier to calculate.
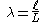
The extension ratio is approximately related to the engineering strain by
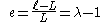
This equation implies that the normal strain is zero, so that there is no deformation when the stretch is equal to unity.
The stretch ratio is used in the analysis of materials that exhibit large deformations, such as elastomers, which can sustain stretch ratios of 3 or 4 before they fail. On the other hand, traditional engineering materials, such as concrete or steel, fail at much lower stretch ratios.
the logarithmic strain is obtained by integrating this incremental strain:
where e is the engineering strain. The logarithmic strain provides the correct measure of the final strain when deformation takes place in a series of increments, taking into account the influence of the strain path.
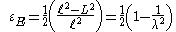
As with stresses, strains may also be classified as 'normal strain' and 'shear strain' (i.e. acting perpendicular to or along the face of an element respectively). For an isotropic material that obeys Hooke's law
, a normal stress will cause a normal strain. Normal strains produce dilations.
Consider a two-dimensional infinitesimal rectangular material element with dimensions
, which after deformation, takes the form of a rhombus. From the geometry of the adjacent figure we have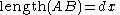
and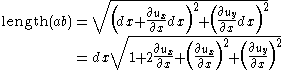
For very small displacement gradients the squares of the derivatives are negligible and we have
The normal strain in the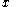
-direction of the rectangular element is defined by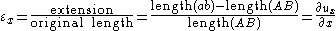
Similarly, the normal strain in the
-direction, and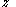 
-direction, becomes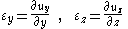
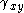) is the change in angle between lines 
and 
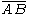. Therefore,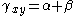
From the geometry of the figure, we have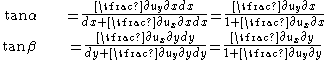
For small displacement gradients we have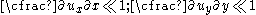
For small rotations, i.e.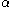
and 
are 
we have
.
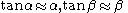Therefore,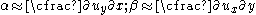
thus
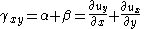
By interchanging
and 
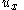and 
and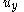 
, it can be shown that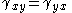 
Similarly, for the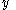
-
and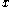 
-
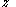planes, we have
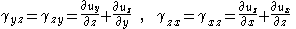
The tensorial shear strain components of the infinitesimal strain tensor can then be expressed using the engineering strain definition,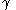
, as
A basic geometric result, due to Fréchet, von Neumann
and Jordan
, states that, if the lengths of the tangent vectors fulfill the axioms of a norm
and the parallelogram law
, then the length of a vector is the square root of the value of the quadratic form associated, by the polarization formula, with a positive definite bilinear map called the metric tensor
.
displacement occurred.
It is convenient to identify a reference configuration or initial geometric state of the continuum body which all subsequent configurations are referenced from. The reference configuration need not to be one the body actually will ever occupy. Often, the configuration at is considered the reference configuration, κ0(B). The configuration at the current time t is the current configuration.
For deformation analysis, the reference configuration is identified as undeformed configuration, and the current configuration as deformed configuration. Additionally, time is not considered when analyzing deformation, thus the sequence of configurations between the undeformed and deformed configurations are of no interest.
The components Xi of the position vector X of a particle in the reference configuration, taken with respect to the reference coordinate system, are called the material or reference coordinates. On the other hand, the components xi of the position vector x of a particle in the deformed configuration, taken with respect to the spatial coordinate system of reference, are called the spatial coordinates
There are two methods for analysing the deformation of a continuum. One description is made in terms of the material or referential coordinates, called material description or Lagrangian description
. A second description is of deformation is made in terms of the spatial coordinates it is called the spatial description or Eulerian description
.
There is continuity during deformation of a continuum body in the sense that:
. Such a transformation is composed of a linear transformation
(such as rotation, shear, extension and compression) and a rigid body translation. Affine deformations are also called homogeneous deformations.
Therefore an affine deformation has the form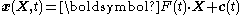
where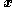
is the position of a point in the deformed configuration, 
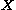is the position in a reference configuration, 
is a time-like parameter, 
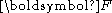is the linear transformer and 
is the translation. In matrix form, where the components are with respect to an orthonormal basis,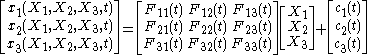
The above deformation becomes non-affine or inhomogeneous if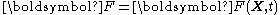
or 
.
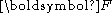is proper orthogonal
in order to allow rotations but no reflection
s.
A rigid body motion can be described by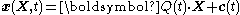
where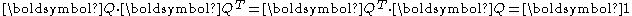
In matrix form,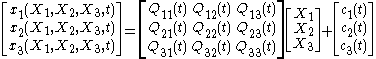
. The displacement of a body has two components: a rigid-body displacement and a deformation. A rigid-body displacement consist of a simultaneous translation and rotation of the body without changing its shape or size. Deformation implies the change in shape and/or size of the body from an initial or undeformed configuration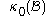
to a current or deformed configuration 
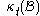(Figure 1).
If after a displacement of the continuum there is a relative displacement between particles, a deformation has occurred. On the other hand, if after displacement of the continuum the relative displacement between particles in the current configuration is zero, then there is no deformation and a rigid-body displacement is said to have occurred.
The vector joining the positions of a particle P in the undeformed configuration and deformed configuration is called the displacement vector
in the Lagrangian description, or in the Eulerian description.
A displacement field is a vector field of all displacement vectors for all particles in the body, which relates the deformed configuration with the undeformed configuration. It is convenient to do the analysis of deformation or motion of a continuum body in terms of the displacement field, In general, the displacement field is expressed in terms of the material coordinates as
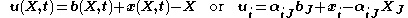
or in terms of the spatial coordinates as
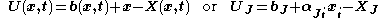
where αJi are the direction cosines between the material and spatial coordinate systems with unit vectors EJ and ei, respectively. Thus
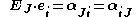
and the relationship between ui and UJ is then given by
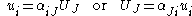
Knowing that
then
It is common to superimpose the coordinate systems for the undeformed and deformed configurations, which results in , and the direction cosines become Kronecker deltas:
Thus, we have
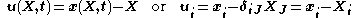
or in terms of the spatial coordinates as
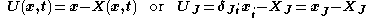
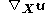. Thus we have:
where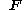
is the deformation gradient tensor.
Similarly, the partial differentiation of the displacement vector with respect to the spatial coordinates yields the spatial displacement gradient tensor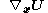
. Thus we have,
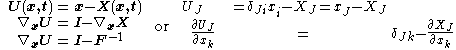
Plane deformations are also of interest, particularly in the experimental context.
, the deformation gradient has the form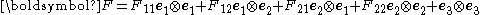
In matrix form,
From the polar decomposition theorem, the deformation gradient, up to a change of coordinates, can be decomposed into a stretch and a rotation. Since all the deformation is in a plane, we can write
where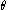
is the angle of rotation and 
,
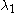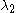are the principal stretches.
and we
have
Alternatively,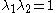
If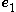
is the fixed reference orientation in which line elements do not deform during the deformation then 
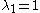and 
.
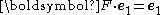Therefore,
Since the deformation is isochoric,
Define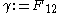
. Then, the deformation gradient in simple shear can be expressed as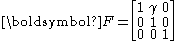
Now,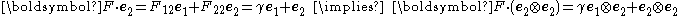
Since
we can also write the deformation gradient as
Continuum mechanics
Continuum mechanics is a branch of mechanics that deals with the analysis of the kinematics and the mechanical behavior of materials modelled as a continuous mass rather than as discrete particles...
is the transformation of a body from a reference configuration to a current configuration. A configuration is a set containing the positions of all particles of the body. Contrary to the common definition of deformation, which implies distortion
Distortion
A distortion is the alteration of the original shape of an object, image, sound, waveform or other form of information or representation. Distortion is usually unwanted, and often many methods are employed to minimize it in practice...
or change in shape, the continuum mechanics definition includes rigid body motions where shape changes do not take place ( footnote 4, p. 48).
The cause of a deformation is not pertinent to the definition of the term. However, it is usually assumed that a deformation is caused by external loads, body forces (such as gravity or electromagnetic forces), or temperature changes within the body.
Strain is a description of deformation in terms of relative displacement of particles in the body.
Different equivalent choices may be made for the expression of a strain field depending on whether it is defined in the initial or in the final placement and on whether the metric tensor or its dual is considered.
In a continuous body, a deformation field results from a stress
Stress (physics)
In continuum mechanics, stress is a measure of the internal forces acting within a deformable body. Quantitatively, it is a measure of the average force per unit area of a surface within the body on which internal forces act. These internal forces are a reaction to external forces applied on the body...
field induced by applied force
Force
In physics, a force is any influence that causes an object to undergo a change in speed, a change in direction, or a change in shape. In other words, a force is that which can cause an object with mass to change its velocity , i.e., to accelerate, or which can cause a flexible object to deform...
s or is due to changes in the temperature field inside the body. The relation between stresses and induced strains is expressed by constitutive equations, e.g., Hooke's law
Hooke's law
In mechanics, and physics, Hooke's law of elasticity is an approximation that states that the extension of a spring is in direct proportion with the load applied to it. Many materials obey this law as long as the load does not exceed the material's elastic limit. Materials for which Hooke's law...
for linear elastic
Linear elasticity
Linear elasticity is the mathematical study of how solid objects deform and become internally stressed due to prescribed loading conditions. Linear elasticity models materials as continua. Linear elasticity is a simplification of the more general nonlinear theory of elasticity and is a branch of...
materials. Deformations which are recovered after the stress field has been removed are called elastic deformations. In this case, the continuum completely recovers its original configuration. On the other hand, irreversible deformations remain even after stresses have been removed. One type of irreversible deformation is plastic deformation, which occurs in material bodies after stresses have attained a certain threshold value known as the elastic limit or yield stress
Yield (engineering)
The yield strength or yield point of a material is defined in engineering and materials science as the stress at which a material begins to deform plastically. Prior to the yield point the material will deform elastically and will return to its original shape when the applied stress is removed...
, and are the result of slip
Slip (materials science)
In materials science, Slip is the process by which plastic deformation is produced by a dislocation motion. By an external force, parts of the crystal lattice glide along each other, resulting in a changed geometry of the material. Depending on the type of lattice, different slip systems are...
, or dislocation
Dislocation
In materials science, a dislocation is a crystallographic defect, or irregularity, within a crystal structure. The presence of dislocations strongly influences many of the properties of materials...
mechanisms at the atomic level. Another type of irreversible deformation is viscous deformation, which is the irreversible part of viscoelastic deformation.
In the case of elastic deformations, the response function linking strain to the deforming stress is the compliance tensor of the material.
Strain
A strain is a normalized measure of deformation representing the displacement between particles in the body relative to a reference length.A general deformation of a body can be expressed in the form
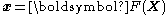where is the reference position of material points in the body. Such a measure does not distinguish between rigid body motions (translations and rotations) and changes in shape (and size) of the body. A deformation has units of length.We could, for example, define strain to be
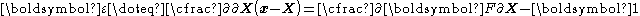.Hence strains are dimensionless and are usually expressed as a decimal fraction
Decimal
The decimal numeral system has ten as its base. It is the numerical base most widely used by modern civilizations....
, a percentage
Percentage
In mathematics, a percentage is a way of expressing a number as a fraction of 100 . It is often denoted using the percent sign, “%”, or the abbreviation “pct”. For example, 45% is equal to 45/100, or 0.45.Percentages are used to express how large/small one quantity is, relative to another quantity...
or in parts-per notation
Parts-per notation
In science and engineering, the parts-per notation is a set of pseudo units to describe small values of miscellaneous dimensionless quantities, e.g. mole fraction or mass fraction. Since these fractions are quantity-per-quantity measures, they are pure numbers with no associated units of measurement...
. Strains measure how much a given deformation differs locally from a rigid-body deformation.
A strain is in general a tensor
Tensor
Tensors are geometric objects that describe linear relations between vectors, scalars, and other tensors. Elementary examples include the dot product, the cross product, and linear maps. Vectors and scalars themselves are also tensors. A tensor can be represented as a multi-dimensional array of...
quantity. Physical insight into strains can be gained by observing that a given strain can be decomposed into normal and shear components. The amount of stretch or compression along a material line elements or fibers is the normal strain, and the amount of distortion associated with the sliding of plane layers over each other is the shear strain, within a deforming body. This could be applied by elongation, shortening, or volume changes, or angular distortion.
The state of strain at a material point
Continuum mechanics
Continuum mechanics is a branch of mechanics that deals with the analysis of the kinematics and the mechanical behavior of materials modelled as a continuous mass rather than as discrete particles...
of a continuum body is defined as the totality of all the changes in length of material lines or fibers, the normal strain, which pass through that point and also the totality of all the changes in the angle between pairs of lines initially perpendicular to each other, the shear strain, radiating from this point. However, it is sufficient to know the normal and shear components of strain on a set of three mutually perpendicular directions.
If there is an increase in length of the material line, the normal strain is called tensile strain, otherwise, if there is reduction or compression in the length of the material line, it is called compressive strain.
Strain measures
Depending on the amount of strain, or local deformation, the analysis of deformation is subdivided into three deformation theories:- Finite strain theory, also called large strain theory, large deformation theory, deals with deformations in which both rotations and strains are arbitrarily large. In this case, the undeformed and deformed configurations of the continuumContinuum mechanicsContinuum mechanics is a branch of mechanics that deals with the analysis of the kinematics and the mechanical behavior of materials modelled as a continuous mass rather than as discrete particles...
are significantly different and a clear distinction has to be made between them. This is commonly the case with elastomerElastomerAn elastomer is a polymer with the property of viscoelasticity , generally having notably low Young's modulus and high yield strain compared with other materials. The term, which is derived from elastic polymer, is often used interchangeably with the term rubber, although the latter is preferred...
s, plastically-deformingPlasticity (physics)In physics and materials science, plasticity describes the deformation of a material undergoing non-reversible changes of shape in response to applied forces. For example, a solid piece of metal being bent or pounded into a new shape displays plasticity as permanent changes occur within the...
materials and other fluidFluidIn physics, a fluid is a substance that continually deforms under an applied shear stress. Fluids are a subset of the phases of matter and include liquids, gases, plasmas and, to some extent, plastic solids....
s and biological soft tissueSoft tissueIn anatomy, the term soft tissue refers to tissues that connect, support, or surround other structures and organs of the body, not being bone. Soft tissue includes tendons, ligaments, fascia, skin, fibrous tissues, fat, and synovial membranes , and muscles, nerves and blood vessels .It is sometimes...
. - Infinitesimal strain theory, also called small strain theory, small deformation theory, small displacement theory, or small displacement-gradient theory where strains and rotations are both small. In this case, the undeformed and deformed configurations of the body can be assumed identical. The infinitesimal strain theory is used in the analysis of deformations of materials exhibiting elastic behavior, such as materials found in mechanical and civil engineering applications, e.g. concrete and steel.
- Large-displacement or large-rotation theory, which assumes small strains but large rotations and displacements.
In each of these theories the strain is then defined differently. The engineering strain is the most common definition applied to materials used in mechanical and structural engineering, which are subjected to very small deformations. On the other hand, for some materials, e.g. elastomers and polymers, subjected to large deformations, the engineering definition of strain is not applicable, e.g. typical engineering strains greater than 1%, thus other more complex definitions of strain are required, such as stretch, logarithmic strain, Green strain, and Almansi strain.
Engineering strain
The Cauchy strain or engineering strain is expressed as the ratio of total deformation to the initial dimension of the material body in which the forces are being applied. The engineering normal strain or engineering extensional strain or nominal strain e of a material line element or fiber axially loaded is expressed as the change in length ΔL per unit of the original length L of the line element or fibers. The normal strain is positive if the material fibers are stretched or negative if they are compressed. Thus, we have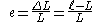where
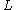is the engineering normal strain, is the original length of the fiber and is the final length of the fiber.The true shear strain is defined as the change in the angle (in radians) between two material line elements initially perpendicular to each other in the undeformed or initial configuration. The engineering shear strain is defined as the tangent of that angle, and is equal to the length of deformation at its maximum divided by the perpendicular length in the plane of force application which sometimes makes it easier to calculate.
Stretch ratio
The stretch ratio or extension ratio is a measure of the extensional or normal strain of a differential line element, which can be defined at either the undeformed configuration or the deformed configuration. It is defined as the ratio between the final length ℓ and the initial length L of the material line.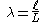The extension ratio is approximately related to the engineering strain by
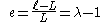
This equation implies that the normal strain is zero, so that there is no deformation when the stretch is equal to unity.
The stretch ratio is used in the analysis of materials that exhibit large deformations, such as elastomers, which can sustain stretch ratios of 3 or 4 before they fail. On the other hand, traditional engineering materials, such as concrete or steel, fail at much lower stretch ratios.
True strain
The logarithmic strain ε, also called natural strain, true strain or Hencky strain. Considering an incremental strain (Ludwik)
the logarithmic strain is obtained by integrating this incremental strain:
where e is the engineering strain. The logarithmic strain provides the correct measure of the final strain when deformation takes place in a series of increments, taking into account the influence of the strain path.
Green strain
The Green strain is defined as:Almansi strain
The Euler-Almansi strain is defined as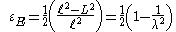Normal strain
Hooke's law
In mechanics, and physics, Hooke's law of elasticity is an approximation that states that the extension of a spring is in direct proportion with the load applied to it. Many materials obey this law as long as the load does not exceed the material's elastic limit. Materials for which Hooke's law...
, a normal stress will cause a normal strain. Normal strains produce dilations.
Consider a two-dimensional infinitesimal rectangular material element with dimensions
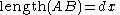
, which after deformation, takes the form of a rhombus. From the geometry of the adjacent figure we haveand
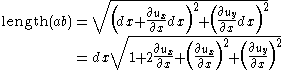
For very small displacement gradients the squares of the derivatives are negligible and we have
The normal strain in the
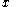-direction of the rectangular element is defined by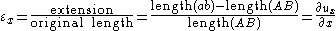Similarly, the normal strain in the
-direction, and 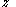-direction, becomes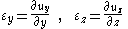Shear strain
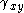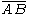The engineering shear strain is defined as () is the change in angle between lines and . Therefore,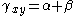From the geometry of the figure, we have
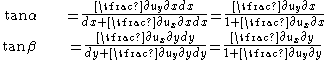
For small displacement gradients we have
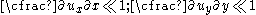
For small rotations, i.e.
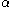and are we have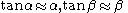.Therefore,
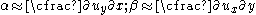
thus
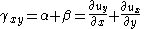
By interchanging
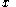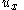and and and 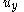, it can be shown that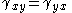 Similarly, for the
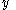- and 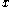- 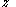planes, we have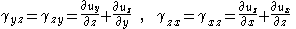The tensorial shear strain components of the infinitesimal strain tensor can then be expressed using the engineering strain definition,
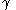, asMetric tensor
A strain field associated with a displacement is defined, at any point, by the change in length of the tangent vectors representing the speeds of arbitrarily parametrized curves passing through that point.A basic geometric result, due to Fréchet, von Neumann
John von Neumann
John von Neumann was a Hungarian-American mathematician and polymath who made major contributions to a vast number of fields, including set theory, functional analysis, quantum mechanics, ergodic theory, geometry, fluid dynamics, economics and game theory, computer science, numerical analysis,...
and Jordan
Pascual Jordan
-Further reading:...
, states that, if the lengths of the tangent vectors fulfill the axioms of a norm
Norm
-In academia:A designated standard of average performance of people of a given age, background, etc.*Norm , a set of statements used to regulate artificial intelligence software...
and the parallelogram law
Parallelogram law
In mathematics, the simplest form of the parallelogram law belongs to elementary geometry. It states that the sum of the squares of the lengths of the four sides of a parallelogram equals the sum of the squares of the lengths of the two diagonals...
, then the length of a vector is the square root of the value of the quadratic form associated, by the polarization formula, with a positive definite bilinear map called the metric tensor
Metric tensor
In the mathematical field of differential geometry, a metric tensor is a type of function defined on a manifold which takes as input a pair of tangent vectors v and w and produces a real number g in a way that generalizes many of the familiar properties of the dot product of vectors in Euclidean...
.
Description of deformation
Deformation is the change in the metric properties of a continuous body, meaning that a curve drawn in the initial body placement changes its length when displaced to a curve in the final placement. If all the curves do not change length, it is said that a rigid bodyRigid body
In physics, a rigid body is an idealization of a solid body of finite size in which deformation is neglected. In other words, the distance between any two given points of a rigid body remains constant in time regardless of external forces exerted on it...
displacement occurred.
It is convenient to identify a reference configuration or initial geometric state of the continuum body which all subsequent configurations are referenced from. The reference configuration need not to be one the body actually will ever occupy. Often, the configuration at is considered the reference configuration, κ0(B). The configuration at the current time t is the current configuration.
For deformation analysis, the reference configuration is identified as undeformed configuration, and the current configuration as deformed configuration. Additionally, time is not considered when analyzing deformation, thus the sequence of configurations between the undeformed and deformed configurations are of no interest.
The components Xi of the position vector X of a particle in the reference configuration, taken with respect to the reference coordinate system, are called the material or reference coordinates. On the other hand, the components xi of the position vector x of a particle in the deformed configuration, taken with respect to the spatial coordinate system of reference, are called the spatial coordinates
There are two methods for analysing the deformation of a continuum. One description is made in terms of the material or referential coordinates, called material description or Lagrangian description
Continuum mechanics
Continuum mechanics is a branch of mechanics that deals with the analysis of the kinematics and the mechanical behavior of materials modelled as a continuous mass rather than as discrete particles...
. A second description is of deformation is made in terms of the spatial coordinates it is called the spatial description or Eulerian description
Continuum mechanics
Continuum mechanics is a branch of mechanics that deals with the analysis of the kinematics and the mechanical behavior of materials modelled as a continuous mass rather than as discrete particles...
.
There is continuity during deformation of a continuum body in the sense that:
- The material points forming a closed curve at any instant will always form a closed curve at any subsequent time.
- The material points forming a closed surface at any instant will always form a closed surface at any subsequent time and the matter within the closed surface will always remain within.
Affine deformation
A deformation is called an affine deformation, if it can be described by an affine transformationAffine transformation
In geometry, an affine transformation or affine map or an affinity is a transformation which preserves straight lines. It is the most general class of transformations with this property...
. Such a transformation is composed of a linear transformation
Linear transformation
In mathematics, a linear map, linear mapping, linear transformation, or linear operator is a function between two vector spaces that preserves the operations of vector addition and scalar multiplication. As a result, it always maps straight lines to straight lines or 0...
(such as rotation, shear, extension and compression) and a rigid body translation. Affine deformations are also called homogeneous deformations.
Therefore an affine deformation has the form
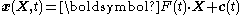
where
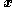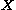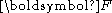is the position of a point in the deformed configuration, is the position in a reference configuration, is a time-like parameter, is the linear transformer and is the translation. In matrix form, where the components are with respect to an orthonormal basis,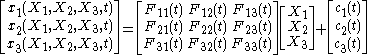The above deformation becomes non-affine or inhomogeneous if
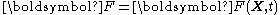or .Rigid body motion
A rigid body motion is a special affine deformation that does not involve any shear, extension or compression. The transformation matrix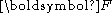 is proper orthogonalOrthogonal matrix
In linear algebra, an orthogonal matrix , is a square matrix with real entries whose columns and rows are orthogonal unit vectors ....
in order to allow rotations but no reflection
Reflection (mathematics)
In mathematics, a reflection is a mapping from a Euclidean space to itself that is an isometry with a hyperplane as set of fixed points; this set is called the axis or plane of reflection. The image of a figure by a reflection is its mirror image in the axis or plane of reflection...
s.
A rigid body motion can be described by
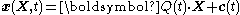
where
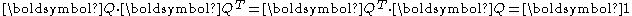
In matrix form,
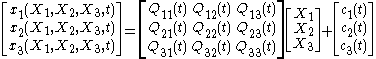
Displacement
A change in the configuration of a continuum body results in a displacementDisplacement field (mechanics)
A displacement field is an assignment of displacement vectors for all points in a region or body that is displaced from one state to another. A displacement vector specifies the position of a point or a particle in reference to an origin or to a previous position...
. The displacement of a body has two components: a rigid-body displacement and a deformation. A rigid-body displacement consist of a simultaneous translation and rotation of the body without changing its shape or size. Deformation implies the change in shape and/or size of the body from an initial or undeformed configuration
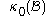to a current or deformed configuration 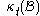(Figure 1).If after a displacement of the continuum there is a relative displacement between particles, a deformation has occurred. On the other hand, if after displacement of the continuum the relative displacement between particles in the current configuration is zero, then there is no deformation and a rigid-body displacement is said to have occurred.
The vector joining the positions of a particle P in the undeformed configuration and deformed configuration is called the displacement vector
Displacement (vector)
A displacement is the shortest distance from the initial to the final position of a point P. Thus, it is the length of an imaginary straight path, typically distinct from the path actually travelled by P...
in the Lagrangian description, or in the Eulerian description.
A displacement field is a vector field of all displacement vectors for all particles in the body, which relates the deformed configuration with the undeformed configuration. It is convenient to do the analysis of deformation or motion of a continuum body in terms of the displacement field, In general, the displacement field is expressed in terms of the material coordinates as
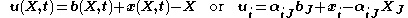
or in terms of the spatial coordinates as
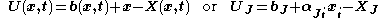
where αJi are the direction cosines between the material and spatial coordinate systems with unit vectors EJ and ei, respectively. Thus
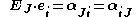
and the relationship between ui and UJ is then given by
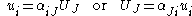
Knowing that
then
It is common to superimpose the coordinate systems for the undeformed and deformed configurations, which results in , and the direction cosines become Kronecker deltas:
Thus, we have
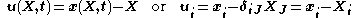
or in terms of the spatial coordinates as
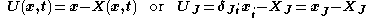
Displacement gradient tensor
The partial differentiation of the displacement vector with respect to the material coordinates yields the material displacement gradient tensor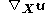. Thus we have:where
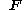is the deformation gradient tensor.Similarly, the partial differentiation of the displacement vector with respect to the spatial coordinates yields the spatial displacement gradient tensor
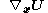. Thus we have,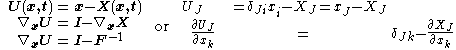Examples of deformations
Homogeneous (or affine) deformations are useful in elucidating the behavior of materials. Some homogeneous deformations of interest are- uniform extension
- pure dilation
- simple shear
- pure shear
Plane deformations are also of interest, particularly in the experimental context.
Plane deformation
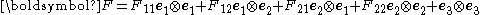
A plane deformation, also called plane strain, is one where the deformation is restricted to one of the planes in the reference configuration. If the deformation is restricted to the plane described by the basis vectors, the deformation gradient has the formIn matrix form,
From the polar decomposition theorem, the deformation gradient, up to a change of coordinates, can be decomposed into a stretch and a rotation. Since all the deformation is in a plane, we can write
where
is the angle of rotation and 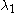, 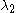are the principal stretches.Isochoric plane deformation
If the deformation is isochoric (volume preserving) then and wehave
Alternatively,
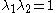
Simple shear
A simple shear deformation is defined as an isochoric plane deformation in which there are a set of line elements with a given reference orientation that do not change length and orientation during the deformation.If
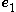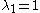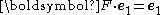is the fixed reference orientation in which line elements do not deform during the deformation then and .Therefore,
Since the deformation is isochoric,
Define
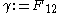. Then, the deformation gradient in simple shear can be expressed as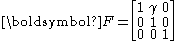Now,
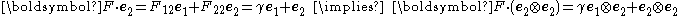
Since
we can also write the deformation gradient asSee also
- Deformation (engineering)
- Finite strain theory
- Infinitesimal strain theory
- Moiré patternMoiré patternIn physics, a moiré pattern is an interference pattern created, for example, when two grids are overlaid at an angle, or when they have slightly different mesh sizes.- Etymology :...
- Shear modulus
- Shear stressShear stressA shear stress, denoted \tau\, , is defined as the component of stress coplanar with a material cross section. Shear stress arises from the force vector component parallel to the cross section...
- Shear strengthShear strengthShear strength in engineering is a term used to describe the strength of a material or component against the type of yield or structural failure where the material or component fails in shear. A shear load is a force that tends to produce a sliding failure on a material along a plane that is...
- Stress (mechanics)
- Stress measuresStress measuresThe most commonly used measure of stress is the Cauchy stress. However, several other measures of stress can be defined. Some such stress measures that are widely used in continuum mechanics, particularly in the computational context, are:...