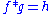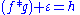Deconvolution
Encyclopedia
In mathematics
, deconvolution is an algorithm-based
process used to reverse the effects of convolution
on recorded data. The concept of deconvolution is widely used in the techniques of signal processing
and image processing
. Because these techniques are in turn widely used in many scientific
and engineering
disciplines, deconvolution finds many applications.
In general, the object of deconvolution is to find the solution of a convolution equation of the form:
Usually, h is some recorded signal, and ƒ is some signal that we wish to recover, but has been convolved with some other signal g before we recorded it. The function g might represent the transfer function
of an instrument or a driving force that was applied to a physical system. If we know g, or at least know the form of g, then we can perform deterministic deconvolution. However, if we do not know g in advance, then we need to estimate it. This is most often done using methods of statistical
estimation
.
In physical measurements, the situation is usually closer to
In this case ε is noise that has entered our recorded signal. If we assume that a noisy signal or image is noiseless when we try to make a statistical estimate of g, our estimate will be incorrect. In turn, our estimate of ƒ will also be incorrect. The lower the signal-to-noise ratio
, the worse our estimate of the deconvolved signal will be. That is the reason why usually inverse filter
ing the signal is not a good solution. However, if we have at least some knowledge of the type of noise in the data (for example, white noise
), we may be able to improve the estimate of ƒ through techniques such as Wiener deconvolution
.
The foundations for deconvolution and time-series analysis were largely laid by Norbert Wiener
of the Massachusetts Institute of Technology
in his book Extrapolation, Interpolation, and Smoothing of Stationary Time Series (1949). The book was based on work Wiener had done during World War II
but that had been classified at the time. Some of the early attempts to apply these theories were in the fields of weather forecasting
and economics
.
. In 1950, Enders Robinson was a graduate student at MIT. He worked with others at MIT, such as Norbert Wiener
, Norman Levinson
, and economist Paul Samuelson
, to develop the "convolutional model" of a reflection seismogram. This model assumes that the recorded seismogram
s(t) is the convolution of an Earth-reflectivity function e(t) and a seismic wavelet w(t) from a point source
, where t represents recording time. Thus, our convolution equation is
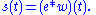
The seismologist is interested in e, which contains information about the Earth's structure. By the convolution theorem
, this equation may be Fourier transform
ed to
in the frequency domain
. By assuming that the reflectivity is white, we can assume that the power spectrum
of the reflectivity is constant, and that the power spectrum of the seismogram is the spectrum of the wavelet multiplied by that constant. Thus,
If we assume that the wavelet is minimum phase
, we can recover it by calculating the minimum phase equivalent of the power spectrum we just found. The reflectivity may be recovered by designing and applying a Wiener filter
that shapes the estimated wavelet to a Dirac delta function
(i.e., a spike). The result may be seen as a series of scaled, shifted delta functions (although this is not mathematically rigorous):
where N is the number of reflection events, τ i τ i are the reflection times of each event, and r i are the reflection coefficient
s.
In practice, since we are dealing with noisy, finite bandwidth
, finite length, discretely sampled datasets, the above procedure only yields an approximation of the filter required to deconvolve the data. However, by formulating the problem as the solution of a Toeplitz matrix
and using Levinson recursion
, we can relatively quickly estimate a filter with the smallest mean squared error
possible. We can also do deconvolution directly in the frequency domain and get similar results. The technique is closely related to linear prediction
.
, electron microscope
, telescope
, or other imaging instrument, thus creating clearer images. It is usually done in the digital domain by a software algorithm
, as part of a suite of microscope image processing
techniques. Deconvolution is also practical to sharpen images that suffer from fast motion or jiggles during capturing. Early Hubble Space Telescope
images were distorted by a flawed mirror and could be sharpened by deconvolution.
The usual method is to assume that the optical path through the instrument is optically perfect, convolved with a point spread function
(PSF), that is, a mathematical function that describes the distortion in terms of the pathway a theoretical point source
of light (or other waves) takes through the instrument. Usually, such a point source contributes a small area of fuzziness to the final image. If this function can be determined, it is then a matter of computing its inverse
or complementary function, and convolving the acquired image with that. The result is the original, undistorted image.
In practice, finding the true PSF is impossible, and usually an approximation of it is used, theoretically calculated or based on some experimental estimation by using known probes. Real optics may also have different PSFs at different focal and spatial locations, and the PSF may be non-linear. The accuracy of the approximation of the PSF will dictate the final result. Different algorithms can be employed to give better results, at the price of being more computationally intensive. Since the original convolution discards data, some algorithms use additional data acquired at nearby focal points to make up some of the lost information. Regularization
in iterative algorithms (as in expectation-maximization algorithm
s) can be applied to avoid unrealistic solutions.
When the PSF is unknown, it may be possible to deduce it by systematically trying different possible PSFs and assessing whether the image has improved. This procedure is called blind deconvolution
. Blind deconvolution is a well-established image restoration technique in astronomy
, where the point nature of the objects photographed exposes the PSF thus making it more feasible. It is also used in fluorescence microscopy for image restoration, and in fluorescence spectral imaging
for spectral separation of multiple unknown fluorophore
s. The most common iterative
algorithm for the purpose is the Richardson–Lucy deconvolution algorithm; the Wiener deconvolution
(and approximations) are the most common non-iterative algorithms.
, a specific kind of radio astronomy
, one step consists of deconvolving the produced image with the "dirty beam", which is a different name for the point spread function
. A common used method is the CLEAN algorithm
.
Tutorials and techniques
Software
Other
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, deconvolution is an algorithm-based
Algorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
process used to reverse the effects of convolution
Convolution
In mathematics and, in particular, functional analysis, convolution is a mathematical operation on two functions f and g, producing a third function that is typically viewed as a modified version of one of the original functions. Convolution is similar to cross-correlation...
on recorded data. The concept of deconvolution is widely used in the techniques of signal processing
Signal processing
Signal processing is an area of systems engineering, electrical engineering and applied mathematics that deals with operations on or analysis of signals, in either discrete or continuous time...
and image processing
Image processing
In electrical engineering and computer science, image processing is any form of signal processing for which the input is an image, such as a photograph or video frame; the output of image processing may be either an image or, a set of characteristics or parameters related to the image...
. Because these techniques are in turn widely used in many scientific
Science
Science is a systematic enterprise that builds and organizes knowledge in the form of testable explanations and predictions about the universe...
and engineering
Engineering
Engineering is the discipline, art, skill and profession of acquiring and applying scientific, mathematical, economic, social, and practical knowledge, in order to design and build structures, machines, devices, systems, materials and processes that safely realize improvements to the lives of...
disciplines, deconvolution finds many applications.
In general, the object of deconvolution is to find the solution of a convolution equation of the form:
Usually, h is some recorded signal, and ƒ is some signal that we wish to recover, but has been convolved with some other signal g before we recorded it. The function g might represent the transfer function
Transfer function
A transfer function is a mathematical representation, in terms of spatial or temporal frequency, of the relation between the input and output of a linear time-invariant system. With optical imaging devices, for example, it is the Fourier transform of the point spread function i.e...
of an instrument or a driving force that was applied to a physical system. If we know g, or at least know the form of g, then we can perform deterministic deconvolution. However, if we do not know g in advance, then we need to estimate it. This is most often done using methods of statistical
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
estimation
Estimation theory
Estimation theory is a branch of statistics and signal processing that deals with estimating the values of parameters based on measured/empirical data that has a random component. The parameters describe an underlying physical setting in such a way that their value affects the distribution of the...
.
In physical measurements, the situation is usually closer to
In this case ε is noise that has entered our recorded signal. If we assume that a noisy signal or image is noiseless when we try to make a statistical estimate of g, our estimate will be incorrect. In turn, our estimate of ƒ will also be incorrect. The lower the signal-to-noise ratio
Signal-to-noise ratio
Signal-to-noise ratio is a measure used in science and engineering that compares the level of a desired signal to the level of background noise. It is defined as the ratio of signal power to the noise power. A ratio higher than 1:1 indicates more signal than noise...
, the worse our estimate of the deconvolved signal will be. That is the reason why usually inverse filter
Inverse filter
In all proposed models for the production of human speech, an important variable is the waveform of the airflow, or volume velocity, at the glottis. The glottal volume velocity waveform provides the link between movements of the vocal folds and the acoustical results of such movements, in that the...
ing the signal is not a good solution. However, if we have at least some knowledge of the type of noise in the data (for example, white noise
White noise
White noise is a random signal with a flat power spectral density. In other words, the signal contains equal power within a fixed bandwidth at any center frequency...
), we may be able to improve the estimate of ƒ through techniques such as Wiener deconvolution
Wiener deconvolution
In mathematics, Wiener deconvolution is an application of the Wiener filter to the noise problems inherent in deconvolution. It works in the frequency domain, attempting to minimize the impact of deconvoluted noise at frequencies which have a poor signal-to-noise ratio.The Wiener deconvolution...
.
The foundations for deconvolution and time-series analysis were largely laid by Norbert Wiener
Norbert Wiener
Norbert Wiener was an American mathematician.A famous child prodigy, Wiener later became an early researcher in stochastic and noise processes, contributing work relevant to electronic engineering, electronic communication, and control systems.Wiener is regarded as the originator of cybernetics, a...
of the Massachusetts Institute of Technology
Massachusetts Institute of Technology
The Massachusetts Institute of Technology is a private research university located in Cambridge, Massachusetts. MIT has five schools and one college, containing a total of 32 academic departments, with a strong emphasis on scientific and technological education and research.Founded in 1861 in...
in his book Extrapolation, Interpolation, and Smoothing of Stationary Time Series (1949). The book was based on work Wiener had done during World War II
World War II
World War II, or the Second World War , was a global conflict lasting from 1939 to 1945, involving most of the world's nations—including all of the great powers—eventually forming two opposing military alliances: the Allies and the Axis...
but that had been classified at the time. Some of the early attempts to apply these theories were in the fields of weather forecasting
Weather forecasting
Weather forecasting is the application of science and technology to predict the state of the atmosphere for a given location. Human beings have attempted to predict the weather informally for millennia, and formally since the nineteenth century...
and economics
Economics
Economics is the social science that analyzes the production, distribution, and consumption of goods and services. The term economics comes from the Ancient Greek from + , hence "rules of the house"...
.
Seismology
The concept of deconvolution had an early application in reflection seismologyReflection seismology
Reflection seismology is a method of exploration geophysics that uses the principles of seismology to estimate the properties of the Earth's subsurface from reflected seismic waves. The method requires a controlled seismic source of energy, such as dynamite/Tovex, a specialized air gun or a...
. In 1950, Enders Robinson was a graduate student at MIT. He worked with others at MIT, such as Norbert Wiener
Norbert Wiener
Norbert Wiener was an American mathematician.A famous child prodigy, Wiener later became an early researcher in stochastic and noise processes, contributing work relevant to electronic engineering, electronic communication, and control systems.Wiener is regarded as the originator of cybernetics, a...
, Norman Levinson
Norman Levinson
Norman Levinson was an American mathematician. Some of his major contributions were in the study of Fourier transforms, complex analysis, non-linear differential equations, number theory, and signal processing. He worked closely with Norbert Wiener in his early career...
, and economist Paul Samuelson
Paul Samuelson
Paul Anthony Samuelson was an American economist, and the first American to win the Nobel Memorial Prize in Economic Sciences. The Swedish Royal Academies stated, when awarding the prize, that he "has done more than any other contemporary economist to raise the level of scientific analysis in...
, to develop the "convolutional model" of a reflection seismogram. This model assumes that the recorded seismogram
Seismogram
A seismogram is a graph output by a seismograph. It is a record of the ground motion at a measuring station as a function of time. Seismograms typically record motions in three cartesian axes , with the z axis perpendicular to the Earth's surface and the x- and y- axes parallel to the surface...
s(t) is the convolution of an Earth-reflectivity function e(t) and a seismic wavelet w(t) from a point source
Point source
A point source is a localised, relatively small source of something.Point source may also refer to:*Point source , a localised source of pollution**Point source water pollution, water pollution with a localized source...
, where t represents recording time. Thus, our convolution equation is
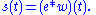
The seismologist is interested in e, which contains information about the Earth's structure. By the convolution theorem
Convolution theorem
In mathematics, the convolution theorem states that under suitableconditions the Fourier transform of a convolution is the pointwise product of Fourier transforms. In other words, convolution in one domain equals point-wise multiplication in the other domain...
, this equation may be Fourier transform
Fourier transform
In mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...
ed to
in the frequency domain
Frequency domain
In electronics, control systems engineering, and statistics, frequency domain is a term used to describe the domain for analysis of mathematical functions or signals with respect to frequency, rather than time....
. By assuming that the reflectivity is white, we can assume that the power spectrum
Spectral density
In statistical signal processing and physics, the spectral density, power spectral density , or energy spectral density , is a positive real function of a frequency variable associated with a stationary stochastic process, or a deterministic function of time, which has dimensions of power per hertz...
of the reflectivity is constant, and that the power spectrum of the seismogram is the spectrum of the wavelet multiplied by that constant. Thus,
If we assume that the wavelet is minimum phase
Minimum phase
In control theory and signal processing, a linear, time-invariant system is said to be minimum-phase if the system and its inverse are causal and stable....
, we can recover it by calculating the minimum phase equivalent of the power spectrum we just found. The reflectivity may be recovered by designing and applying a Wiener filter
Wiener filter
In signal processing, the Wiener filter is a filter proposed by Norbert Wiener during the 1940s and published in 1949. Its purpose is to reduce the amount of noise present in a signal by comparison with an estimation of the desired noiseless signal. The discrete-time equivalent of Wiener's work was...
that shapes the estimated wavelet to a Dirac delta function
Dirac delta function
The Dirac delta function, or δ function, is a generalized function depending on a real parameter such that it is zero for all values of the parameter except when the parameter is zero, and its integral over the parameter from −∞ to ∞ is equal to one. It was introduced by theoretical...
(i.e., a spike). The result may be seen as a series of scaled, shifted delta functions (although this is not mathematically rigorous):
-
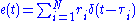 ,
,
where N is the number of reflection events, τ i τ i are the reflection times of each event, and r i are the reflection coefficient
Reflection coefficient
The reflection coefficient is used in physics and electrical engineering when wave propagation in a medium containing discontinuities is considered. A reflection coefficient describes either the amplitude or the intensity of a reflected wave relative to an incident wave...
s.
In practice, since we are dealing with noisy, finite bandwidth
Bandwidth (computing)
In computer networking and computer science, bandwidth, network bandwidth, data bandwidth, or digital bandwidth is a measure of available or consumed data communication resources expressed in bits/second or multiples of it .Note that in textbooks on wireless communications, modem data transmission,...
, finite length, discretely sampled datasets, the above procedure only yields an approximation of the filter required to deconvolve the data. However, by formulating the problem as the solution of a Toeplitz matrix
Toeplitz matrix
In linear algebra, a Toeplitz matrix or diagonal-constant matrix, named after Otto Toeplitz, is a matrix in which each descending diagonal from left to right is constant...
and using Levinson recursion
Levinson recursion
Levinson recursion or Levinson-Durbin recursion is a procedure in linear algebra to recursively calculate the solution to an equation involving a Toeplitz matrix...
, we can relatively quickly estimate a filter with the smallest mean squared error
Mean squared error
In statistics, the mean squared error of an estimator is one of many ways to quantify the difference between values implied by a kernel density estimator and the true values of the quantity being estimated. MSE is a risk function, corresponding to the expected value of the squared error loss or...
possible. We can also do deconvolution directly in the frequency domain and get similar results. The technique is closely related to linear prediction
Linear prediction
Linear prediction is a mathematical operation where future values of a discrete-time signal are estimated as a linear function of previous samples....
.
Optics and other imaging
In optics and imaging, the term "deconvolution" is specifically used to refer to the process of reversing the optical distortion that takes place in an optical microscopeMicroscope
A microscope is an instrument used to see objects that are too small for the naked eye. The science of investigating small objects using such an instrument is called microscopy...
, electron microscope
Electron microscope
An electron microscope is a type of microscope that uses a beam of electrons to illuminate the specimen and produce a magnified image. Electron microscopes have a greater resolving power than a light-powered optical microscope, because electrons have wavelengths about 100,000 times shorter than...
, telescope
Telescope
A telescope is an instrument that aids in the observation of remote objects by collecting electromagnetic radiation . The first known practical telescopes were invented in the Netherlands at the beginning of the 1600s , using glass lenses...
, or other imaging instrument, thus creating clearer images. It is usually done in the digital domain by a software algorithm
Algorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
, as part of a suite of microscope image processing
Microscope image processing
Microscope image processing is a broad term that covers the use of digital image processing techniques to process, analyze and present images obtained from a microscope. Such processing is now commonplace in a number of diverse fields such as medicine, biological research, cancer research, drug...
techniques. Deconvolution is also practical to sharpen images that suffer from fast motion or jiggles during capturing. Early Hubble Space Telescope
Hubble Space Telescope
The Hubble Space Telescope is a space telescope that was carried into orbit by a Space Shuttle in 1990 and remains in operation. A 2.4 meter aperture telescope in low Earth orbit, Hubble's four main instruments observe in the near ultraviolet, visible, and near infrared...
images were distorted by a flawed mirror and could be sharpened by deconvolution.
The usual method is to assume that the optical path through the instrument is optically perfect, convolved with a point spread function
Point spread function
The point spread function describes the response of an imaging system to a point source or point object. A more general term for the PSF is a system's impulse response, the PSF being the impulse response of a focused optical system. The PSF in many contexts can be thought of as the extended blob...
(PSF), that is, a mathematical function that describes the distortion in terms of the pathway a theoretical point source
Point source
A point source is a localised, relatively small source of something.Point source may also refer to:*Point source , a localised source of pollution**Point source water pollution, water pollution with a localized source...
of light (or other waves) takes through the instrument. Usually, such a point source contributes a small area of fuzziness to the final image. If this function can be determined, it is then a matter of computing its inverse
Inverse function
In mathematics, an inverse function is a function that undoes another function: If an input x into the function ƒ produces an output y, then putting y into the inverse function g produces the output x, and vice versa. i.e., ƒ=y, and g=x...
or complementary function, and convolving the acquired image with that. The result is the original, undistorted image.
In practice, finding the true PSF is impossible, and usually an approximation of it is used, theoretically calculated or based on some experimental estimation by using known probes. Real optics may also have different PSFs at different focal and spatial locations, and the PSF may be non-linear. The accuracy of the approximation of the PSF will dictate the final result. Different algorithms can be employed to give better results, at the price of being more computationally intensive. Since the original convolution discards data, some algorithms use additional data acquired at nearby focal points to make up some of the lost information. Regularization
Regularization (mathematics)
In mathematics and statistics, particularly in the fields of machine learning and inverse problems, regularization involves introducing additional information in order to solve an ill-posed problem or to prevent overfitting...
in iterative algorithms (as in expectation-maximization algorithm
Expectation-maximization algorithm
In statistics, an expectation–maximization algorithm is an iterative method for finding maximum likelihood or maximum a posteriori estimates of parameters in statistical models, where the model depends on unobserved latent variables...
s) can be applied to avoid unrealistic solutions.
When the PSF is unknown, it may be possible to deduce it by systematically trying different possible PSFs and assessing whether the image has improved. This procedure is called blind deconvolution
Blind deconvolution
In image processing and applied mathematics, blind deconvolution is a deconvolution technique that permits recovery of the target scene from a single or set of "blurred" images in the presence of a poorly determined or unknown point spread function ....
. Blind deconvolution is a well-established image restoration technique in astronomy
Astronomy
Astronomy is a natural science that deals with the study of celestial objects and phenomena that originate outside the atmosphere of Earth...
, where the point nature of the objects photographed exposes the PSF thus making it more feasible. It is also used in fluorescence microscopy for image restoration, and in fluorescence spectral imaging
Spectral imaging
Spectral imaging is a branch of spectroscopy and of photography in which a complete spectrum or some spectral information is collected at every location in an image plane...
for spectral separation of multiple unknown fluorophore
Fluorophore
A fluorophore, in analogy to a chromophore, is a component of a molecule which causes a molecule to be fluorescent. It is a functional group in a molecule which will absorb energy of a specific wavelength and re-emit energy at a different wavelength...
s. The most common iterative
Iteration
Iteration means the act of repeating a process usually with the aim of approaching a desired goal or target or result. Each repetition of the process is also called an "iteration," and the results of one iteration are used as the starting point for the next iteration.-Mathematics:Iteration in...
algorithm for the purpose is the Richardson–Lucy deconvolution algorithm; the Wiener deconvolution
Wiener deconvolution
In mathematics, Wiener deconvolution is an application of the Wiener filter to the noise problems inherent in deconvolution. It works in the frequency domain, attempting to minimize the impact of deconvoluted noise at frequencies which have a poor signal-to-noise ratio.The Wiener deconvolution...
(and approximations) are the most common non-iterative algorithms.
Radio astronomy
When performing image synthesis in radio interferometryInterferometry
Interferometry refers to a family of techniques in which electromagnetic waves are superimposed in order to extract information about the waves. An instrument used to interfere waves is called an interferometer. Interferometry is an important investigative technique in the fields of astronomy,...
, a specific kind of radio astronomy
Radio astronomy
Radio astronomy is a subfield of astronomy that studies celestial objects at radio frequencies. The initial detection of radio waves from an astronomical object was made in the 1930s, when Karl Jansky observed radiation coming from the Milky Way. Subsequent observations have identified a number of...
, one step consists of deconvolving the produced image with the "dirty beam", which is a different name for the point spread function
Point spread function
The point spread function describes the response of an imaging system to a point source or point object. A more general term for the PSF is a system's impulse response, the PSF being the impulse response of a focused optical system. The PSF in many contexts can be thought of as the extended blob...
. A common used method is the CLEAN algorithm
CLEAN (algorithm)
The CLEAN algorithm is a computational algorithm to perform a deconvolution on images created in radio astronomy. It was published by Jan Högbom in 1974 and several variations have been proposed since then ....
.
See also
- Digital filterDigital filterIn electronics, computer science and mathematics, a digital filter is a system that performs mathematical operations on a sampled, discrete-time signal to reduce or enhance certain aspects of that signal. This is in contrast to the other major type of electronic filter, the analog filter, which is...
- Filter (signal processing)Filter (signal processing)In signal processing, a filter is a device or process that removes from a signal some unwanted component or feature. Filtering is a class of signal processing, the defining feature of filters being the complete or partial suppression of some aspect of the signal...
- Filter designFilter designFilter design is the process of designing a filter , often a linear shift-invariant filter, that satisfies a set of requirements, some of which are contradictory...
- Minimum phaseMinimum phaseIn control theory and signal processing, a linear, time-invariant system is said to be minimum-phase if the system and its inverse are causal and stable....
- Independent component analysisIndependent component analysisIndependent component analysis is a computational method for separating a multivariate signal into additive subcomponents supposing the mutual statistical independence of the non-Gaussian source signals...
- Wiener deconvolutionWiener deconvolutionIn mathematics, Wiener deconvolution is an application of the Wiener filter to the noise problems inherent in deconvolution. It works in the frequency domain, attempting to minimize the impact of deconvoluted noise at frequencies which have a poor signal-to-noise ratio.The Wiener deconvolution...
- Richardson–Lucy deconvolution
- Digital room correctionDigital room correctionDigital room correction is a process in the field of acoustics where digital filters designed to ameliorate unfavorable effects of a room's acoustics are applied to the input of a sound reproduction system...
- Free deconvolutionFree deconvolutionFree convolution is the free probability analog of the classical notion of convolution of probability measures. Due to the non-commutative nature of free probability theory, one has to talk separately about additive and multiplicative free convolution, which arise from addition and multiplication...
- Point spread functionPoint spread functionThe point spread function describes the response of an imaging system to a point source or point object. A more general term for the PSF is a system's impulse response, the PSF being the impulse response of a focused optical system. The PSF in many contexts can be thought of as the extended blob...
External links
Presentations- Use of a deconvolution process to cancel complex motion/shake in photography(in French) next and results by JM Pichot Many photos, and no math!(in French)
- Flash presentation of blind deconvolution and source separation problem
- 3D simulations of deconvolution applied to Digital Room Correction
- Deconvolution Explanation and Examples
Tutorials and techniques
- Deconvolution in optical microscopy
- A summary of blind deconvolution techniques.
- BiophotonicsBiophotonicsThe term biophotonics denotes a combination of biology and photonics, with photonics being the science and technology of generation, manipulation, and detection of photons, quantum units of light. Photonics is related to electronics in that it is believed that photons will play a similar central...
article on deconvolution (PDF) - Deconvolution Tutorial
Software
- Mathematica ImageDeconvolve function
- Mathematica ListDeconvolve function
- Focus Magic, Software that uses deconvolution to fix out-of-focus blur and motion blur in an image
- Unshake, a blind deconvolver Java program for terrestrial photographs (currently freeware)
- SVI-wiki on 3D microscopy and deconvolution
- Tria Image Processing, Applies deconvolution and blind deconvolution to quickly remove blur from images
- DeblurMyImage from ADPTools - uses state-of-art deconvolution methods for out-of-focus correction and motion correction
- bitplaneBitplaneBitplane is a provider of software for 3D and 4D image analysis for the life sciences. Founded in December 1992, Bitplane operates out of two offices in Zürich, Switzerland and one in South Windor, CT, USA.- Company history :...
Other