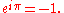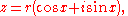De Moivre's formula
Encyclopedia
In mathematics
, de Moivre's formula (a.k.a. De Moivre's theorem), named after Abraham de Moivre
, states that for any complex number
(and, in particular, for any real number
) x and integer
n it holds that
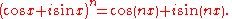
The formula is important because it connects complex numbers (i stands for the imaginary unit
(i=√-1)) and trigonometry
. The expression cos x + i sin x is sometimes abbreviated to cis x.
By expanding the left hand side and then comparing the real and imaginary parts under the assumption that x is real, it is possible to derive useful expressions for cos (nx) and sin (nx) in terms of cos x and sin x. Furthermore, one can use a generalization of this formula to find explicit expressions for the nth roots of unity
, that is, complex numbers z such that zn = 1.
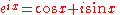
and the exponential law
for integer powers

Then, by Euler's formula
,
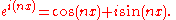
The derivation of de Moivre's formula above involves a complex number to the power n. When the power is not an integer, the result is multiple-valued, for example, when n = ½ then:
Since the angles 0 and 2π are the same this would give two different values for the same expression. The values 1 and −1 are however both square roots of 1 as the generalization asserts.
No such problem occurs with Euler's formula since there is no identification of different values of its exponent. Euler's formula involves a complex power of a positive real number and this always has a defined value. The corresponding expressions are:

For n > 0, we proceed by mathematical induction
. S(1) is clearly true. For our hypothesis, we assume S(k) is true for some natural k. That is, we assume
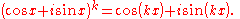
Now, considering S(k+1):
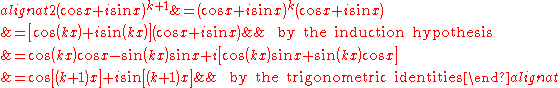
We deduce that S(k) implies S(k+1). By the principle of mathematical induction it follows that the result is true for all natural numbers. Now, S(0) is clearly true since cos (0x) + i sin(0x) = 1 +i 0 = 1. Finally, for the negative integer cases, we consider an exponent of -n for natural n.
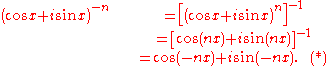
The equation (*) is a result of the identity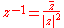 , for z = cos nx + i sin nx. Hence, S(n) holds for all integers n.
, for z = cos nx + i sin nx. Hence, S(n) holds for all integers n.
s, one necessarily has equality both of the real parts and of the imaginary parts of both members of the equation. If x, and therefore also cos x and sin x, are real number
s, then the identity of these parts can be written using binomial coefficient
s. This formula was given by 16th century French mathematician Franciscus Vieta:
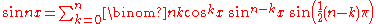
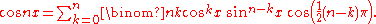
In each of these two equations, the final trigonometric function equals one or minus one or zero, thus removing half the entries in each of the sums. These equations are in fact even valid for complex values of x, because both sides are entire
(that is, holomorphic on the whole complex plane
) functions of x, and two such functions that coincide on the real axis necessarily coincide everywhere. Here are the concrete instances of these equations for n = 2 and n = 3:
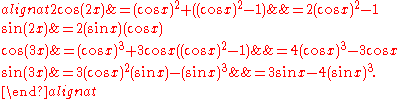
The right hand side of the formula for cos(nx) is in fact the value Tn(cos x) of the Chebyshev polynomial Tn at cos x.
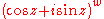
is a multi-valued function while

is not. Therefore one can state that
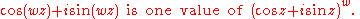
of a complex number. This application does not strictly use de Moivre's formula as the power isn't an integer. However considering the right hand side to the power of n will in each case give the same value left hand side.
If z is a complex number, written in polar form as
then
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, de Moivre's formula (a.k.a. De Moivre's theorem), named after Abraham de Moivre
Abraham de Moivre
Abraham de Moivre was a French mathematician famous for de Moivre's formula, which links complex numbers and trigonometry, and for his work on the normal distribution and probability theory. He was a friend of Isaac Newton, Edmund Halley, and James Stirling...
, states that for any complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
(and, in particular, for any real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
) x and integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
n it holds that
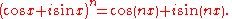
The formula is important because it connects complex numbers (i stands for the imaginary unit
Imaginary unit
In mathematics, the imaginary unit allows the real number system ℝ to be extended to the complex number system ℂ, which in turn provides at least one root for every polynomial . The imaginary unit is denoted by , , or the Greek...
(i=√-1)) and trigonometry
Trigonometric function
In mathematics, the trigonometric functions are functions of an angle. They are used to relate the angles of a triangle to the lengths of the sides of a triangle...
. The expression cos x + i sin x is sometimes abbreviated to cis x.
By expanding the left hand side and then comparing the real and imaginary parts under the assumption that x is real, it is possible to derive useful expressions for cos (nx) and sin (nx) in terms of cos x and sin x. Furthermore, one can use a generalization of this formula to find explicit expressions for the nth roots of unity
Root of unity
In mathematics, a root of unity, or de Moivre number, is any complex number that equals 1 when raised to some integer power n. Roots of unity are used in many branches of mathematics, and are especially important in number theory, the theory of group characters, field theory, and the discrete...
, that is, complex numbers z such that zn = 1.
Derivation
Although historically proven earlier, de Moivre's formula can easily be derived from Euler's formula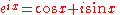
and the exponential law
Exponentiation
Exponentiation is a mathematical operation, written as an, involving two numbers, the base a and the exponent n...
for integer powers

Then, by Euler's formula
Euler's formula
Euler's formula, named after Leonhard Euler, is a mathematical formula in complex analysis that establishes the deep relationship between the trigonometric functions and the complex exponential function...
,
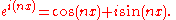
Failure for non-integer powers
De Moivre's formula does not in general hold for non-integer powers. Non-integer powers of a complex number can have many different values, see failure of power and logarithm identities. However there is a generalization that the right hand side expression is one possible value of the power.The derivation of de Moivre's formula above involves a complex number to the power n. When the power is not an integer, the result is multiple-valued, for example, when n = ½ then:
- For x = 0 the formula gives 1½ = 1
- For x = 2π the formula gives 1½ = −1.
Since the angles 0 and 2π are the same this would give two different values for the same expression. The values 1 and −1 are however both square roots of 1 as the generalization asserts.
No such problem occurs with Euler's formula since there is no identification of different values of its exponent. Euler's formula involves a complex power of a positive real number and this always has a defined value. The corresponding expressions are:
Proof by induction (for integer n)
The truth of de Moivre's theorem can be established by mathematical induction for natural numbers, and extended to all integers from there. Consider S(n):
For n > 0, we proceed by mathematical induction
Mathematical induction
Mathematical induction is a method of mathematical proof typically used to establish that a given statement is true of all natural numbers...
. S(1) is clearly true. For our hypothesis, we assume S(k) is true for some natural k. That is, we assume
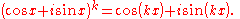
Now, considering S(k+1):
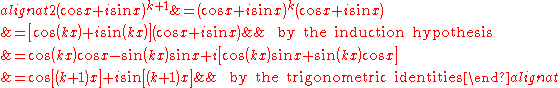
We deduce that S(k) implies S(k+1). By the principle of mathematical induction it follows that the result is true for all natural numbers. Now, S(0) is clearly true since cos (0x) + i sin(0x) = 1 +i 0 = 1. Finally, for the negative integer cases, we consider an exponent of -n for natural n.
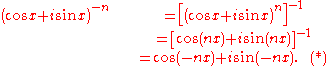
The equation (*) is a result of the identity
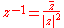 , for z = cos nx + i sin nx. Hence, S(n) holds for all integers n.
, for z = cos nx + i sin nx. Hence, S(n) holds for all integers n.Formulas for cosine and sine individually
Being an equality of complex numberComplex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s, one necessarily has equality both of the real parts and of the imaginary parts of both members of the equation. If x, and therefore also cos x and sin x, are real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s, then the identity of these parts can be written using binomial coefficient
Binomial coefficient
In mathematics, binomial coefficients are a family of positive integers that occur as coefficients in the binomial theorem. They are indexed by two nonnegative integers; the binomial coefficient indexed by n and k is usually written \tbinom nk , and it is the coefficient of the x k term in...
s. This formula was given by 16th century French mathematician Franciscus Vieta:
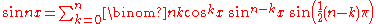
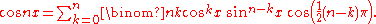
In each of these two equations, the final trigonometric function equals one or minus one or zero, thus removing half the entries in each of the sums. These equations are in fact even valid for complex values of x, because both sides are entire
Entire function
In complex analysis, an entire function, also called an integral function, is a complex-valued function that is holomorphic over the whole complex plane...
(that is, holomorphic on the whole complex plane
Complex plane
In mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis...
) functions of x, and two such functions that coincide on the real axis necessarily coincide everywhere. Here are the concrete instances of these equations for n = 2 and n = 3:
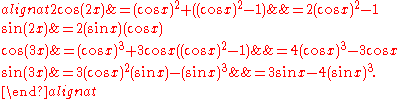
The right hand side of the formula for cos(nx) is in fact the value Tn(cos x) of the Chebyshev polynomial Tn at cos x.
Generalization
The formula is actually true in a more general setting than stated above: if z and w are complex numbers, then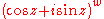
is a multi-valued function while

is not. Therefore one can state that
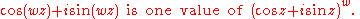
Applications
This formula can be used to find the nth rootsNth root
In mathematics, the nth root of a number x is a number r which, when raised to the power of n, equals xr^n = x,where n is the degree of the root...
of a complex number. This application does not strictly use de Moivre's formula as the power isn't an integer. However considering the right hand side to the power of n will in each case give the same value left hand side.
If z is a complex number, written in polar form as
then
-

where k is an integer. To get the n different roots of z one only needs to consider values of k from 0 to n − 1.
External links
- De Moivre's Theorem for Trig Identities by Michael Croucher, Wolfram Demonstrations ProjectWolfram Demonstrations ProjectThe Wolfram Demonstrations Project is hosted by Wolfram Research, whose stated goal is to bring computational exploration to the widest possible audience. It consists of an organized, open-source collection of small interactive programs called Demonstrations, which are meant to visually and...
.
- De Moivre's Theorem for Trig Identities by Michael Croucher, Wolfram Demonstrations Project