
Cyclic redundancy check
Encyclopedia
A cyclic redundancy check (CRC) is an error-detecting code
commonly used in digital networks
and storage devices to detect accidental changes to raw data. Blocks of data entering these systems get a short check value attached, based on the remainder of a polynomial division
of their contents; on retrieval the calculation is repeated, and corrective action can be taken against presumed data corruption if the check values do not match.
CRCs are so called because the check (data verification) value is a redundancy (it adds no information to the message) and the algorithm
is based on cyclic codes. CRCs are popular because they are simple to implement in binary hardware
, easy to analyze mathematically, and particularly good at detecting common errors caused by noise
in transmission channels. Because the check value has a fixed length, the function
that generates it is occasionally used as a hash function
. The CRC was invented by W. Wesley Peterson
in 1961; the 32-bit polynomial used in the CRC function of Ethernet and many other standards is the work of several researchers and was published in 1975.
cyclic codes, which encode messages by adding a fixed-length check value, for the purpose of error detection in communication networks was first proposed by W. Wesley Peterson
in 1961.
Cyclic codes are not only simple to implement but have the benefit of being particularly well suited for the detection of burst errors, contiguous sequences of erroneous data symbols in messages. This is important because burst errors are common transmission errors in many communication channels, including magnetic and optical storage devices. Typically an n-bit CRC applied to a data block of arbitrary length, will detect any single error burst not longer than n bits and will detect a fraction 1−2−n of all longer error bursts.
Specification of a CRC code requires definition of a so-called generator polynomial. This polynomial resembles the divisor
in a polynomial long division
, which takes the message as the dividend
and in which the quotient
is discarded and the remainder
becomes the result, with the important distinction that the polynomial coefficient
s are calculated according to the carry-less arithmetic of a finite field
. The length of the remainder is always less than the length of the generator polynomial, which therefore determines how long the result can be.
In practice, all commonly used CRCs employ the finite field GF(2)
. This is the field of two elements, usually called 0 and 1, comfortably matching computer architecture. The rest of this article will discuss only these binary CRCs, but the principles are more general.
The simplest error-detection system, the parity bit
, is in fact a trivial 1-bit CRC: it uses the generator polynomial x+1.
of messages delivered. However, they are not suitable for protecting against intentional alteration of data. Firstly, as there is no authentication, an attacker can edit a message and recalculate the CRC without the substitution being detected. This is even the case when the CRC is encrypted, leading to one of the design flaws of the WEP
protocol. Secondly, the linear
properties of CRC codes even allow an attacker to modify a message in such a way as to leave the check value unchanged, and otherwise permit efficient recalculation of the CRC for compact changes. Nonetheless, it is still often falsely assumed that when a message and its correct check value are received from an open channel then the message cannot have been altered in transit.
Cryptographic hash function
s, while still not providing security against intentional alteration when used in this manner, can provide stronger error checking in that they do not rely on specific error pattern assumptions. However, they are much slower than CRCs, and are therefore commonly used to protect off-line data, such as files on servers or databases.
When stored alongside the data, CRCs and cryptographic hash functions by themselves do not protect against intentional modification of data. Any application that requires protection against such attacks must use cryptographic authentication mechanisms, such as message authentication code
s.
") underneath the left-hand end of the row.
Start with the message to be encoded:
This is first padded with zeroes corresponding to the bit length n of the CRC. Here is the first calculation for computing a 3-bit CRC:
If the input bit above the leftmost divisor bit is 0, do nothing. If the input bit above the leftmost divisor bit is 1, the divisor is XORed into the input (in other words, the input bit above each 1-bit in the divisor is toggled). The divisor is then shifted one bit to the right, and the process is repeated until the divisor reaches the right-hand end of the input row. Here is the entire calculation:
Since the leftmost divisor bit zeroed every input bit it touched, when this process ends the only bits in the input row that can be nonzero are the n bits at the right-hand end of the row. These n bits are the remainder of the division step, and will also be the value of the CRC function (unless the chosen CRC specification calls for some postprocessing).
The validity of a received message can easily be verified by performing the above calculation again, this time with the check value added instead of zeroes. The remainder should equal zero if there are no detectable errors.
instead of more familiar numbers. This binary polynomial is treated as a ring
. A ring is, loosely speaking, a set of elements somewhat like numbers, that can be operated on by an operation that somewhat resembles addition and another operation that somewhat resembles multiplication, these operations possessing many of the familiar arithmetic properties of commutativity, associativity, and distributivity. Ring theory is part of abstract algebra
.
The most important attribute of the polynomial is its length (largest degree(exponent) +1 of any one term in the polynomial), because of its direct influence on the length of the computed check value.
The most commonly used polynomial lengths are:
The design of the CRC polynomial depends on the maximum total length of the block to be protected (data + CRC bits), the desired error protection features, and the type of resources for implementing the CRC as well as the desired performance. A common misconception is that the "best" CRC polynomials are derived from either an irreducible polynomial
or an irreducible polynomial times the factor , which adds to the code the ability to detect all errors affecting an odd number of bits. In reality, all the factors described above should enter in the selection of the polynomial. However, choosing a non-irreducible polynomial can result in missed errors due to the ring having zero divisor
, which adds to the code the ability to detect all errors affecting an odd number of bits. In reality, all the factors described above should enter in the selection of the polynomial. However, choosing a non-irreducible polynomial can result in missed errors due to the ring having zero divisor
s.
The advantage of choosing a primitive polynomial
as the generator for a CRC code is that the resulting code has maximal total block length; in here if r is the degree of the primitive generator polynomial then the maximal total blocklength is equal to , and the associated code is able to detect any single bit or double errors. If instead, we used as generator polynomial
, and the associated code is able to detect any single bit or double errors. If instead, we used as generator polynomial 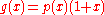 , where
, where 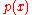 is a primitive polynomial of degree
is a primitive polynomial of degree  , then the maximal total blocklength would be equal to
, then the maximal total blocklength would be equal to 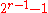 but the code would be able to detect single, double, and triple errors.
but the code would be able to detect single, double, and triple errors.
A polynomial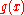 that admits other factorizations may be chosen then so as to balance the maximal total blocklength with a desired error detection power. A powerful class of such polynomials, which subsumes the two examples described above, is that of BCH code
that admits other factorizations may be chosen then so as to balance the maximal total blocklength with a desired error detection power. A powerful class of such polynomials, which subsumes the two examples described above, is that of BCH code
s. Regardless of the reducibility properties of a generator polynomial of degree r, assuming that it includes the "+1" term, such error detection code will be able to detect all error patterns that are confined to a window of r contiguous bits. These patterns are called "error bursts".
These complications mean that there are three common ways to express a polynomial as an integer: the first two, which are mirror images in binary, are the constants found in code; the third is the number found in Koopman's papers. In each case, one term is omitted. So the polynomial may be transcribed as:
may be transcribed as:
In the table below they are shown as:
The polynomials commonly applied are not the most efficient ones possible. Between 1993 and 2004, Koopman, Castagnoli and others surveyed the space of polynomials up to 16 bits, and of 24 and 32 bits, finding examples that have much better performance (in terms of Hamming distance
for a given message size) than the polynomials of earlier protocols, and publishing the best of these with the aim of improving the error detection capacity of future standards. In particular, iSCSI
and SCTP have adopted one of the findings of this research, the CRC-32C (Castagnoli) polynomial.
The design of the 32-bit polynomial most commonly used by standards bodies, CRC-32-IEEE, was the result of a joint effort for the Rome Laboratory
and the Air Force Electronic Systems Division by Joseph Hammond, James Brown and Shyan-Shiang Liu of the Georgia Institute of Technology
and Kenneth Brayer of the MITRE
Corporation. The earliest known appearances of the 32-bit polynomial were in their 1975 publications: Technical Report 2956 by Brayer for MITRE, published in January and released for public dissemination through DTIC in August, and Hammond, Brown and Liu's report for the Rome Laboratory, published in May. Both reports contained contributions from the other team. In December 1975, Brayer and Hammond presented their work in a paper at the IEEE National Telecommunications Conference: the IEEE CRC-32 polynomial is the generating polynomial of a Hamming code
and was selected for its error detection performance. Even so, the Castagnoli CRC-32C polynomial used in iSCSI or SCTP matches its performance on messages from 58 bits–131 kbits, and outperforms it in several size ranges including the two most common sizes of Internet packet. The ITU-T
G.hn
standard also uses CRC-32C to detect errors in the payload (although it uses CRC-16-CCITT for PHY headers).
The table below lists only the polynomials of the various algorithms in use. Variations of a particular protocol can impose pre-inversion, post-inversion and reversed bit ordering as described above. For example, the CRC32 used in both Gzip and Bzip2 use the same polynomial, but Bzip2 employs reversed bit ordering, while Gzip does not.
CRCs in proprietary protocols might use a non-trivial initial value and final XOR for obfuscation
but this does not add cryptographic strength to the algorithm. An unknown error-detecting code can be characterized as a CRC, and as such fully reverse-engineered
, from its output codewords.
Error detection and correction
In information theory and coding theory with applications in computer science and telecommunication, error detection and correction or error control are techniques that enable reliable delivery of digital data over unreliable communication channels...
commonly used in digital networks
Telecommunications network
A telecommunications network is a collection of terminals, links and nodes which connect together to enable telecommunication between users of the terminals. Networks may use circuit switching or message switching. Each terminal in the network must have a unique address so messages or connections...
and storage devices to detect accidental changes to raw data. Blocks of data entering these systems get a short check value attached, based on the remainder of a polynomial division
Polynomial long division
In algebra, polynomial long division is an algorithm for dividing a polynomial by another polynomial of the same or lower degree, a generalised version of the familiar arithmetic technique called long division...
of their contents; on retrieval the calculation is repeated, and corrective action can be taken against presumed data corruption if the check values do not match.
CRCs are so called because the check (data verification) value is a redundancy (it adds no information to the message) and the algorithm
Algorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
is based on cyclic codes. CRCs are popular because they are simple to implement in binary hardware
Computer hardware
Personal computer hardware are component devices which are typically installed into or peripheral to a computer case to create a personal computer upon which system software is installed including a firmware interface such as a BIOS and an operating system which supports application software that...
, easy to analyze mathematically, and particularly good at detecting common errors caused by noise
Noise
In common use, the word noise means any unwanted sound. In both analog and digital electronics, noise is random unwanted perturbation to a wanted signal; it is called noise as a generalisation of the acoustic noise heard when listening to a weak radio transmission with significant electrical noise...
in transmission channels. Because the check value has a fixed length, the function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
that generates it is occasionally used as a hash function
Hash function
A hash function is any algorithm or subroutine that maps large data sets to smaller data sets, called keys. For example, a single integer can serve as an index to an array...
. The CRC was invented by W. Wesley Peterson
W. Wesley Peterson
William Wesley Peterson was an American mathematician and computer scientist. He was best known for inventing the Cyclic Redundancy Check , for which research he was awarded the Japan Prize in 1999....
in 1961; the 32-bit polynomial used in the CRC function of Ethernet and many other standards is the work of several researchers and was published in 1975.
Introduction
CRCs are based on the theory of cyclic error-correcting codes. The use of systematicSystematic code
In coding theory, a systematic code is any error-correcting code in which the input data is embedded in the encoded output. Conversely, in a non-systematic code the output does not contain the input symbols....
cyclic codes, which encode messages by adding a fixed-length check value, for the purpose of error detection in communication networks was first proposed by W. Wesley Peterson
W. Wesley Peterson
William Wesley Peterson was an American mathematician and computer scientist. He was best known for inventing the Cyclic Redundancy Check , for which research he was awarded the Japan Prize in 1999....
in 1961.
Cyclic codes are not only simple to implement but have the benefit of being particularly well suited for the detection of burst errors, contiguous sequences of erroneous data symbols in messages. This is important because burst errors are common transmission errors in many communication channels, including magnetic and optical storage devices. Typically an n-bit CRC applied to a data block of arbitrary length, will detect any single error burst not longer than n bits and will detect a fraction 1−2−n of all longer error bursts.
Specification of a CRC code requires definition of a so-called generator polynomial. This polynomial resembles the divisor
Divisor
In mathematics, a divisor of an integer n, also called a factor of n, is an integer which divides n without leaving a remainder.-Explanation:...
in a polynomial long division
Polynomial long division
In algebra, polynomial long division is an algorithm for dividing a polynomial by another polynomial of the same or lower degree, a generalised version of the familiar arithmetic technique called long division...
, which takes the message as the dividend
Division (mathematics)
right|thumb|200px|20 \div 4=5In mathematics, especially in elementary arithmetic, division is an arithmetic operation.Specifically, if c times b equals a, written:c \times b = a\,...
and in which the quotient
Quotient
In mathematics, a quotient is the result of division. For example, when dividing 6 by 3, the quotient is 2, while 6 is called the dividend, and 3 the divisor. The quotient further is expressed as the number of times the divisor divides into the dividend e.g. The quotient of 6 and 2 is also 3.A...
is discarded and the remainder
Remainder
In arithmetic, the remainder is the amount "left over" after the division of two integers which cannot be expressed with an integer quotient....
becomes the result, with the important distinction that the polynomial coefficient
Coefficient
In mathematics, a coefficient is a multiplicative factor in some term of an expression ; it is usually a number, but in any case does not involve any variables of the expression...
s are calculated according to the carry-less arithmetic of a finite field
Finite field
In abstract algebra, a finite field or Galois field is a field that contains a finite number of elements. Finite fields are important in number theory, algebraic geometry, Galois theory, cryptography, and coding theory...
. The length of the remainder is always less than the length of the generator polynomial, which therefore determines how long the result can be.
In practice, all commonly used CRCs employ the finite field GF(2)
GF(2)
GF is the Galois field of two elements. It is the smallest finite field.- Definition :The two elements are nearly always called 0 and 1, being the additive and multiplicative identities, respectively...
. This is the field of two elements, usually called 0 and 1, comfortably matching computer architecture. The rest of this article will discuss only these binary CRCs, but the principles are more general.
The simplest error-detection system, the parity bit
Parity bit
A parity bit is a bit that is added to ensure that the number of bits with the value one in a set of bits is even or odd. Parity bits are used as the simplest form of error detecting code....
, is in fact a trivial 1-bit CRC: it uses the generator polynomial x+1.
Application
A CRC-enabled device calculates a short, fixed-length binary sequence, known as the check value or improperly the CRC, for each block of data to be sent or stored and appends it to the data, forming a codeword. When a codeword is received or read, the device either compares its check value with one freshly calculated from the data block, or equivalently, performs a CRC on the whole codeword and compares the resulting check value with an expected residue constant. If the check values do not match, then the block contains a data error and the device may take corrective action such as rereading or requesting the block be sent again, otherwise the data is assumed to be error-free (though, with some small probability, it may contain undetected errors; this is the fundamental nature of error-checking).CRCs and data integrity
CRCs are specifically designed to protect against common types of errors on communication channels, where they can provide quick and reasonable assurance of the integrityData integrity
Data Integrity in its broadest meaning refers to the trustworthiness of system resources over their entire life cycle. In more analytic terms, it is "the representational faithfulness of information to the true state of the object that the information represents, where representational faithfulness...
of messages delivered. However, they are not suitable for protecting against intentional alteration of data. Firstly, as there is no authentication, an attacker can edit a message and recalculate the CRC without the substitution being detected. This is even the case when the CRC is encrypted, leading to one of the design flaws of the WEP
Wired Equivalent Privacy
Wired Equivalent Privacy is a weak security algorithm for IEEE 802.11 wireless networks. Introduced as part of the original 802.11 standard ratified in September 1999, its intention was to provide data confidentiality comparable to that of a traditional wired network...
protocol. Secondly, the linear
Linear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
properties of CRC codes even allow an attacker to modify a message in such a way as to leave the check value unchanged, and otherwise permit efficient recalculation of the CRC for compact changes. Nonetheless, it is still often falsely assumed that when a message and its correct check value are received from an open channel then the message cannot have been altered in transit.
Cryptographic hash function
Cryptographic hash function
A cryptographic hash function is a deterministic procedure that takes an arbitrary block of data and returns a fixed-size bit string, the hash value, such that an accidental or intentional change to the data will change the hash value...
s, while still not providing security against intentional alteration when used in this manner, can provide stronger error checking in that they do not rely on specific error pattern assumptions. However, they are much slower than CRCs, and are therefore commonly used to protect off-line data, such as files on servers or databases.
When stored alongside the data, CRCs and cryptographic hash functions by themselves do not protect against intentional modification of data. Any application that requires protection against such attacks must use cryptographic authentication mechanisms, such as message authentication code
Message authentication code
In cryptography, a message authentication code is a short piece of information used to authenticate a message.A MAC algorithm, sometimes called a keyed hash function, accepts as input a secret key and an arbitrary-length message to be authenticated, and outputs a MAC...
s.
Computation of CRC
To compute an n-bit binary CRC, line the bits representing the input in a row, and position the (n+1)-bit pattern representing the CRC's divisor (called a "polynomialPolynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
") underneath the left-hand end of the row.
Start with the message to be encoded:
11010011101100
This is first padded with zeroes corresponding to the bit length n of the CRC. Here is the first calculation for computing a 3-bit CRC:
11010011101100 000 <--- input left shifted by 3 bits
1011 <--- divisor (4 bits) = x³+x+1
------------------
01100011101100 000 <--- result
If the input bit above the leftmost divisor bit is 0, do nothing. If the input bit above the leftmost divisor bit is 1, the divisor is XORed into the input (in other words, the input bit above each 1-bit in the divisor is toggled). The divisor is then shifted one bit to the right, and the process is repeated until the divisor reaches the right-hand end of the input row. Here is the entire calculation:
11010011101100 000 <--- input left shifted by 3 bits
1011 <--- divisor
01100011101100 000 <--- result
1011 <--- divisor ...
00111011101100 000
1011
00010111101100 000
1011
00000001101100 000
1011
00000000110100 000
1011
00000000011000 000
1011
00000000001110 000
1011
00000000000101 000
101 1
-----------------
00000000000000 100 <---remainder (3 bits)
Since the leftmost divisor bit zeroed every input bit it touched, when this process ends the only bits in the input row that can be nonzero are the n bits at the right-hand end of the row. These n bits are the remainder of the division step, and will also be the value of the CRC function (unless the chosen CRC specification calls for some postprocessing).
The validity of a received message can easily be verified by performing the above calculation again, this time with the check value added instead of zeroes. The remainder should equal zero if there are no detectable errors.
11010011101100 100 <--- input with check value
1011 <--- divisor
01100011101100 100 <--- result
1011 <--- divisor ...
00111011101100 100
......
00000000001110 100
1011
00000000000101 100
101 1
------------------
0 <--- remainder
Mathematics of CRC
Mathematical analysis of this division-like process reveals how to pick a divisor that guarantees good error-detection properties. In this analysis, the digits of the bit strings are thought of as the coefficients of a polynomial in some variable x—coefficients that are elements of the finite field GF(2)GF(2)
GF is the Galois field of two elements. It is the smallest finite field.- Definition :The two elements are nearly always called 0 and 1, being the additive and multiplicative identities, respectively...
instead of more familiar numbers. This binary polynomial is treated as a ring
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
. A ring is, loosely speaking, a set of elements somewhat like numbers, that can be operated on by an operation that somewhat resembles addition and another operation that somewhat resembles multiplication, these operations possessing many of the familiar arithmetic properties of commutativity, associativity, and distributivity. Ring theory is part of abstract algebra
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
.
Designing CRC polynomials
The selection of generator polynomial is the most important part of implementing the CRC algorithm. The polynomial must be chosen to maximize the error detecting capabilities while minimizing overall collision probabilities.The most important attribute of the polynomial is its length (largest degree(exponent) +1 of any one term in the polynomial), because of its direct influence on the length of the computed check value.
The most commonly used polynomial lengths are:
- 9 bits (CRC-8)
- 17 bits (CRC-16)
- 33 bits (CRC-32)
- 65 bits (CRC-64)
The design of the CRC polynomial depends on the maximum total length of the block to be protected (data + CRC bits), the desired error protection features, and the type of resources for implementing the CRC as well as the desired performance. A common misconception is that the "best" CRC polynomials are derived from either an irreducible polynomial
Irreducible polynomial
In mathematics, the adjective irreducible means that an object cannot be expressed as the product of two or more non-trivial factors in a given set. See also factorization....
or an irreducible polynomial times the factor
 , which adds to the code the ability to detect all errors affecting an odd number of bits. In reality, all the factors described above should enter in the selection of the polynomial. However, choosing a non-irreducible polynomial can result in missed errors due to the ring having zero divisor
, which adds to the code the ability to detect all errors affecting an odd number of bits. In reality, all the factors described above should enter in the selection of the polynomial. However, choosing a non-irreducible polynomial can result in missed errors due to the ring having zero divisorZero divisor
In abstract algebra, a nonzero element a of a ring is a left zero divisor if there exists a nonzero b such that ab = 0. Similarly, a nonzero element a of a ring is a right zero divisor if there exists a nonzero c such that ca = 0. An element that is both a left and a right zero divisor is simply...
s.
The advantage of choosing a primitive polynomial
Primitive polynomial
In field theory, a branch of mathematics, a primitive polynomial is the minimal polynomial of a primitive element of the finite extension field GF...
as the generator for a CRC code is that the resulting code has maximal total block length; in here if r is the degree of the primitive generator polynomial then the maximal total blocklength is equal to
 , and the associated code is able to detect any single bit or double errors. If instead, we used as generator polynomial
, and the associated code is able to detect any single bit or double errors. If instead, we used as generator polynomial 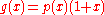 , where
, where 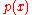 is a primitive polynomial of degree
is a primitive polynomial of degree  , then the maximal total blocklength would be equal to
, then the maximal total blocklength would be equal to 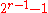 but the code would be able to detect single, double, and triple errors.
but the code would be able to detect single, double, and triple errors.A polynomial
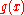 that admits other factorizations may be chosen then so as to balance the maximal total blocklength with a desired error detection power. A powerful class of such polynomials, which subsumes the two examples described above, is that of BCH code
that admits other factorizations may be chosen then so as to balance the maximal total blocklength with a desired error detection power. A powerful class of such polynomials, which subsumes the two examples described above, is that of BCH codeBCH code
In coding theory the BCH codes form a class of parameterised error-correcting codes which have been the subject of much academic attention in the last fifty years. BCH codes were invented in 1959 by Hocquenghem, and independently in 1960 by Bose and Ray-Chaudhuri...
s. Regardless of the reducibility properties of a generator polynomial of degree r, assuming that it includes the "+1" term, such error detection code will be able to detect all error patterns that are confined to a window of r contiguous bits. These patterns are called "error bursts".
Specification of CRC
The concept of the CRC as an error-detecting code gets complicated when an implementer or standards committee turns it into a practical system. Here are some of the complications:- Sometimes an implementation prefixes a fixed bit pattern to the bitstream to be checked. This is useful when clocking errors might insert 0-bits in front of a message, an alteration that would otherwise leave the check value unchanged.
- Sometimes an implementation appends n 0-bits (n being the size of the CRC) to the bitstream to be checked before the polynomial division occurs. This has the convenience that the remainder of the original bitstream with the check value appended is exactly zero, so the CRC can be checked simply by performing the polynomial division on the received bitstream and comparing the remainder with zero.
- Sometimes an implementation exclusive-ORs a fixed bit pattern into the remainder of the polynomial division.
- Bit order: Some schemes view the low-order bit of each byte as "first", which then during polynomial division means "leftmost", which is contrary to our customary understanding of "low-order". This convention makes sense when serial-portSerial portIn computing, a serial port is a serial communication physical interface through which information transfers in or out one bit at a time...
transmissions are CRC-checked in hardware, because some widespread serial-port transmission conventions transmit bytes least-significant bit first. - Byte order: With multi-byte CRCs, there can be confusion over whether the byte transmitted first (or stored in the lowest-addressed byte of memory) is the least-significant byte or the most-significant byte. For example, some 16-bit CRC schemes swap the bytes of the check value.
- Omission of the high-order bit of the divisor polynomial: Since the high-order bit is always 1, and since an n-bit CRC must be defined by an (n+1)-bit divisor which overflowArithmetic overflowThe term arithmetic overflow or simply overflow has the following meanings.# In a computer, the condition that occurs when a calculation produces a result that is greater in magnitude than that which a given register or storage location can store or represent.# In a computer, the amount by which a...
s an n-bit registerProcessor registerIn computer architecture, a processor register is a small amount of storage available as part of a CPU or other digital processor. Such registers are addressed by mechanisms other than main memory and can be accessed more quickly...
, some writers assume that it is unnecessary to mention the divisor's high-order bit. - Omission of the low-order bit of the divisor polynomial: Since the low-order bit is always 1, authors such as Philip Koopman represent polynomials with their high-order bit intact, but without the low-order bit (the
 or 1 term). This convention encodes the polynomial complete with its degree in one integer.
or 1 term). This convention encodes the polynomial complete with its degree in one integer.
These complications mean that there are three common ways to express a polynomial as an integer: the first two, which are mirror images in binary, are the constants found in code; the third is the number found in Koopman's papers. In each case, one term is omitted. So the polynomial
 may be transcribed as:
may be transcribed as:
- 0x3 = 0011b, representing

 (MSB-first code)
(MSB-first code) - 0xC = 1100b, representing

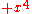
- 0x9 = 1001b, representing


In the table below they are shown as:
| Representations: normal / reversed / reverse of reciprocal |
|---|
| 0x3 / 0xC / 0x9 |
Commonly used and standardized CRCs
Numerous varieties of cyclic redundancy check have been incorporated into technical standards. By no means does one algorithm, or one of each degree, suit every purpose; Koopman and Chakrabarty recommend selecting a polynomial according to the application requirements and the expected distribution of message lengths. The number of distinct CRCs in use have however led to confusion among developers which authors have sought to address. There are three polynomials reported for CRC-12, sixteen conflicting definitions of CRC-16, and six of CRC-32.The polynomials commonly applied are not the most efficient ones possible. Between 1993 and 2004, Koopman, Castagnoli and others surveyed the space of polynomials up to 16 bits, and of 24 and 32 bits, finding examples that have much better performance (in terms of Hamming distance
Hamming distance
In information theory, the Hamming distance between two strings of equal length is the number of positions at which the corresponding symbols are different...
for a given message size) than the polynomials of earlier protocols, and publishing the best of these with the aim of improving the error detection capacity of future standards. In particular, iSCSI
ISCSI
In computing, iSCSI , is an abbreviation of Internet Small Computer System Interface, an Internet Protocol -based storage networking standard for linking data storage facilities. By carrying SCSI commands over IP networks, iSCSI is used to facilitate data transfers over intranets and to manage...
and SCTP have adopted one of the findings of this research, the CRC-32C (Castagnoli) polynomial.
The design of the 32-bit polynomial most commonly used by standards bodies, CRC-32-IEEE, was the result of a joint effort for the Rome Laboratory
Rome Laboratory
The Rome Laboratory, formerly known as the Rome Air Development Center, is one of eight research and development labs run by the US Air Force located at Griffiss AFB in Rome, NY. One of four superlabs run by the Air Force, the Rome Lab is tasked with generic research, as opposed to having a...
and the Air Force Electronic Systems Division by Joseph Hammond, James Brown and Shyan-Shiang Liu of the Georgia Institute of Technology
Georgia Institute of Technology
The Georgia Institute of Technology is a public research university in Atlanta, Georgia, in the United States...
and Kenneth Brayer of the MITRE
MITRE
The Mitre Corporation is a not-for-profit organization based in Bedford, Massachusetts and McLean, Virginia...
Corporation. The earliest known appearances of the 32-bit polynomial were in their 1975 publications: Technical Report 2956 by Brayer for MITRE, published in January and released for public dissemination through DTIC in August, and Hammond, Brown and Liu's report for the Rome Laboratory, published in May. Both reports contained contributions from the other team. In December 1975, Brayer and Hammond presented their work in a paper at the IEEE National Telecommunications Conference: the IEEE CRC-32 polynomial is the generating polynomial of a Hamming code
Hamming code
In telecommunication, Hamming codes are a family of linear error-correcting codes that generalize the Hamming-code invented by Richard Hamming in 1950. Hamming codes can detect up to two and correct up to one bit errors. By contrast, the simple parity code cannot correct errors, and can detect only...
and was selected for its error detection performance. Even so, the Castagnoli CRC-32C polynomial used in iSCSI or SCTP matches its performance on messages from 58 bits–131 kbits, and outperforms it in several size ranges including the two most common sizes of Internet packet. The ITU-T
ITU-T
The ITU Telecommunication Standardization Sector is one of the three sectors of the International Telecommunication Union ; it coordinates standards for telecommunications....
G.hn
G.hn
G.hn is the common name for a home network technology family of standards developed under the International Telecommunication Union's Standardization arm and promoted by the HomeGrid Forum...
standard also uses CRC-32C to detect errors in the payload (although it uses CRC-16-CCITT for PHY headers).
The table below lists only the polynomials of the various algorithms in use. Variations of a particular protocol can impose pre-inversion, post-inversion and reversed bit ordering as described above. For example, the CRC32 used in both Gzip and Bzip2 use the same polynomial, but Bzip2 employs reversed bit ordering, while Gzip does not.
CRCs in proprietary protocols might use a non-trivial initial value and final XOR for obfuscation
Obfuscation
Obfuscation is the hiding of intended meaning in communication, making communication confusing, wilfully ambiguous, and harder to interpret.- Background :Obfuscation may be used for many purposes...
but this does not add cryptographic strength to the algorithm. An unknown error-detecting code can be characterized as a CRC, and as such fully reverse-engineered
Reverse engineering
Reverse engineering is the process of discovering the technological principles of a device, object, or system through analysis of its structure, function, and operation...
, from its output codewords.
| Name | Polynomial | Representations: normal / reversed / reverse of reciprocal |
|---|---|---|
| CRC-1 |  (most hardware; also known as parity bit (most hardware; also known as parity bitParity bit A parity bit is a bit that is added to ensure that the number of bits with the value one in a set of bits is even or odd. Parity bits are used as the simplest form of error detecting code.... ) |
0x1 / 0x1 / 0x1 |
| CRC-4-ITU |  (ITU-T (ITU-TITU-T The ITU Telecommunication Standardization Sector is one of the three sectors of the International Telecommunication Union ; it coordinates standards for telecommunications.... G.704, p. 12) |
0x3 / 0xC / 0x9 |
| CRC-5-EPC |  (Gen 2 RFID) (Gen 2 RFID) |
0x09 / 0x12 / 0x14 |
| CRC-5-ITU |  (ITU-T G.704, p. 9) (ITU-T G.704, p. 9) |
0x15 / 0x15 / 0x1A |
| CRC-5-USB |  (USB (USBUniversal Serial Bus USB is an industry standard developed in the mid-1990s that defines the cables, connectors and protocols used in a bus for connection, communication and power supply between computers and electronic devices.... token packets) |
0x05 / 0x14 / 0x12 |
| CRC-6-ITU |  (ITU-T G.704, p. 3) (ITU-T G.704, p. 3) |
0x03 / 0x30 / 0x21 |
| CRC-7 |  (telecom systems, ITU-T G.707, ITU-T G.832, MMC (telecom systems, ITU-T G.707, ITU-T G.832, MMCMultiMediaCard The MultiMediaCard is a flash memory memory card standard. Unveiled in 1997 by Siemens AG and SanDisk, it is based on Toshiba's NAND-based flash memory, and is therefore much smaller than earlier systems based on Intel NOR-based memory such as CompactFlash. MMC is about the size of a postage... , SD Secure Digital card Secure Digital is a non-volatile memory card format developed by the SD Card Association for use in portable devices. The SD technology is used by more than 400 brands across dozens of product categories and more than 8,000 models, and is considered the de-facto industry standard.Secure Digital... ) |
0x09 / 0x48 / 0x44 |
| CRC-8-CCITT |  (ATM (ATMAsynchronous Transfer Mode Asynchronous Transfer Mode is a standard switching technique designed to unify telecommunication and computer networks. It uses asynchronous time-division multiplexing, and it encodes data into small, fixed-sized cells. This differs from approaches such as the Internet Protocol or Ethernet that... HEC Header Error Correction This is a bit error detection and correction mechanism used in data transmitter and receiver.The Header Error Control is the last field in the Asynchronous Transfer Mode cell consisting of an 8-bit CRC of the cell's header only.... ), ISDN Header Error Control and Cell Delineation ITU-T I.432.1 (02/99) |
0x07 / 0xE0 / 0x83 |
| CRC-8-Dallas Dallas Semiconductor Dallas Semiconductor, now a subsidiary of Maxim Integrated Products, designs and manufactures analog, digital, and mixed-signal semiconductors... /Maxim Maxim Integrated Products Maxim Integrated Products is a publicly traded company that designs, manufactures, and sells analog and mixed-signal semiconductor products. Maxim develops integrated circuits for the industrial, communications, consumer, and computing markets.... |
 (1-Wire (1-Wire1-Wire 1-Wire is a device communications bus system designed by Dallas Semiconductor Corp. that provides low-speed data, signaling, and power over a single signal. 1-Wire is similar in concept to I²C, but with lower data rates and longer range. It is typically used to communicate with small inexpensive... bus) |
0x31 / 0x8C / 0x98 |
| CRC-8 |  |
0xD5 / 0xAB / 0xEA |
| CRC-8-SAE J1850 | 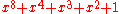 |
0x1D / 0xB8 / 0x8E |
| CRC-8-WCDMA W-CDMA (UMTS) W-CDMA , UMTS-FDD, UTRA-FDD, or IMT-2000 CDMA Direct Spread is an air interface standard found in 3G mobile telecommunications networks. It is the basis of Japan's NTT DoCoMo's FOMA service and the most-commonly used member of the UMTS family and sometimes used as a synonym for UMTS... |
 |
0x9B / 0xD9 / 0xCD |
| CRC-10 |  (ATM; ITU-T I.610) (ATM; ITU-T I.610) |
0x233 / 0x331 / 0x319 |
| CRC-11 |  (FlexRay (FlexRayFlexRay FlexRay is an automotive network communications protocol developed by the . It is designed to be faster and more reliable than CAN and TTP, but is also more expensive... ) |
0x385 / 0x50E / 0x5C2 |
| CRC-12 |  (telecom systems) (telecom systems) |
0x80F / 0xF01 / 0xC07 |
| CRC-15-CAN Controller Area Network Controller–area network is a vehicle bus standard designed to allow microcontrollers and devices to communicate with each other within a vehicle without a host computer.... |
 |
0x4599 / 0x4CD1 / 0x62CC |
| CRC-16-IBM IBM International Business Machines Corporation or IBM is an American multinational technology and consulting corporation headquartered in Armonk, New York, United States. IBM manufactures and sells computer hardware and software, and it offers infrastructure, hosting and consulting services in areas... |
 (Bisync (BisyncBinary Synchronous Communications Binary Synchronous Communication is an IBM link protocol, announced in 1967 after the introduction of System/360. It replaced the synchronous-transmit-receive protocol used with second generation computers. The intent was that common link management rules could be used with three different... , Modbus Modbus Modbus is a serial communications protocol published by Modicon in 1979 for use with its programmable logic controllers . Simple and robust, it has since become one of the de facto standard communications protocols in the industry, and it is now amongst the most commonly available means of... , USB Universal Serial Bus USB is an industry standard developed in the mid-1990s that defines the cables, connectors and protocols used in a bus for connection, communication and power supply between computers and electronic devices.... , ANSI Ansi Ansi is a village in Kaarma Parish, Saare County, on the island of Saaremaa, Estonia.... X3.28, many others; also known as CRC-16 and CRC-16-ANSI) |
0x8005 / 0xA001 / 0xC002 |
| CRC-16-CCITT |  (X.25 (X.25X.25 X.25 is an ITU-T standard protocol suite for packet switched wide area network communication. An X.25 WAN consists of packet-switching exchange nodes as the networking hardware, and leased lines, Plain old telephone service connections or ISDN connections as physical links... , V.41, HDLC, XMODEM XMODEM XMODEM is a simple file transfer protocol developed as a quick hack by Ward Christensen for use in his 1977 MODEM.ASM terminal program. XMODEM became extremely popular in the early bulletin board system market, largely because it was so simple to implement... , Bluetooth Bluetooth Bluetooth is a proprietary open wireless technology standard for exchanging data over short distances from fixed and mobile devices, creating personal area networks with high levels of security... , SD Secure Digital card Secure Digital is a non-volatile memory card format developed by the SD Card Association for use in portable devices. The SD technology is used by more than 400 brands across dozens of product categories and more than 8,000 models, and is considered the de-facto industry standard.Secure Digital... , many others; known as CRC-CCITT) |
0x1021 / 0x8408 / 0x8810 |
| CRC-16-T10-DIF Data Integrity Field DIF stands for Data Integrity Field. The purpose of this field is to provide End-to-End data protection in Computer/Enterprise data storage methodology.... |
 (SCSI (SCSISCSI Small Computer System Interface is a set of standards for physically connecting and transferring data between computers and peripheral devices. The SCSI standards define commands, protocols, and electrical and optical interfaces. SCSI is most commonly used for hard disks and tape drives, but it... DIF) |
0x8BB7 / 0xEDD1 / 0xC5DB |
| CRC-16-DNP DNP3 DNP3 is a set of communications protocols used between components in process automation systems. Its main use is in utilities such as electric and water companies. Usage in other industries is not common. It was developed for communications between various types of data acquisition and control... |
 (DNP, IEC 870 (DNP, IEC 870IEC 60870-5 In electrical engineering and power system automation, the International Electrotechnical Commission 60870 standards define systems used for telecontrol . Such systems are used for controlling electric power transmission grids and other geographically widespread control systems... , M-Bus Meter-Bus M-Bus is a European standard for the remote reading of gas or electricity meters. M-Bus is also usable for other types of consumption meters. The M-Bus interface is made for communication on two wire, making it very cost effective... ) |
0x3D65 / 0xA6BC / 0x9EB2 |
| CRC-16-DECT Digital Enhanced Cordless Telecommunications Digital Enhanced Cordless Telecommunications , usually known by the acronym DECT, is a digital communication standard, which is primarily used for creating cordless phone systems... |
 (cordless telephones) (cordless telephones) |
0x0589 / 0x91A0 / 0x82C4 |
| CRC-16-Fletcher | Not a CRC; see Fletcher's checksum Fletcher's checksum The Fletcher checksum is an algorithm for computing a position-dependent checksum devised by John G. Fletcher at Lawrence Livermore Labs in the late 1970s. A description of the algorithm and an analysis of the performance characteristics of a particular implementation were published in the IEEE... |
Used in Adler-32 Adler-32 Adler-32 is a checksum algorithm which was invented by Mark Adler in 1995, and is a modification of the Fletcher checksum. Compared to a cyclic redundancy check of the same length, it trades reliability for speed. Adler-32 is more reliable than Fletcher-16, and slightly less reliable than Fletcher-32... A & B CRCs |
| CRC-24 |  (FlexRay (FlexRayFlexRay FlexRay is an automotive network communications protocol developed by the . It is designed to be faster and more reliable than CAN and TTP, but is also more expensive... ) |
0x5D6DCB / 0xD3B6BA / 0xAEB6E5 |
| CRC-24-Radix-64 |  (OpenPGP) (OpenPGP) |
0x864CFB / 0xDF3261 / 0xC3267D |
| CRC-30 |  (CDMA) (CDMA) |
0x2030B9C7 / 0x38E74301 / 0x30185CE3 |
| CRC-32-Adler | Not a CRC; see Adler-32 Adler-32 Adler-32 is a checksum algorithm which was invented by Mark Adler in 1995, and is a modification of the Fletcher checksum. Compared to a cyclic redundancy check of the same length, it trades reliability for speed. Adler-32 is more reliable than Fletcher-16, and slightly less reliable than Fletcher-32... |
See Adler-32 Adler-32 Adler-32 is a checksum algorithm which was invented by Mark Adler in 1995, and is a modification of the Fletcher checksum. Compared to a cyclic redundancy check of the same length, it trades reliability for speed. Adler-32 is more reliable than Fletcher-16, and slightly less reliable than Fletcher-32... |
| CRC-32 |  (ISO 3309, ANSI (ISO 3309, ANSIAnsi Ansi is a village in Kaarma Parish, Saare County, on the island of Saaremaa, Estonia.... X3.66, FIPS FIPS - Computer :*FIPS , Fully Interactive Partition Splitter, a disk partitioner*Federal Information Processing Standard, United States government standards*FTC Fair Information Practice, FIPs, US Federal Trade Commission guidelines- People :... PUB 71, FED-STD-1003, ITU-T ITU-T The ITU Telecommunication Standardization Sector is one of the three sectors of the International Telecommunication Union ; it coordinates standards for telecommunications.... V.42, Ethernet Ethernet Ethernet is a family of computer networking technologies for local area networks commercially introduced in 1980. Standardized in IEEE 802.3, Ethernet has largely replaced competing wired LAN technologies.... , SATA Sata Sata is a traditional dish from the Malaysian state of Terengganu, consisting of spiced fish meat wrapped in banana leaves and cooked on a grill.It is a type of Malaysian fish cake, or otak-otak... , MPEG-2 MPEG-2 MPEG-2 is a standard for "the generic coding of moving pictures and associated audio information". It describes a combination of lossy video compression and lossy audio data compression methods which permit storage and transmission of movies using currently available storage media and transmission... , Gzip Gzip Gzip is any of several software applications used for file compression and decompression. The term usually refers to the GNU Project's implementation, "gzip" standing for GNU zip. It is based on the DEFLATE algorithm, which is a combination of Lempel-Ziv and Huffman coding... , PKZIP PKZIP PKZIP is an archiving tool originally written by Phil Katz and marketed by his company PKWARE, Inc. The common "PK" prefix used in both PKZIP and PKWARE stands for "Phil Katz".-History:... , POSIX POSIX POSIX , an acronym for "Portable Operating System Interface", is a family of standards specified by the IEEE for maintaining compatibility between operating systems... cksum Cksum cksum' is a command in Unix-like operating systems that generates a checksum value for a file or stream of data. The cksum command reads each file given in its arguments, or standard input if no arguments are provided, and outputs the file's CRC checksum and byte count.The cksum command can be... , PNG, ZMODEM ZMODEM ZMODEM is a file transfer protocol developed by Chuck Forsberg in 1986, in a project funded by Telenet in order to improve file transfers on their X.25 network... ) |
0x04C11DB7 / 0xEDB88320 / 0x82608EDB |
| (Castagnoli) |  (iSCSI (iSCSIISCSI In computing, iSCSI , is an abbreviation of Internet Small Computer System Interface, an Internet Protocol -based storage networking standard for linking data storage facilities. By carrying SCSI commands over IP networks, iSCSI is used to facilitate data transfers over intranets and to manage... & SCTP, G.hn G.hn G.hn is the common name for a home network technology family of standards developed under the International Telecommunication Union's Standardization arm and promoted by the HomeGrid Forum... payload, SSE4.2) |
0x1EDC6F41 / 0x82F63B78 / 0x8F6E37A0 |
| (Koopman) |  |
0x741B8CD7 / 0xEB31D82E / 0xBA0DC66B |
| CRC-32Q |  (aviation; AIXM (aviation; AIXMAIXM The Aeronautical Information Exchange Model is designed to enable the management and distribution of Aeronautical Information Services data in digital format. AIXM version 5.0, set to be finalized in late 2007, is based on Geography Markup Language and is one of the GML Application Schemas... ) |
0x814141AB / 0xD5828281 / 0xC0A0A0D5 |
| CRC-40-GSM |  (GSM control channel) (GSM control channel) |
0x0004820009 / 0x9000412000 / 0x8002410004 |
| CRC-64-ISO |  (HDLC — ISO 3309 (HDLC — ISO 3309High-Level Data Link Control High-Level Data Link Control is a bit-oriented synchronous data link layer protocol developed by the International Organization for Standardization... , Swiss-Prot/TrEMBL; considered weak for hashing) |
0x000000000000001B / 0xD800000000000000 / 0x800000000000000D |
| CRC-64-ECMA Ecma International Ecma International is an international, private non-profit standards organization for information and communication systems. It acquired its name in 1994, when the European Computer Manufacturers Association changed its name to reflect the organization's global reach and activities... -182 |
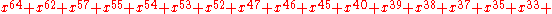  (as described in ECMA-182 p. 51) (as described in ECMA-182 p. 51) |
0x42F0E1EBA9EA3693 / 0xC96C5795D7870F42 / 0xA17870F5D4F51B49 |
See also
- Computation of CRCComputation of CRCComputation of a cyclic redundancy check is derived from the mathematics of polynomial division, modulo two. In practice, it resembles long division of the binary message string, with a fixed number of zeroes appended, by the "generator polynomial" string except that exclusive OR operations replace...
- Error correcting code
- Cyclic code
- Redundancy check
- List of checksum algorithms
- Parity
- Information securityInformation securityInformation security means protecting information and information systems from unauthorized access, use, disclosure, disruption, modification, perusal, inspection, recording or destruction....
- Simple file verification
- cksumCksumcksum' is a command in Unix-like operating systems that generates a checksum value for a file or stream of data. The cksum command reads each file given in its arguments, or standard input if no arguments are provided, and outputs the file's CRC checksum and byte count.The cksum command can be...
- Header Error CorrectionHeader Error CorrectionThis is a bit error detection and correction mechanism used in data transmitter and receiver.The Header Error Control is the last field in the Asynchronous Transfer Mode cell consisting of an 8-bit CRC of the cell's header only....
- Adler-32Adler-32Adler-32 is a checksum algorithm which was invented by Mark Adler in 1995, and is a modification of the Fletcher checksum. Compared to a cyclic redundancy check of the same length, it trades reliability for speed. Adler-32 is more reliable than Fletcher-16, and slightly less reliable than Fletcher-32...
- Fletcher's checksumFletcher's checksumThe Fletcher checksum is an algorithm for computing a position-dependent checksum devised by John G. Fletcher at Lawrence Livermore Labs in the late 1970s. A description of the algorithm and an analysis of the performance characteristics of a particular implementation were published in the IEEE...
- Mathematics of CRCMathematics of CRCThe cyclic redundancy check is based on division in the ring of polynomials over the finite field GF , that is, the set of polynomials where each coefficient is either zero or one, and arithmetic operations wrap around .Any string of bits can be interpreted as the coefficients of a message...
s
External links
- MathPages - Cyclic Redundancy Checks: overview with an explanation of error-detection of different polynomials.
- Clean C++ CRC32 Source Code; OS and Library Independent
- The CRC Pitstop - home of A Painless Guide to CRC Error Detection Algorithms
- Black, R. (1994-02) Fast CRC32 in Software; algorithm 4 is used in Linux and info-zip's zip and unzip.
- Kounavis, M. and Berry, F. (2005). A Systematic Approach to Building High Performance, Software-based, CRC generators, Slicing-by-4 and slicing-by-8 algorithms
- pycrc - a free C/C++ source code generator for various CRC algorithms
- CRC32: Generating a checksum for a file, C++ implementation by Brian Friesen
- The CRC++ Project Implementation in C++ which uses template classes to deal with different bit order
- 'CRC-Analysis with Bitfilters'.
- Cyclic Redundancy Check: theory, practice, hardware, and software with emphasis on CRC-32. A sample chapter from Henry S. Warren, Jr. Hacker's DelightHacker's DelightHacker's Delight by Henry S. Warren, Jr., is a book published by Addison-Wesley Professional July 17, 2002. It discusses a variety of programming algorithms for common tasks involving integer types, often with the aim of performing the minimum number of operations or replacing slow operations by...
. - CRCs Code for CRC-32 and CRC-16 calculation in BASIC, 6502, Z80, PDP-11, 6809, 80x86, ARM and C.
- Reverse-Engineering a CRC Algorithm

