Coupling (probability)
Encyclopedia
In probability theory
, coupling is a proof
technique that allows one to compare two unrelated variables by "forcing" them to be related in some way.
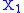and 
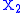be two random variables defined on probability spaces 
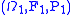and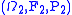 
. Then a coupling of 
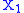and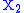 
is a new probability space 
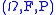over which there are two random variables 
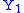and 
such that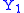 
has the same distribution as 
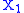while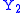 
has the same distribution as 
.
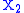The interesting case is when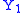
and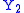 
are not independent.
in two dimensions, but they start from different points. The simplest way to couple them is simply to force them to walk together. On every step, if A walks up, so does B, if A moves to the left, so does B, etc. Thus, the difference between the two particles stays fixed. As far as A is concerned, it is doing a perfect random walk, while B is the copycat. B holds the opposite view, i.e. that he is, in effect, the original and that A is the copy. And in a sense they both are right. In other words, any mathematical theorem, or result that holds for a regular random walk, will also hold for both A and B.
Consider now a more elaborate example. Assume that A starts from the point (0,0) and B from (10,10). First couple them so that they walk together in the vertical direction, i.e. if A goes up, so does B, etc., but are mirror images in the horizontal direction i.e. if A goes left, B goes right and vice versa. We continue this coupling until A and B have the same horizontal coordinate, or in other words are on the vertical line (5,y). If they never meet, we continue this process forever (the probability for that is zero, though). After this event, we change the coupling rule. We let them walk together in the horizontal direction, but in a mirror image rule in the vertical direction. We continue this rule until they meet in the vertical direction too (if they do), and from that point on, we just let them walk together.
This is a coupling in the sense that neither particle, taken on its own, can feel anything we did. Nor that fact that the other particle follows him in one way or the other, nor the fact that we changed the coupling rule or when we did it. Each particle performs a simple random walk. And yet, our coupling rule forces them to meet almost surely
and to continue from that point on together permanently. This allows one to prove many interesting results that say that "in the long run", it is not important where you started.
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
, coupling is a proof
Mathematical proof
In mathematics, a proof is a convincing demonstration that some mathematical statement is necessarily true. Proofs are obtained from deductive reasoning, rather than from inductive or empirical arguments. That is, a proof must demonstrate that a statement is true in all cases, without a single...
technique that allows one to compare two unrelated variables by "forcing" them to be related in some way.
Definition
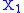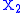Using the standard formalism of probability, let and be two random variables defined on probability spaces 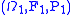and 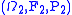. Then a coupling of 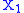and 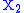is a new probability space 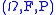over which there are two random variables 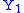and such that 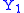has the same distribution as 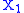while 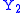has the same distribution as 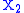.The interesting case is when
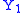and 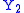are not independent.Examples
Assume two particles A and B perform a simple random walkRandom walk
A random walk, sometimes denoted RW, is a mathematical formalisation of a trajectory that consists of taking successive random steps. For example, the path traced by a molecule as it travels in a liquid or a gas, the search path of a foraging animal, the price of a fluctuating stock and the...
in two dimensions, but they start from different points. The simplest way to couple them is simply to force them to walk together. On every step, if A walks up, so does B, if A moves to the left, so does B, etc. Thus, the difference between the two particles stays fixed. As far as A is concerned, it is doing a perfect random walk, while B is the copycat. B holds the opposite view, i.e. that he is, in effect, the original and that A is the copy. And in a sense they both are right. In other words, any mathematical theorem, or result that holds for a regular random walk, will also hold for both A and B.
Consider now a more elaborate example. Assume that A starts from the point (0,0) and B from (10,10). First couple them so that they walk together in the vertical direction, i.e. if A goes up, so does B, etc., but are mirror images in the horizontal direction i.e. if A goes left, B goes right and vice versa. We continue this coupling until A and B have the same horizontal coordinate, or in other words are on the vertical line (5,y). If they never meet, we continue this process forever (the probability for that is zero, though). After this event, we change the coupling rule. We let them walk together in the horizontal direction, but in a mirror image rule in the vertical direction. We continue this rule until they meet in the vertical direction too (if they do), and from that point on, we just let them walk together.
This is a coupling in the sense that neither particle, taken on its own, can feel anything we did. Nor that fact that the other particle follows him in one way or the other, nor the fact that we changed the coupling rule or when we did it. Each particle performs a simple random walk. And yet, our coupling rule forces them to meet almost surely
Almost surely
In probability theory, one says that an event happens almost surely if it happens with probability one. The concept is analogous to the concept of "almost everywhere" in measure theory...
and to continue from that point on together permanently. This allows one to prove many interesting results that say that "in the long run", it is not important where you started.