Conway's Game of Life
Encyclopedia


Cellular automaton
A cellular automaton is a discrete model studied in computability theory, mathematics, physics, complexity science, theoretical biology and microstructure modeling. It consists of a regular grid of cells, each in one of a finite number of states, such as "On" and "Off"...
devised by the British
United Kingdom
The United Kingdom of Great Britain and Northern IrelandIn the United Kingdom and Dependencies, other languages have been officially recognised as legitimate autochthonous languages under the European Charter for Regional or Minority Languages...
mathematician
Mathematician
A mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....
John Horton Conway
John Horton Conway
John Horton Conway is a prolific mathematician active in the theory of finite groups, knot theory, number theory, combinatorial game theory and coding theory...
in 1970.
The "game" is a zero-player game
Zero-player game
A zero-player game is a game that has no sentient players.In computer games, the term refers to programs that use artificial intelligence rather than human players....
, meaning that its evolution is determined by its initial state, requiring no further input. One interacts with the Game of Life by creating an initial configuration and observing how it evolves.
Rules
The universe of the Game of Life is an infinite two-dimensional orthogonal grid of square cells, each of which is in one of two possible states, alive or dead. Every cell interacts with its eight neighboursMoore neighborhood
In cellular automata, the Moore neighborhood comprises the eight cells surrounding a central cell on a two-dimensional square lattice. The neighborhood is named after Edward F. Moore, a pioneer of cellular automata theory. It is one of the two most commonly used neighborhood types, the other one...
, which are the cells that are horizontally, vertically, or diagonally adjacent. At each step in time, the following transitions occur:
- Any live cell with fewer than two live neighbours dies, as if caused by under-population.
- Any live cell with two or three live neighbours lives on to the next generation.
- Any live cell with more than three live neighbours dies, as if by overcrowding.
- Any dead cell with exactly three live neighbours becomes a live cell, as if by reproduction.
The initial pattern constitutes the seed of the system. The first generation is created by applying the above rules simultaneously to every cell in the seed—births and deaths occur simultaneously, and the discrete moment at which this happens is sometimes called a tick (in other words, each generation is a pure function of the preceding one). The rules continue to be applied repeatedly to create further generations.
Origins
Conway was interested in a problem presented in the 1940s by mathematician John von NeumannJohn von Neumann
John von Neumann was a Hungarian-American mathematician and polymath who made major contributions to a vast number of fields, including set theory, functional analysis, quantum mechanics, ergodic theory, geometry, fluid dynamics, economics and game theory, computer science, numerical analysis,...
, who attempted to find a hypothetical machine that could build copies of itself and succeeded when he found a mathematical model for such a machine with very complicated rules on a rectangular grid. The Game of Life emerged as Conway's successful attempt to drastically simplify von Neumann's ideas.
The game made its first public appearance in the October 1970 issue of Scientific American
Scientific American
Scientific American is a popular science magazine. It is notable for its long history of presenting science monthly to an educated but not necessarily scientific public, through its careful attention to the clarity of its text as well as the quality of its specially commissioned color graphics...
, in Martin Gardner
Martin Gardner
Martin Gardner was an American mathematics and science writer specializing in recreational mathematics, but with interests encompassing micromagic, stage magic, literature , philosophy, scientific skepticism, and religion...
's "Mathematical Games" column. From a theoretical point of view, it is interesting because it has the power of a universal Turing machine
Universal Turing machine
In computer science, a universal Turing machine is a Turing machine that can simulate an arbitrary Turing machine on arbitrary input. The universal machine essentially achieves this by reading both the description of the machine to be simulated as well as the input thereof from its own tape. Alan...
: that is, anything that can be computed algorithm
Algorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
ically can be computed within Conway's Game of Life. Gardner wrote:
The game made Conway instantly famous, but it also opened up a whole new field of mathematical research, the field of cellular automata ... Because of Life's analogies with the rise, fall and alterations of a society of living organisms, it belongs to a growing class of what are called 'simulation games' (games that resemble real life processes)
Ever since its publication, Conway's Game of Life has attracted much interest, because of the surprising ways in which the patterns can evolve. Life provides an example of emergence
Emergence
In philosophy, systems theory, science, and art, emergence is the way complex systems and patterns arise out of a multiplicity of relatively simple interactions. Emergence is central to the theories of integrative levels and of complex systems....
and self-organization
Self-organization
Self-organization is the process where a structure or pattern appears in a system without a central authority or external element imposing it through planning...
. It is interesting for computer scientists
Computer science
Computer science or computing science is the study of the theoretical foundations of information and computation and of practical techniques for their implementation and application in computer systems...
, physicists
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
, biologists
Biology
Biology is a natural science concerned with the study of life and living organisms, including their structure, function, growth, origin, evolution, distribution, and taxonomy. Biology is a vast subject containing many subdivisions, topics, and disciplines...
, biochemists
Biochemistry
Biochemistry, sometimes called biological chemistry, is the study of chemical processes in living organisms, including, but not limited to, living matter. Biochemistry governs all living organisms and living processes...
, economists
Economics
Economics is the social science that analyzes the production, distribution, and consumption of goods and services. The term economics comes from the Ancient Greek from + , hence "rules of the house"...
, mathematicians
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, philosophers
Philosophy
Philosophy is the study of general and fundamental problems, such as those connected with existence, knowledge, values, reason, mind, and language. Philosophy is distinguished from other ways of addressing such problems by its critical, generally systematic approach and its reliance on rational...
, generative scientists
Generative sciences
The generative science is a interdisciplinary and multidisciplinary science that explores the natural world and its complex behaviours as a generative process...
and others to observe the way that complex patterns can emerge from the implementation of very simple rules. The game can also serve as a didactic analogy
Analogy
Analogy is a cognitive process of transferring information or meaning from a particular subject to another particular subject , and a linguistic expression corresponding to such a process...
, used to convey the somewhat counter-intuitive notion that "design" and "organization" can spontaneously emerge in the absence of a designer. For example, philosopher and cognitive scientist Daniel Dennett
Daniel Dennett
Daniel Clement Dennett is an American philosopher, writer and cognitive scientist whose research centers on the philosophy of mind, philosophy of science and philosophy of biology, particularly as those fields relate to evolutionary biology and cognitive science. He is currently the Co-director of...
has used the analogue of Conway's Life "universe" extensively to illustrate the possible evolution of complex philosophical constructs, such as consciousness
Consciousness
Consciousness is a term that refers to the relationship between the mind and the world with which it interacts. It has been defined as: subjectivity, awareness, the ability to experience or to feel, wakefulness, having a sense of selfhood, and the executive control system of the mind...
and free will
Free will
"To make my own decisions whether I am successful or not due to uncontrollable forces" -Troy MorrisonA pragmatic definition of free willFree will is the ability of agents to make choices free from certain kinds of constraints. The existence of free will and its exact nature and definition have long...
, from the relatively simple set of deterministic physical laws governing our own universe.
The popularity of Conway's Game of Life was helped by its coming into being just in time for a new generation of inexpensive minicomputer
Minicomputer
A minicomputer is a class of multi-user computers that lies in the middle range of the computing spectrum, in between the largest multi-user systems and the smallest single-user systems...
s which were being released into the market. The game could be run for hours on these machines, which would otherwise have remained unused at night. In this respect, it foreshadowed the later popularity of computer-generated fractals. For many, Life was simply a programming challenge; a fun way to use otherwise wasted CPU
Central processing unit
The central processing unit is the portion of a computer system that carries out the instructions of a computer program, to perform the basic arithmetical, logical, and input/output operations of the system. The CPU plays a role somewhat analogous to the brain in the computer. The term has been in...
cycles. For some, however, Life had more philosophical connotations. It developed a cult following through the 1970s and beyond; current developments have gone so far as to create theoretic emulations of computer systems within the confines of a Life board.
Conway chose his rules carefully, after considerable experimentation, to meet these criteria:
- There should be no explosive growth, which is why 34 Life was rejected.
- There should exist small initial patterns with chaotic, unpredictable outcomes.
- There should be potential for von Neumann universal constructorVon Neumann universal constructorJohn von Neumann's Universal Constructor is a self-replicating machine in a cellular automata environment. It was designed in the 1940s, without the use of a computer. The fundamental details of the machine were published in von Neumann's book Theory of Self-Reproducing Automata, completed in...
s. - The rules should be as simple as possible, whilst adhering to the above constraints.
Examples of patterns
The earliest interesting patterns in the Game of Life were discovered without the use of computers. The simplest static patterns ("still lifesStill life (CA)
In Conway's Game of Life and other cellular automata, a still life is a pattern that does not change from one generation to the next. A still life can be thought of as an oscillator with unit period.-Pseudo still lifes:...
") and repeating patterns ("oscillators
Oscillator (CA)
In a cellular automaton, an oscillator is a pattern that returns to its original state, in the same orientation and position, after a finite number of generations. Thus the evolution of such a pattern repeats itself indefinitely...
"—a superset of still lifes) were discovered while tracking the fates of various small starting configurations using graph paper, blackboards, physical game boards (such as Go
Go (board game)
Go , is an ancient board game for two players that originated in China more than 2,000 years ago...
) and the like. During this early research, Conway discovered that the F-pentomino
Pentomino
A pentomino is a polyomino composed of five congruent squares, connected along their edges ....
(which he called the "R-pentomino") failed to stabilize in a small number of generations. In fact, it takes 1103 generations to stabilize, by which time it has a population of 116 and has fired six escaping gliders (in fact, these were the first gliders ever discovered).
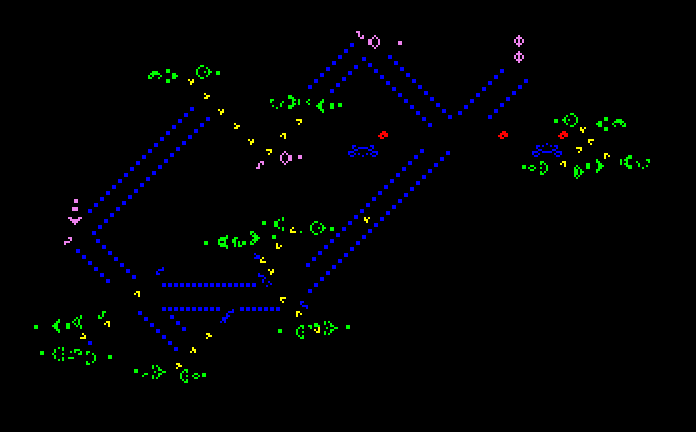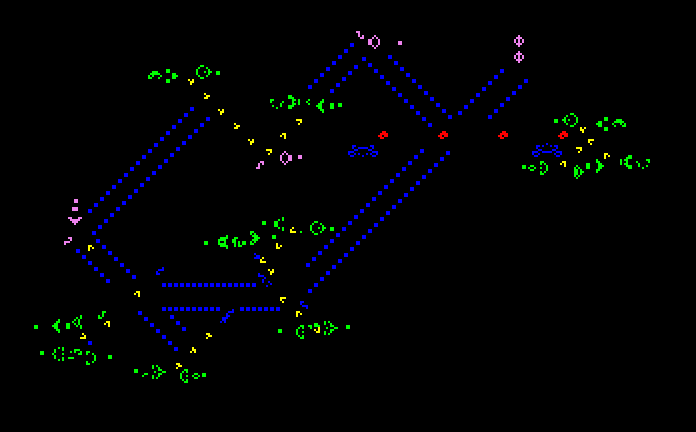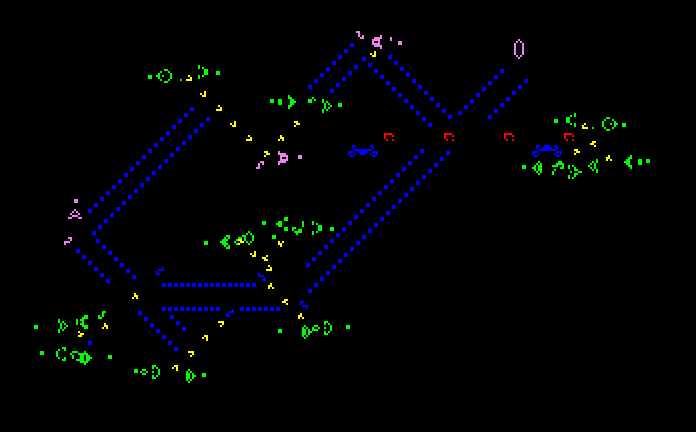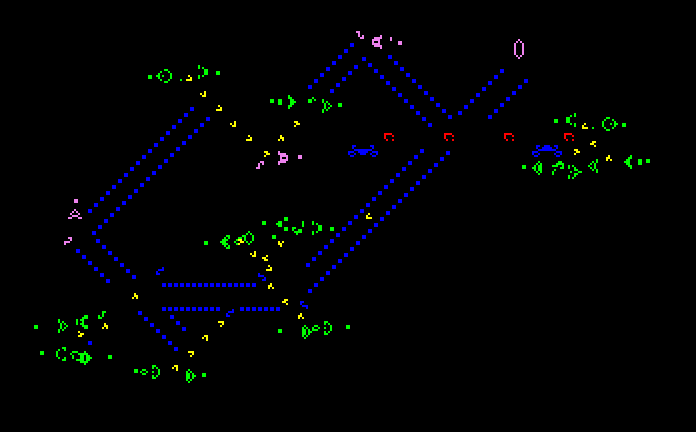
Many different types of patterns occur in the Game of Life, including still lifes, oscillators, and patterns that translate themselves across the board ("spaceships
Spaceship (CA)
In a cellular automaton, a finite pattern is called a spaceship if it reappears after a certain number of generations in the same orientation but in a different position...
"). Some frequently occurring examples of these three classes are shown below, with live cells shown in black, and dead cells shown in white.
|
|
| ||||||||||||||||||||||||||
The "pulsar" is the most common period 3 oscillator. The great majority of naturally occurring oscillators are period 2, like the blinker and the toad, but periods 4, 8, 14, 15, 30 and a few others have been seen on rare occasions.
Patterns called "Methuselahs" can evolve for long periods before stabilizing, the first-discovered of which was the F-pentomino. "Diehard" is a pattern that eventually disappears (rather than merely stabilize) after 130 generations, which is conjectured to be maximal for patterns with seven or fewer cells. "Acorn" takes 5206 generations to generate 633 cells including 13 escaped gliders.
Conway originally conjectured that no pattern can grow indefinitely—i.e., that for any initial configuration with a finite number of living cells, the population cannot grow beyond some finite upper limit. In the game's original appearance in "Mathematical Games", Conway offered a $50 prize to the first person who could prove or disprove the conjecture before the end of 1970. One way to disprove it would be to discover patterns that keep adding counters to the field: a "gun", which would be a configuration that repeatedly shoots out moving objects such as the "glider". Another way of disproving the conjecture would be to construct a "puffer train", which would be a configuration that moves but leaves behind a trail of persistent "smoke".
The prize was won in November of the same year by a team from the Massachusetts Institute of Technology
Massachusetts Institute of Technology
The Massachusetts Institute of Technology is a private research university located in Cambridge, Massachusetts. MIT has five schools and one college, containing a total of 32 academic departments, with a strong emphasis on scientific and technological education and research.Founded in 1861 in...
, led by Bill Gosper
Bill Gosper
Ralph William Gosper, Jr. , known as Bill Gosper, is an American mathematician and programmer from Pennsauken Township, New Jersey...
; the "Gosper glider gun" shown below produces its first glider on the 15th generation, and another glider every 30th generation from then on. This first glider gun is still the smallest one known:
Smaller patterns were later found that also exhibit infinite growth. All three of the following patterns grow indefinitely: the first two create one "block-laying switch engine" each, while the third creates two. The first has only 10 live cells (which has been proven to be minimal). The second fits in a 5 × 5 square. The third is only one cell high:
| |
Later discoveries included other "guns
Gun (CA)
In a cellular automaton, a gun is a pattern with a main part that repeats periodically, like an oscillator, and that also periodically emits spaceships. There are then two periods that may be considered: the period of the spaceship output, and the period of the gun itself, which is necessarily a...
", which are stationary, and which shoot out gliders or other spaceships; "puffers
Puffer train (CA)
In a cellular automaton a puffer train, or simply puffer, is a finite pattern that moves itself across the "universe", leaving debris behind. Thus a pattern consisting of only a puffer will grow arbitrarily large over time. Puffers differ from spaceships in that spaceships do not leave debris behind...
", which move along leaving behind a trail of debris; and "rakes
Rake (CA)
A rake in a cellular automaton is a puffer that, instead of leaving behind a trail of debris, emits a stream of spaceships. In Conway's Game of Life, the discovery of rakes was one of the key components needed to form the breeder, the first known patterns in Life in which the number of live cells...
", which move and emit spaceships. Gosper also constructed the first pattern with an asymptotically optimal
Asymptotically optimal
In computer science, an algorithm is said to be asymptotically optimal if, roughly speaking, for large inputs it performs at worst a constant factor worse than the best possible algorithm...
quadratic growth rate
Quadratic growth
In mathematics, a function or sequence is said to exhibit quadratic growth when its values are proportional to the square of the function argument or sequence position, in the limit as the argument or sequence position goes to infinity...
, called a "breeder", or "lobster", which worked by leaving behind a trail of guns.
It is possible for gliders to interact with other objects in interesting ways. For example, if two gliders are shot at a block in just the right way, the block will move closer to the source of the gliders. If three gliders are shot in just the right way, the block will move farther away. This "sliding block memory" can be used to simulate a counter
Counter
In digital logic and computing, a counter is a device which stores the number of times a particular event or process has occurred, often in relationship to a clock signal.- Electronic counters :...
. It is possible to construct logic gate
Logic gate
A logic gate is an idealized or physical device implementing a Boolean function, that is, it performs a logical operation on one or more logic inputs and produces a single logic output. Depending on the context, the term may refer to an ideal logic gate, one that has for instance zero rise time and...
s such as AND
Logical conjunction
In logic and mathematics, a two-place logical operator and, also known as logical conjunction, results in true if both of its operands are true, otherwise the value of false....
, OR
Logical disjunction
In logic and mathematics, a two-place logical connective or, is a logical disjunction, also known as inclusive disjunction or alternation, that results in true whenever one or more of its operands are true. E.g. in this context, "A or B" is true if A is true, or if B is true, or if both A and B are...
and NOT
Negation
In logic and mathematics, negation, also called logical complement, is an operation on propositions, truth values, or semantic values more generally. Intuitively, the negation of a proposition is true when that proposition is false, and vice versa. In classical logic negation is normally identified...
using gliders. It is possible to build a pattern that acts like a finite state machine
Finite state machine
A finite-state machine or finite-state automaton , or simply a state machine, is a mathematical model used to design computer programs and digital logic circuits. It is conceived as an abstract machine that can be in one of a finite number of states...
connected to two counters. This has the same computational power as a universal Turing machine
Universal Turing machine
In computer science, a universal Turing machine is a Turing machine that can simulate an arbitrary Turing machine on arbitrary input. The universal machine essentially achieves this by reading both the description of the machine to be simulated as well as the input thereof from its own tape. Alan...
, so the Game of Life is theoretically as powerful as any computer with unlimited memory and no time constraints: it is Turing complete.
Furthermore, a pattern can contain a collection of guns that fire gliders in such a way as to construct new objects, including copies of the original pattern. A "universal constructor" can be built which contains a Turing complete computer, and which can build many types of complex objects, including more copies of itself.
Self-replication
On May 18, 2010, Andrew J. Wade announced a self-constructing pattern dubbed Gemini which creates a copy of itself while destroying its parent. This pattern replicates in 34 million generations, and uses an instruction tape made of gliders which oscillate between two stable configurations made of Chapman-Greene construction arms. These, in turn, create new copies of the pattern, and destroy the previous copy. Gemini is a spaceship.Iteration
From a random initial pattern of living cells on the grid, observers will find the population constantly changing as the generations tick by. The patterns that emerge from the simple rules may be considered a form of beautyMathematical beauty
Many mathematicians derive aesthetic pleasure from their work, and from mathematics in general. They express this pleasure by describing mathematics as beautiful. Sometimes mathematicians describe mathematics as an art form or, at a minimum, as a creative activity...
. Small isolated subpatterns with no initial symmetry tend to become symmetrical. Once this happens, the symmetry may increase in richness, but it cannot be lost unless a nearby subpattern comes close enough to disturb it. In a very few cases the society eventually dies out, with all living cells vanishing, though this may not happen for a great many generations. Most initial patterns eventually "burn out", producing either stable figures or patterns that oscillate forever between two or more states; many also produce one or more gliders or spaceships that travel indefinitely away from the initial location. Spaceships can travel
at most one cell per unit time: so this velocity is set to be the cellular automaton speed of light
Speed of light (cellular automaton)
In Conway's Game of Life , the speed of light is a propagation rate across the grid of exactly one step per generation...
and denoted
 .
.Algorithms
Early patterns with unknown futures, such as the R-pentomino, led computer programmers across the world to write programs to track the evolution of Life patterns. Most of the early algorithms were similar; they represented Life patterns as two-dimensional arrays in computer memory. Typically two arrays are used, one to hold the current generation, and one in which to calculate its successor. Often 0 and 1 represent dead and live cells respectively. A nested for-loop considers each element of the current array in turn, counting the live neighbours of each cell to decide whether the corresponding element of the successor array should be 0 or 1. The successor array is displayed. For the next iteration the arrays swap roles so that the successor array in the last iteration becomes the current array in the next iteration.A variety of minor enhancements to this basic scheme are possible, and there are many ways to save unnecessary computation. A cell that did not change at the last time step, and none of whose neighbours changed, is guaranteed not to change at the current time step as well. So, a program that keeps track of which areas are active can save time by not updating the inactive zones.
In principle, the Life field is infinite, but computers have finite memory, and array sizes must usually be declared in advance. This leads to problems when the active area encroaches on the border of the array. Programmers have used several strategies to address these problems. The simplest strategy is simply to assume that every cell outside the array is dead. This is easy to program, but leads to inaccurate results when the active area crosses the boundary. A more sophisticated trick is to consider the left and right edges of the field to be stitched together, and the top and bottom edges also, yielding a toroidal
Torus
In geometry, a torus is a surface of revolution generated by revolving a circle in three dimensional space about an axis coplanar with the circle...
array. The result is that active areas that move across a field edge reappear at the opposite edge. Inaccuracy can still result if the pattern grows too large, but at least there are no pathological edge effects. Techniques of dynamic storage allocation may also be used, creating ever-larger arrays to hold growing patterns.
Alternatively, the programmer may abandon the notion of representing the Life field with a 2-dimensional array, and use a different data structure, like a vector of coordinate pairs representing live cells. This approach allows the pattern to move about the field unhindered, as long as the population does not exceed the size of the live-coordinate array. The drawback is that counting live neighbours becomes a search operation, slowing down simulation speed. With more sophisticated data structures this problem can also be largely solved.
For exploring large patterns at great time-depths, sophisticated algorithms such as Hashlife
Hashlife
Hashlife is a memoized algorithm for computing the long-term fate of a given starting configuration in Conway's Game of Life and related cellular automata, much more quickly than would be possible using alternative algorithms that simulate each time step of each cell of the automaton...
may be useful. There is also a method, applicable to other cellular automata too, for implementation of the Game of Life using arbitrary asynchronous updates whilst still exactly emulating the behaviour of the synchronous game.
Variations on Life
Since Life's inception, new similar cellular automata have been developed. The standard Game of Life, in which a cell is "born" if it has exactly 3 neighbours, stays alive if it has 2 or 3 living neighbours, and dies otherwise, is symbolised as "B3/S23". The first number, or list of numbers, is what is required for a dead cell to be born. The second set is the requirement for a live cell to survive to the next generation. Hence "B6/S16" means "a cell is born if there are 6 neighbours, and lives on if there are either 1 or 6 neighbours". Cellular automata on a two-dimensional grid that can be described in this way are known as Life-like cellular automata. Another common Life-like automaton, HighLifeHighLife
HighLife is a cellular automaton similar to Conway's Game of Life. It was devised in 1994 by Nathan Thompson. It is a two-dimensional, two-state cellular automaton in the "Life family" and is described by the rule B36/S23; that is, a cell is born if it has 3 or 6 neighbors and survives if it has 2...
, is described by the rule B36/S23, because having 6 neighbours, in addition to the original game's B3/S23 rule, causes a birth. HighLife is best known for its frequently occurring replicators. Additional Life-like cellular automata exist, although the vast majority of them produce universes that are either too chaotic or too desolate to be of interest.
Elementary cellular automaton
In mathematics and computability theory, an elementary cellular automaton is a one-dimensional cellular automaton where there are two possible states and the rule to determine the state of a cell in the next generation depends only on the current state of the cell and its two immediate neighbors....
) and 3-D square variations have been developed, as have 2-D hexagonal and 2-D triangular variations.
Conway's rules may also be generalized such that instead of two states (live and dead) there are three or more. State transitions are then determined either by a weighting system or by a table specifying separate transition rules for each state; for example, Mirek's Cellebration
Mirek's Cellebration
Mirek's Cellebration is a 32-bit Windows freeware program designed by Polish computer programmer Mirek Wójtowicz for running one-dimensional and two-dimensional cellular automata ....
's multi-coloured "Rules Table" and "Weighted Life" rule families each include sample rules equivalent to Conway's Life.
Patterns relating to fractals and fractal systems may also be observed in certain Life-like variations. For example, the automaton B1/S12 generates four very close approximations to the Sierpiński triangle
Sierpinski triangle
The Sierpinski triangle , also called the Sierpinski gasket or the Sierpinski Sieve, is a fractal and attractive fixed set named after the Polish mathematician Wacław Sierpiński who described it in 1915. However, similar patterns appear already in the 13th-century Cosmati mosaics in the cathedral...
when applied to a single live cell. The Sierpiński triangle can also be observed in Conway's Game of Life by examining the long-term growth of a long single-cell-thick line of live cells, as well as in HighLife
HighLife
HighLife is a cellular automaton similar to Conway's Game of Life. It was devised in 1994 by Nathan Thompson. It is a two-dimensional, two-state cellular automaton in the "Life family" and is described by the rule B36/S23; that is, a cell is born if it has 3 or 6 neighbors and survives if it has 2...
, Seeds (B2/S), and Wolfram's Rule 90
Rule 90
Rule 90 is an elementary cellular automaton based on the exclusive or function. It consists of a one-dimensional array of cells, each of which can hold either a 0 or a 1 value; in each time step all values are simultaneously replaced by the exclusive or of the two neighboring values...
.
Immigration is a variation that is very similar to Conway's Game of Life, except that there are two ON states (often expressed as two different colours). Whenever a new cell is born, it takes on the ON state that is the majority in the three cells that gave it birth. This feature can be used to examine interactions between spaceships
Spaceship (CA)
In a cellular automaton, a finite pattern is called a spaceship if it reappears after a certain number of generations in the same orientation but in a different position...
and other "objects" within the game. Another similar variation, called QuadLife, involves four different ON states. When a new cell is born from three different ON neighbours, it takes on the fourth value, and otherwise, like Immigration, it takes the majority value. Except for the variation among ON cells, both of these variations act identically to Life.
Video Games
Some games for entertainment purposes have been developed from the Game of Life. One such game, for two players who each interact with the "game" once per tick, is based directly upon Conway's Game of Life. Live cells have one of two colours, and a player wins when all cells of the opponent's colour are eliminated. When a dead cell has three live neighbours, it becomes live in the same colour as the majority of its neighbours, as in the aforementioned Immigration. The game starts with a random or pre-chosen starting pattern with half the live cells of each colour. After one iteration, the first player may add one cell of his or her own colour and remove one cell of his or her opponent's colour. After the next iteration, the other player can do the same, and so forth. Other two-player variants of the Game of Life have also been developed.In Populous II
Populous II
Populous II: Trials of the Olympian Gods is a computer game in the Populous series for the Amiga, Atari ST and DOS-based computers, developed by Bullfrog Productions....
, one of the 'divine intervention' effects is a fungus that grows according to the rules of the Game of Life.
Music
Various musical composition techniques use Conway's Game of Life, especially in MIDI sequencing. A variety of programs exist for creating sound from patterns generated in the Game of Life. (see footnotes for links to examples.)The Native Instruments
Native Instruments
Native Instruments is a technology company that develops software and hardware for music production and DJing. The company has originally been identified mostly with software instruments, but has also expanded to various other music equipment segments in recent years.Current products of Native...
modular sound generation/processing software package Reaktor
Reaktor
Reaktor is a graphical modular software music studio of proprietary license developed by Native Instruments. It lets musicians and sound specialists design and build their own instruments, samplers, effects and sound design tools. It is supplied with many ready-to-use instruments and effects, from...
features a drum machine
Drum machine
A drum machine is an electronic musical instrument designed to imitate the sound of drums or other percussion instruments. They are used in a variety of musical genres, not just purely electronic music...
with an integrated sequencer which implements the Game of Life.
Notable Life programs

The first interactive Life program was written in ALGOL 68
ALGOL 68
ALGOL 68 isan imperative computerprogramming language that was conceived as a successor to theALGOL 60 programming language, designed with the goal of a...
for the PDP-7
PDP-7
The DEC PDP-7 is a minicomputer produced by Digital Equipment Corporation. Introduced in 1965, it was the first to use their Flip-Chip technology. With a cost of only $72,000 USD, it was cheap but powerful by the standards of the time. The PDP-7 was the third of Digital's 18-bit machines, with...
by M. J. T. Guy and S. R. Bourne
Stephen R. Bourne
Steve Bourne is a computer scientist, originally from the United Kingdom and based in the US for most of his career. He is most famous as the author of the Bourne shell , which is the foundation for the standard command line interfaces to Unix....
. Without its help, some discoveries about the game would have been difficult to make. The results were published in the October 1970 issue of Scientific American
Scientific American
Scientific American is a popular science magazine. It is notable for its long history of presenting science monthly to an educated but not necessarily scientific public, through its careful attention to the clarity of its text as well as the quality of its specially commissioned color graphics...
.
There are now thousands of Life programs on line, so a full list will not be provided here. The following is a selection of a small number of programs with some special claim to notability, such as popularity or unusual features. Most of these programs incorporate a graphical user interface for pattern editing and simulation, the capability for simulating multiple rules including Life, and a large library of interesting patterns in Life and other CA rules.
- Conway's Game of Life, by Alan Hensel. A pop-up Java web applet with fast simulation algorithms and a large library of interesting Life patterns.
- Golly. A cross-platform (Windows, Macintosh and Linux) open-source simulation system for Life and other cellular automata, by Andrew Trevorrow and Tomas Rokicki. It includes the hashlifeHashlifeHashlife is a memoized algorithm for computing the long-term fate of a given starting configuration in Conway's Game of Life and related cellular automata, much more quickly than would be possible using alternative algorithms that simulate each time step of each cell of the automaton...
algorithm for extremely fast generation, and PerlPerlPerl is a high-level, general-purpose, interpreted, dynamic programming language. Perl was originally developed by Larry Wall in 1987 as a general-purpose Unix scripting language to make report processing easier. Since then, it has undergone many changes and revisions and become widely popular...
or PythonPython (programming language)Python is a general-purpose, high-level programming language whose design philosophy emphasizes code readability. Python claims to "[combine] remarkable power with very clear syntax", and its standard library is large and comprehensive...
scriptability for both editing and simulation. - Life32. Freeware for Windows machines, it includes powerful and scriptable pattern editing features.
- Mirek's Cellebration. Free 1-D and 2-D cellular automata viewer, explorer and editor for Windows. Includes powerful facilities for simulating and viewing a wide variety of CA rules including Life, and a scriptable editor.
- Xlife. A cellular-automaton laboratory by Jon Bennett. The standard Linux Life simulation application for a long time, it has also been ported to Windows. Can handle cellular automaton rules with the same neighbourhood as Life, and up to eight possible states per cell.
See also
- Hacker EmblemHacker EmblemThe Hacker Emblem was first proposed in October 2003 by Eric S. Raymond, who claimed a need for a unifying and recognizable symbol for his perception of hacker culture...
, depicting a glider - Life-like cellular automatonLife-like cellular automatonA cellular automaton is Life-like if it meets the following criteria:* The array of cells of the automaton has two dimensions....
- Artificial lifeArtificial lifeArtificial life is a field of study and an associated art form which examine systems related to life, its processes, and its evolution through simulations using computer models, robotics, and biochemistry. The discipline was named by Christopher Langton, an American computer scientist, in 1986...
- Langton's antLangton's antLangton's ant is a two-dimensional Turing machine with a very simple set of rules but complicated emergent behavior. It was invented by Chris Langton in 1986 and runs on a square lattice of black and white cells. The universality of Langton's ant was proven in 2000...
, another rule-set that uses a rectangular grid and shows emergent patterns






