Convolution power
Encyclopedia
In mathematics
, the convolution power is the n-fold iteration of the convolution
with itself. Thus if
is a function
on Euclidean space
Rd and
is a natural number
, then the convolution power is defined by
where * denotes the convolution operation of functions on Rd and δ0 is the Dirac delta distribution. This definition makes sense if x is an integrable function (in L1
), a compactly supported distribution
, or is a finite Borel measure.
If x is the distribution function of a random variable
on the real line, then the nth convolution power of x gives the distribution function of the sum of n independent random variables with identical distribution x. The central limit theorem
states that if x is in L1 and L2 with mean zero and variance σ2, then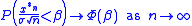
where Φ is the cumulative standard normal distribution on the real line. Equivalently,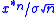
tends weakly to the standard normal distribution.
In some cases, it is possible to define powers x*t for arbitrary real t > 0. If μ is a probability measure
, then μ is infinitely divisible
provided there exists, for each positive integer n, a probability measure μ1/n such that
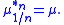
That is, a measure is infinitely divisible if it is possible to define all nth roots. Not every probability measure is infinitely divisible, and a characterization of infinitely divisible measures is of central importance in the abstract theory of stochastic process
es. Intuitively, a measure should be infinitely divisible provided it has a well-defined "convolution logarithm." The natural candidate for measures having such a logarithm are those of (generalized) Poisson
type, given in the form
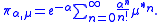
In fact, the Lévy–Khinchin theorem states that a necessary and sufficient condition for a measure to be infinitely divisible is that it must lie in the closure, with respect to the vague topology
, of the class of Poisson measures .
Many applications of the convolution power rely on being able to define the analog of analytic function
s as formal power series
with powers replaced instead by the convolution power. Thus if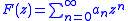
is an analytic function, then one would like to be able to define
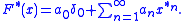
If x ∈ L1(Rd) or more generally is a finite Borel measure on Rd, then the latter series converges absolutely in norm provided that the norm of x is less than the radius of convergence of the original series defining F(z). In particular, it is possible for such measures to define the complex exponential
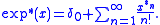
It is not generally possible to extend this definition to arbitrary distributions, although a class of distributions on which this series still converges in an appropriate weak sense is identified by .
As convolution algebras are special cases of Hopf algebra
s, the convolution power is a special case of the (ordinary) power in a Hopf algebra. In applications to quantum field theory
, the convolution exponential, convolution logarithm, and other analytic functions based on the convolution are constructed as formal power series in the elements of the algebra . If, in addition, the algebra is a Banach algebra
, then convergence of the series can be determined as above. In the formal setting, familiar identities such as
continue to hold. Moreover, by the permanence of functional relations, they hold at the level of functions, provided all expressions are well-defined in an open set by convergent series.
where
denotes the derivative
operator. Specifically, this holds if x is a compactly supported distribution or lies in the Sobolev space
W1,1 to ensure that the derivative is sufficiently regular for the convolution to be well-defined.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the convolution power is the n-fold iteration of the convolution
Convolution
In mathematics and, in particular, functional analysis, convolution is a mathematical operation on two functions f and g, producing a third function that is typically viewed as a modified version of one of the original functions. Convolution is similar to cross-correlation...
with itself. Thus if
is a functionFunction (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
on Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
Rd and
is a natural numberNatural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
, then the convolution power is defined by
where * denotes the convolution operation of functions on Rd and δ0 is the Dirac delta distribution. This definition makes sense if x is an integrable function (in L1
Lp space
In mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces...
), a compactly supported distribution
Distribution (mathematics)
In mathematical analysis, distributions are objects that generalize functions. Distributions make it possible to differentiate functions whose derivatives do not exist in the classical sense. In particular, any locally integrable function has a distributional derivative...
, or is a finite Borel measure.
If x is the distribution function of a random variable
Random variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
on the real line, then the nth convolution power of x gives the distribution function of the sum of n independent random variables with identical distribution x. The central limit theorem
Central limit theorem
In probability theory, the central limit theorem states conditions under which the mean of a sufficiently large number of independent random variables, each with finite mean and variance, will be approximately normally distributed. The central limit theorem has a number of variants. In its common...
states that if x is in L1 and L2 with mean zero and variance σ2, then
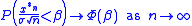
where Φ is the cumulative standard normal distribution on the real line. Equivalently,
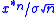tends weakly to the standard normal distribution.In some cases, it is possible to define powers x*t for arbitrary real t > 0. If μ is a probability measure
Probability measure
In mathematics, a probability measure is a real-valued function defined on a set of events in a probability space that satisfies measure properties such as countable additivity...
, then μ is infinitely divisible
Infinite divisibility (probability)
The concepts of infinite divisibility and the decomposition of distributions arise in probability and statistics in relation to seeking families of probability distributions that might be a natural choice in certain applications, in the same way that the normal distribution is...
provided there exists, for each positive integer n, a probability measure μ1/n such that
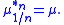
That is, a measure is infinitely divisible if it is possible to define all nth roots. Not every probability measure is infinitely divisible, and a characterization of infinitely divisible measures is of central importance in the abstract theory of stochastic process
Stochastic process
In probability theory, a stochastic process , or sometimes random process, is the counterpart to a deterministic process...
es. Intuitively, a measure should be infinitely divisible provided it has a well-defined "convolution logarithm." The natural candidate for measures having such a logarithm are those of (generalized) Poisson
Poisson process
A Poisson process, named after the French mathematician Siméon-Denis Poisson , is a stochastic process in which events occur continuously and independently of one another...
type, given in the form
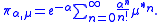
In fact, the Lévy–Khinchin theorem states that a necessary and sufficient condition for a measure to be infinitely divisible is that it must lie in the closure, with respect to the vague topology
Vague topology
In mathematics, particularly in the area of functional analysis and topological vector spaces, the vague topology is an example of the weak-* topology which arises in the study of measures on locally compact Hausdorff spaces....
, of the class of Poisson measures .
Many applications of the convolution power rely on being able to define the analog of analytic function
Analytic function
In mathematics, an analytic function is a function that is locally given by a convergent power series. There exist both real analytic functions and complex analytic functions, categories that are similar in some ways, but different in others...
s as formal power series
Formal power series
In mathematics, formal power series are a generalization of polynomials as formal objects, where the number of terms is allowed to be infinite; this implies giving up the possibility to substitute arbitrary values for indeterminates...
with powers replaced instead by the convolution power. Thus if
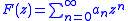is an analytic function, then one would like to be able to define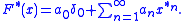If x ∈ L1(Rd) or more generally is a finite Borel measure on Rd, then the latter series converges absolutely in norm provided that the norm of x is less than the radius of convergence of the original series defining F(z). In particular, it is possible for such measures to define the complex exponential
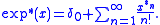
It is not generally possible to extend this definition to arbitrary distributions, although a class of distributions on which this series still converges in an appropriate weak sense is identified by .
As convolution algebras are special cases of Hopf algebra
Hopf algebra
In mathematics, a Hopf algebra, named after Heinz Hopf, is a structure that is simultaneously an algebra and a coalgebra, with these structures' compatibility making it a bialgebra, and that moreover is equipped with an antiautomorphism satisfying a certain property.Hopf algebras occur naturally...
s, the convolution power is a special case of the (ordinary) power in a Hopf algebra. In applications to quantum field theory
Quantum field theory
Quantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
, the convolution exponential, convolution logarithm, and other analytic functions based on the convolution are constructed as formal power series in the elements of the algebra . If, in addition, the algebra is a Banach algebra
Banach algebra
In mathematics, especially functional analysis, a Banach algebra, named after Stefan Banach, is an associative algebra A over the real or complex numbers which at the same time is also a Banach space...
, then convergence of the series can be determined as above. In the formal setting, familiar identities such as
continue to hold. Moreover, by the permanence of functional relations, they hold at the level of functions, provided all expressions are well-defined in an open set by convergent series.
Properties
If x is itself suitably differentiable, then the properties of convolution, one haswhere
denotes the derivativeDerivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
operator. Specifically, this holds if x is a compactly supported distribution or lies in the Sobolev space
Sobolev space
In mathematics, a Sobolev space is a vector space of functions equipped with a norm that is a combination of Lp-norms of the function itself as well as its derivatives up to a given order. The derivatives are understood in a suitable weak sense to make the space complete, thus a Banach space...
W1,1 to ensure that the derivative is sufficiently regular for the convolution to be well-defined.