
Context-free language
Encyclopedia
In formal language theory, a context-free language is a language
generated by some context-free grammar
. The set of all context-free languages is identical to the set of languages accepted by pushdown automata
.
 , the language of all non-empty even-length strings, the entire first halves of which are
, the language of all non-empty even-length strings, the entire first halves of which are  's, and the entire second halves of which are
's, and the entire second halves of which are 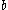 's.
's.  is generated by the grammar
is generated by the grammar 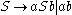 , and is accepted by the pushdown automaton
, and is accepted by the pushdown automaton  where
where 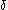 is defined as follows:
is defined as follows:
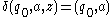
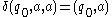
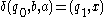
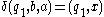
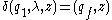
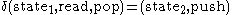
where is initial stack symbol and
is initial stack symbol and  means pop action.
means pop action.
Context-free languages have many applications in programming languages; for example, the language of all properly matched parentheses
is generated by the grammar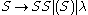 . Also, most arithmetic expressions are generated by context-free grammars.
. Also, most arithmetic expressions are generated by context-free grammars.
under the following operations. That is, if L and P are context-free languages, the following languages are context-free as well:
Context-free languages are not closed under complement
, intersection
, or difference. However, if L is a context-free language and D is a regular language then both their intersection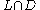 and their difference
and their difference 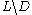 are context-free languages.
are context-free languages.
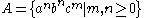 and
and 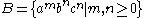 , which are both context-free. Their intersection is
, which are both context-free. Their intersection is 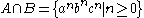 , which can be shown to be non-context-free by the pumping lemma for context-free languages
, which can be shown to be non-context-free by the pumping lemma for context-free languages
.
Context-free languages are also not closed under complementation, as for any languages A and B: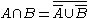 .
.
s A and B:
The following problems are decidable for arbitrary context-free languages:
Formal language
A formal language is a set of words—that is, finite strings of letters, symbols, or tokens that are defined in the language. The set from which these letters are taken is the alphabet over which the language is defined. A formal language is often defined by means of a formal grammar...
generated by some context-free grammar
Context-free grammar
In formal language theory, a context-free grammar is a formal grammar in which every production rule is of the formwhere V is a single nonterminal symbol, and w is a string of terminals and/or nonterminals ....
. The set of all context-free languages is identical to the set of languages accepted by pushdown automata
Pushdown automaton
In automata theory, a pushdown automaton is a finite automaton that can make use of a stack containing data.- Operation :Pushdown automata differ from finite state machines in two ways:...
.
Examples
An archetypical context-free language is , the language of all non-empty even-length strings, the entire first halves of which are
, the language of all non-empty even-length strings, the entire first halves of which are  's, and the entire second halves of which are
's, and the entire second halves of which are 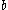 's.
's.  is generated by the grammar
is generated by the grammar 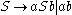 , and is accepted by the pushdown automaton
, and is accepted by the pushdown automaton  where
where 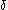 is defined as follows:
is defined as follows: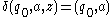
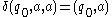
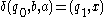
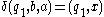
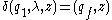
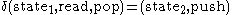
where
 is initial stack symbol and
is initial stack symbol and  means pop action.
means pop action.Context-free languages have many applications in programming languages; for example, the language of all properly matched parentheses
Dyck language
In the theory of formal languages of computer science, mathematics, and linguistics, the Dyck language is the language consisting of balanced strings of parentheses [ and ]. It is important in the parsing of expressions that must have a correctly nested sequence of parentheses, such as arithmetic...
is generated by the grammar
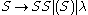 . Also, most arithmetic expressions are generated by context-free grammars.
. Also, most arithmetic expressions are generated by context-free grammars.Closure properties
Context-free languages are closedClosure (mathematics)
In mathematics, a set is said to be closed under some operation if performance of that operation on members of the set always produces a unique member of the same set. For example, the real numbers are closed under subtraction, but the natural numbers are not: 3 and 8 are both natural numbers, but...
under the following operations. That is, if L and P are context-free languages, the following languages are context-free as well:
- the unionUnion (set theory)In set theory, the union of a collection of sets is the set of all distinct elements in the collection. The union of a collection of sets S_1, S_2, S_3, \dots , S_n\,\! gives a set S_1 \cup S_2 \cup S_3 \cup \dots \cup S_n.- Definition :...
 of L and P
of L and P - the reversal of L
- the concatenationConcatenationIn computer programming, string concatenation is the operation of joining two character strings end-to-end. For example, the strings "snow" and "ball" may be concatenated to give "snowball"...
 of L and P
of L and P - the Kleene starKleene starIn mathematical logic and computer science, the Kleene star is a unary operation, either on sets of strings or on sets of symbols or characters. The application of the Kleene star to a set V is written as V*...
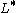 of L
of L - the image φ(L) of L under a homomorphism φ
- the image
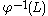 of L under an inverse homomorphism
of L under an inverse homomorphism 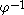
- the cyclic shift of L (the language
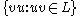 )
)
Context-free languages are not closed under complement
Complement (complexity)
In computational complexity theory, the complement of a decision problem is the decision problem resulting from reversing the yes and no answers. Equivalently, if we define decision problems as sets of finite strings, then the complement of this set over some fixed domain is its complement...
, intersection
Intersection (set theory)
In mathematics, the intersection of two sets A and B is the set that contains all elements of A that also belong to B , but no other elements....
, or difference. However, if L is a context-free language and D is a regular language then both their intersection
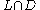 and their difference
and their difference 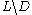 are context-free languages.
are context-free languages.Nonclosure under intersection and complement
The context-free languages are not closed under intersection. This can be seen by taking the languages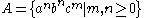 and
and 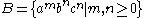 , which are both context-free. Their intersection is
, which are both context-free. Their intersection is 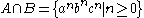 , which can be shown to be non-context-free by the pumping lemma for context-free languages
, which can be shown to be non-context-free by the pumping lemma for context-free languagesPumping lemma for context-free languages
The pumping lemma for context-free languages, also known as the Bar-Hillel lemma, is a lemma that gives a property shared by all context-free languages.- Formal statement :...
.
Context-free languages are also not closed under complementation, as for any languages A and B:
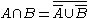 .
.Decidability properties
The following problems are undecidable for arbitrary context-free grammarContext-free grammar
In formal language theory, a context-free grammar is a formal grammar in which every production rule is of the formwhere V is a single nonterminal symbol, and w is a string of terminals and/or nonterminals ....
s A and B:
- Equivalence: is
 ?
? - is
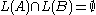 ? (However, the intersection of a context-free language and a regular language is context-free, so if
? (However, the intersection of a context-free language and a regular language is context-free, so if 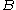 were a regular language, this problem becomes decidable.)
were a regular language, this problem becomes decidable.) - is
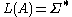 ?
? - is
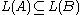 ?
?
The following problems are decidable for arbitrary context-free languages:
- is
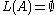 ?
? - is
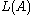 finite?
finite? - Membership: given any word
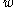 , does
, does 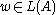 ? (membership problem is even polynomially decidable - see CYK algorithmCYK algorithmThe Cocke–Younger–Kasami algorithm is a parsing algorithm for context-free grammars. It employs bottom-up parsing and dynamic programming....
? (membership problem is even polynomially decidable - see CYK algorithmCYK algorithmThe Cocke–Younger–Kasami algorithm is a parsing algorithm for context-free grammars. It employs bottom-up parsing and dynamic programming....
and Early's Algorithm)
Properties of context-free languages
- The reverse of a context-free language is context-free, but the complement need not be.
- Every regular languageRegular languageIn theoretical computer science and formal language theory, a regular language is a formal language that can be expressed using regular expression....
is context-free because it can be described by a context-free grammarContext-free grammarIn formal language theory, a context-free grammar is a formal grammar in which every production rule is of the formwhere V is a single nonterminal symbol, and w is a string of terminals and/or nonterminals ....
. - The intersection of a context-free language and a regular language is always context-free.
- There exist context-sensitive languageContext-sensitive languageIn theoretical computer science, a context-sensitive language is a formal language that can be defined by a context-sensitive grammar. That is one of the four types of grammars in the Chomsky hierarchy...
s which are not context-free. - To prove that a given language is not context-free, one may employ the pumping lemma for context-free languagesPumping lemma for context-free languagesThe pumping lemma for context-free languages, also known as the Bar-Hillel lemma, is a lemma that gives a property shared by all context-free languages.- Formal statement :...
.

