
Connected category
Encyclopedia
In category theory
, a branch of mathematics
, a connected category is a category in which, for every two objects X and Y there is a finite sequence of objects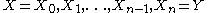
with morphisms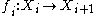
or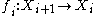
for each 0 ≤ i < n (both directions are allowed in the same sequence). Equivalently, a category J is connected if each functor
from J to a discrete category
is constant. In some cases it is convenient to not consider the empty category to be connected.
A stronger notion of connectivity would be to require at least one morphism f between any pair of objects X and Y. Clearly, any category which this property is connected in the above sense.
A small category is connected if and only if
its underlying graph is weakly connected.
Each category J can be written as a disjoint union (or coproduct
) of a connected categories, which are called the connected components of J. Each connected component is a full subcategory of J.
Category theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
, a branch of mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a connected category is a category in which, for every two objects X and Y there is a finite sequence of objects
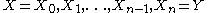
with morphisms
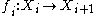
or
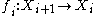
for each 0 ≤ i < n (both directions are allowed in the same sequence). Equivalently, a category J is connected if each functor
Functor
In category theory, a branch of mathematics, a functor is a special type of mapping between categories. Functors can be thought of as homomorphisms between categories, or morphisms when in the category of small categories....
from J to a discrete category
Discrete category
In mathematics, especially category theory, a discrete category is a category whose only morphisms are the identity morphisms. It is the simplest kind of category...
is constant. In some cases it is convenient to not consider the empty category to be connected.
A stronger notion of connectivity would be to require at least one morphism f between any pair of objects X and Y. Clearly, any category which this property is connected in the above sense.
A small category is connected if and only if
If and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
its underlying graph is weakly connected.
Each category J can be written as a disjoint union (or coproduct
Coproduct
In category theory, the coproduct, or categorical sum, is the category-theoretic construction which includes the disjoint union of sets and of topological spaces, the free product of groups, and the direct sum of modules and vector spaces. The coproduct of a family of objects is essentially the...
) of a connected categories, which are called the connected components of J. Each connected component is a full subcategory of J.

