
Comoving distance
Encyclopedia
In standard cosmology
, comoving distance and proper distance are two closely related distance measures used by cosmologists
to define distances between objects. Proper distance roughly corresponds to where a distant object would be at a specific moment of cosmological time, measured using a long series of rulers stretched out from our position to the object's position at that time, and which can change over time due to the expansion of the universe
. Comoving distance factors out the expansion of the universe, giving a distance that does not change in time due to the expansion of space. Comoving distance and proper distance are defined to be equal at the present time.
A comoving observer is the only observer that will perceive the universe, including the cosmic microwave background radiation
, to be isotropic. Non-comoving observers will see regions of the sky systematically blue-shifted or red-shifted. Thus isotropy, particularly isotropy of the cosmic microwave background radiation, defines a special local frame of reference
called the comoving frame. The velocity of an observer relative to the local comoving frame is called the peculiar velocity
of the observer.
Most large lumps of matter, such as galaxies, are nearly comoving, i.e., their peculiar velocities (due to gravitational attraction) are low.
The comoving time coordinate is the elapsed time since the Big Bang
according to a clock of a comoving observer and is a measure of cosmological time. The comoving spatial coordinates tell us where an event occurs while cosmological time tells us when an event occurs. Together, they form a complete coordinate system
, giving us both the location and time of an event.
Space in comoving coordinates is usually referred to as being "static", as most bodies on the scale of galaxies or larger are approximately comoving, and comoving bodies have static, unchanging comoving coordinates. So for a given pair of comoving galaxies, while the proper distance between them would have been smaller in the past and will become larger in the future due to the expansion of space, the comoving distance between them remains constant at all times.
The expanding Universe has an increasing scale factor which explains how constant comoving distances are reconciled with proper distances that increase with time.
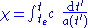
where a(t′) is the scale factor, te is the time of emission of the photons detected by the observer, t is the present time, and c is the speed of light
in vacuum.
Despite being an integral over time, this does give the distance that would be measured by a hypothetical tape measure at fixed time t, i.e. the "proper distance" as defined below, divided by the scale factor a(t) at that time. For a derivation see (Davis and Lineweaver, 2003) "standard relativistic definitions".
Definitions
It is important to the definition of both comoving distance and proper distance in the cosmological sense (as opposed to proper length
in special relativity
) that all observers have the same cosmological age. For instance, if one measured the distance along a straight line or spacelike geodesic
between the two points, observers situated between the two points would have different cosmological ages when the geodesic path crossed their own world line
s, so in calculating the distance along this geodesic one would not be correctly measuring comoving distance or cosmological proper distance. Comoving and proper distances are not the same concept of distance as the concept of distance in special relativity. This can be seen by considering the hypothetical case of a universe empty of mass, where both sorts of distance can be measured. When the density of mass in the FLRW metric is set to zero (an empty 'Milne universe'), then the cosmological coordinate system used to write this metric becomes a non-inertial coordinate system in the flat Minkowski spacetime
of special relativity, one where surfaces of constant time-coordinate appear as hyperbola
s when drawn in a Minkowski diagram
from the perspective of an inertial frame of reference
. In this case, for two events which are simultaneous according the cosmological time coordinate, the value of the cosmological proper distance is not equal to the value of the proper length
between these same events,(Wright) which would just be the distance along a straight line between the events in a Minkowski diagram (and a straight line is a geodesic
in flat Minkowski spacetime), or the coordinate distance between the events in the inertial frame where they are simultaneous
.
If one divides a change in proper distance by the interval of cosmological time where the change was measured (or takes the derivative
of proper distance with respect to cosmological time) and calls this a "velocity", then the resulting "velocities" of galaxies or quasars can be above the speed of light, c. This apparent superluminal expansion is not in conflict with special or general relativity, and is a consequence of the particular definitions used in cosmology. Even light itself does not have a "velocity" of c in this sense; the total velocity of any object can be expressed as the sum where
where 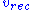 is the recession velocity due to the expansion of the universe (the velocity given by Hubble's law
is the recession velocity due to the expansion of the universe (the velocity given by Hubble's law
) and is the "peculiar velocity" measured by local observers (with
is the "peculiar velocity" measured by local observers (with  and
and 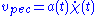 , the dots indicating a first derivative
, the dots indicating a first derivative
), so for light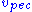 is equal to c (-c if the light is emitted towards our position at the origin and +c if emitted away from us) but the total velocity
is equal to c (-c if the light is emitted towards our position at the origin and +c if emitted away from us) but the total velocity  is generally different than c.(Davis and Lineweaver 2003, p. 19) Even in special relativity the coordinate speed of light is only guaranteed to be c in an inertial frame
is generally different than c.(Davis and Lineweaver 2003, p. 19) Even in special relativity the coordinate speed of light is only guaranteed to be c in an inertial frame
, in a non-inertial frame the coordinate speed may be different than c; in general relativity no coordinate system on a large region of curved spacetime is "inertial", but in the local neighborhood of any point in curved spacetime we can define a "local inertial frame" and the local speed of light will be c in this frame, with massive objects such as stars and galaxies always having a local speed smaller than c. The cosmological definitions used to define the velocities of distant objects are coordinate-dependent - there is no general coordinate-independent definition of velocity between distant objects in general relativity (Baez and Bunn, 2006). The issue of how best to describe and popularize the apparent superluminal expansion of the universe has caused a minor amount of controversy. One viewpoint is presented in (Davis and Lineweaver, 2003).
Big Bang
The Big Bang theory is the prevailing cosmological model that explains the early development of the Universe. According to the Big Bang theory, the Universe was once in an extremely hot and dense state which expanded rapidly. This rapid expansion caused the young Universe to cool and resulted in...
, comoving distance and proper distance are two closely related distance measures used by cosmologists
Distance measures (cosmology)
Distance measures are used in physical cosmology to give a natural notion of the distance between two objects or events in the universe. They are often used to tie some observable quantity to another quantity that is not directly...
to define distances between objects. Proper distance roughly corresponds to where a distant object would be at a specific moment of cosmological time, measured using a long series of rulers stretched out from our position to the object's position at that time, and which can change over time due to the expansion of the universe
Metric expansion of space
The metric expansion of space is the increase of distance between distant parts of the universe with time. It is an intrinsic expansion—that is, it is defined by the relative separation of parts of the universe and not by motion "outward" into preexisting space...
. Comoving distance factors out the expansion of the universe, giving a distance that does not change in time due to the expansion of space. Comoving distance and proper distance are defined to be equal at the present time.
Comoving coordinates
While general relativity allows one to formulate the laws of physics using arbitrary coordinates, some coordinate choices are more natural (e.g. they are easier to work with). Comoving coordinates are an example of such a natural coordinate choice. They assign constant spatial coordinate values to observers who perceive the universe as isotropic. Such observers are called "comoving" observers because they move along with the Hubble flow.A comoving observer is the only observer that will perceive the universe, including the cosmic microwave background radiation
Cosmic microwave background radiation
In cosmology, cosmic microwave background radiation is thermal radiation filling the observable universe almost uniformly....
, to be isotropic. Non-comoving observers will see regions of the sky systematically blue-shifted or red-shifted. Thus isotropy, particularly isotropy of the cosmic microwave background radiation, defines a special local frame of reference
Frame of reference
A frame of reference in physics, may refer to a coordinate system or set of axes within which to measure the position, orientation, and other properties of objects in it, or it may refer to an observational reference frame tied to the state of motion of an observer.It may also refer to both an...
called the comoving frame. The velocity of an observer relative to the local comoving frame is called the peculiar velocity
Peculiar velocity
Peculiar motion or peculiar velocity refers to the true velocity of an object, relative to a rest frame.-Galactic astronomy:In galactic astronomy, the term peculiar motion refers to the motion of an object through space.Local objects are usually related in terms of proper motion and radial...
of the observer.
Most large lumps of matter, such as galaxies, are nearly comoving, i.e., their peculiar velocities (due to gravitational attraction) are low.
The comoving time coordinate is the elapsed time since the Big Bang
Big Bang
The Big Bang theory is the prevailing cosmological model that explains the early development of the Universe. According to the Big Bang theory, the Universe was once in an extremely hot and dense state which expanded rapidly. This rapid expansion caused the young Universe to cool and resulted in...
according to a clock of a comoving observer and is a measure of cosmological time. The comoving spatial coordinates tell us where an event occurs while cosmological time tells us when an event occurs. Together, they form a complete coordinate system
Coordinate system
In geometry, a coordinate system is a system which uses one or more numbers, or coordinates, to uniquely determine the position of a point or other geometric element. The order of the coordinates is significant and they are sometimes identified by their position in an ordered tuple and sometimes by...
, giving us both the location and time of an event.
Space in comoving coordinates is usually referred to as being "static", as most bodies on the scale of galaxies or larger are approximately comoving, and comoving bodies have static, unchanging comoving coordinates. So for a given pair of comoving galaxies, while the proper distance between them would have been smaller in the past and will become larger in the future due to the expansion of space, the comoving distance between them remains constant at all times.
The expanding Universe has an increasing scale factor which explains how constant comoving distances are reconciled with proper distances that increase with time.
- See also: metric expansion of spaceMetric expansion of spaceThe metric expansion of space is the increase of distance between distant parts of the universe with time. It is an intrinsic expansion—that is, it is defined by the relative separation of parts of the universe and not by motion "outward" into preexisting space...
.
Comoving distance and proper distance
Comoving distance is the distance between two points measured along a path defined at the present cosmological time. For objects moving with the Hubble flow, it is deemed to remain constant in time. The comoving distance from an observer to a distant object (e.g. galaxy) can be computed by the following formula: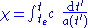
where a(t′) is the scale factor, te is the time of emission of the photons detected by the observer, t is the present time, and c is the speed of light
Speed of light
The speed of light in vacuum, usually denoted by c, is a physical constant important in many areas of physics. Its value is 299,792,458 metres per second, a figure that is exact since the length of the metre is defined from this constant and the international standard for time...
in vacuum.
Despite being an integral over time, this does give the distance that would be measured by a hypothetical tape measure at fixed time t, i.e. the "proper distance" as defined below, divided by the scale factor a(t) at that time. For a derivation see (Davis and Lineweaver, 2003) "standard relativistic definitions".
Definitions
- Many textbooks use the symbol
 for the comoving distance. However, this
for the comoving distance. However, this  must be distinguished from the coordinate distance r in the commonly-used comoving coordinate system for a FLRW universe where the metric takes the form
must be distinguished from the coordinate distance r in the commonly-used comoving coordinate system for a FLRW universe where the metric takes the form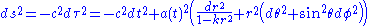 .
.
- In this case the comoving coordinate distance
 is related to
is related to  by
by  if k=0 (a spatially flat universe), by
if k=0 (a spatially flat universe), by  if k=1 (a positively-curved 'spherical' universe), and by
if k=1 (a positively-curved 'spherical' universe), and by 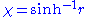 if k=-1 (a negatively-curved 'hyperbolic' universe).
if k=-1 (a negatively-curved 'hyperbolic' universe).
- Most textbooks and research papers define the comoving distance between comoving observers to be a fixed unchanging quantity independent of time, while calling the dynamic, changing distance between them proper distance. On this usage, comoving and proper distances are numerically equal at the current age of the universe, but will differ in the past and in the future; if the comoving distance to a galaxy is denoted
 , the proper distance
, the proper distance  at an arbitrary time
at an arbitrary time  is simply given by
is simply given by 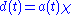 where
where 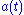 is the scale factor. (e.g. Davis and Lineweaver, 2003) The proper distance
is the scale factor. (e.g. Davis and Lineweaver, 2003) The proper distance 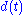 between two galaxies at time t is just the distance that would be measured by rulers between them at that time.
between two galaxies at time t is just the distance that would be measured by rulers between them at that time.
Uses of the proper distance
Cosmological time is identical to locally measured time for an observer at a fixed comoving spatial position, that is, in the local comoving frame. Proper distance is also equal to the locally measured distance in the comoving frame for nearby objects. To measure the proper distance between two distant objects, one imagines that one has many comoving observers in a straight line between the two objects, so that all of the observers are close to each other, and form a chain between the two distant objects. All of these observers must have the same cosmological time. Each observer measures their distance to the nearest observer in the chain, and the length of the chain, the sum of distances between nearby observers, is the total proper distance.It is important to the definition of both comoving distance and proper distance in the cosmological sense (as opposed to proper length
Proper length
In relativistic physics, proper length is an invariant measure of the distance between two spacelike-separated events, or of the length of a spacelike path within a spacetime....
in special relativity
Special relativity
Special relativity is the physical theory of measurement in an inertial frame of reference proposed in 1905 by Albert Einstein in the paper "On the Electrodynamics of Moving Bodies".It generalizes Galileo's...
) that all observers have the same cosmological age. For instance, if one measured the distance along a straight line or spacelike geodesic
Geodesic
In mathematics, a geodesic is a generalization of the notion of a "straight line" to "curved spaces". In the presence of a Riemannian metric, geodesics are defined to be the shortest path between points in the space...
between the two points, observers situated between the two points would have different cosmological ages when the geodesic path crossed their own world line
World line
In physics, the world line of an object is the unique path of that object as it travels through 4-dimensional spacetime. The concept of "world line" is distinguished from the concept of "orbit" or "trajectory" by the time dimension, and typically encompasses a large area of spacetime wherein...
s, so in calculating the distance along this geodesic one would not be correctly measuring comoving distance or cosmological proper distance. Comoving and proper distances are not the same concept of distance as the concept of distance in special relativity. This can be seen by considering the hypothetical case of a universe empty of mass, where both sorts of distance can be measured. When the density of mass in the FLRW metric is set to zero (an empty 'Milne universe'), then the cosmological coordinate system used to write this metric becomes a non-inertial coordinate system in the flat Minkowski spacetime
Minkowski space
In physics and mathematics, Minkowski space or Minkowski spacetime is the mathematical setting in which Einstein's theory of special relativity is most conveniently formulated...
of special relativity, one where surfaces of constant time-coordinate appear as hyperbola
Hyperbola
In mathematics a hyperbola is a curve, specifically a smooth curve that lies in a plane, which can be defined either by its geometric properties or by the kinds of equations for which it is the solution set. A hyperbola has two pieces, called connected components or branches, which are mirror...
s when drawn in a Minkowski diagram
Minkowski diagram
The Minkowski diagram was developed in 1908 by Hermann Minkowski and provides an illustration of the properties of space and time in the special theory of relativity. It allows a quantitative understanding of the corresponding phenomena like time dilation and length contraction without mathematical...
from the perspective of an inertial frame of reference
Inertial frame of reference
In physics, an inertial frame of reference is a frame of reference that describes time homogeneously and space homogeneously, isotropically, and in a time-independent manner.All inertial frames are in a state of constant, rectilinear motion with respect to one another; they are not...
. In this case, for two events which are simultaneous according the cosmological time coordinate, the value of the cosmological proper distance is not equal to the value of the proper length
Proper length
In relativistic physics, proper length is an invariant measure of the distance between two spacelike-separated events, or of the length of a spacelike path within a spacetime....
between these same events,(Wright) which would just be the distance along a straight line between the events in a Minkowski diagram (and a straight line is a geodesic
Geodesic
In mathematics, a geodesic is a generalization of the notion of a "straight line" to "curved spaces". In the presence of a Riemannian metric, geodesics are defined to be the shortest path between points in the space...
in flat Minkowski spacetime), or the coordinate distance between the events in the inertial frame where they are simultaneous
Relativity of simultaneity
In physics, the relativity of simultaneity is the concept that simultaneity–whether two events occur at the same time–is not absolute, but depends on the observer's reference frame. According to the special theory of relativity, it is impossible to say in an absolute sense whether two events occur...
.
If one divides a change in proper distance by the interval of cosmological time where the change was measured (or takes the derivative
Derivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
of proper distance with respect to cosmological time) and calls this a "velocity", then the resulting "velocities" of galaxies or quasars can be above the speed of light, c. This apparent superluminal expansion is not in conflict with special or general relativity, and is a consequence of the particular definitions used in cosmology. Even light itself does not have a "velocity" of c in this sense; the total velocity of any object can be expressed as the sum
 where
where 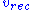 is the recession velocity due to the expansion of the universe (the velocity given by Hubble's law
is the recession velocity due to the expansion of the universe (the velocity given by Hubble's lawHubble's law
Hubble's law is the name for the astronomical observation in physical cosmology that: all objects observed in deep space are found to have a doppler shift observable relative velocity to Earth, and to each other; and that this doppler-shift-measured velocity, of various galaxies receding from...
) and
 is the "peculiar velocity" measured by local observers (with
is the "peculiar velocity" measured by local observers (with  and
and 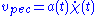 , the dots indicating a first derivative
, the dots indicating a first derivativeDerivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
), so for light
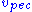 is equal to c (-c if the light is emitted towards our position at the origin and +c if emitted away from us) but the total velocity
is equal to c (-c if the light is emitted towards our position at the origin and +c if emitted away from us) but the total velocity  is generally different than c.(Davis and Lineweaver 2003, p. 19) Even in special relativity the coordinate speed of light is only guaranteed to be c in an inertial frame
is generally different than c.(Davis and Lineweaver 2003, p. 19) Even in special relativity the coordinate speed of light is only guaranteed to be c in an inertial frameInertial frame of reference
In physics, an inertial frame of reference is a frame of reference that describes time homogeneously and space homogeneously, isotropically, and in a time-independent manner.All inertial frames are in a state of constant, rectilinear motion with respect to one another; they are not...
, in a non-inertial frame the coordinate speed may be different than c; in general relativity no coordinate system on a large region of curved spacetime is "inertial", but in the local neighborhood of any point in curved spacetime we can define a "local inertial frame" and the local speed of light will be c in this frame, with massive objects such as stars and galaxies always having a local speed smaller than c. The cosmological definitions used to define the velocities of distant objects are coordinate-dependent - there is no general coordinate-independent definition of velocity between distant objects in general relativity (Baez and Bunn, 2006). The issue of how best to describe and popularize the apparent superluminal expansion of the universe has caused a minor amount of controversy. One viewpoint is presented in (Davis and Lineweaver, 2003).
Proper distance vs. comoving distance from small galaxies to galaxy clusters
Within small distances and short trips, the expansion of the universe during the trip can be ignored. This is because the travel time between any two points for a non-relativistic moving particle will just be the proper distance (i.e. the comoving distance measured using the scale factor of the universe at the time of the trip rather than the scale factor "now") between those points divided by the velocity of the particle. If the particle is moving at a relativistic velocity, the usual relativistic corrections for time dilation must be made.See also
- Distance measures (cosmology)Distance measures (cosmology)Distance measures are used in physical cosmology to give a natural notion of the distance between two objects or events in the universe. They are often used to tie some observable quantity to another quantity that is not directly...
for comparison with other distance measures - Friedmann–Lemaître–Robertson–Walker metric for information about the most popular cosmological model
- Shape of the universeShape of the UniverseThe shape of the universe is a matter of debate in physical cosmology over the local and global geometry of the universe which considers both curvature and topology, though, strictly speaking, it goes beyond both...
External links
- Distance measures in cosmology
- Ned Wright's cosmology tutorial
- iCosmos: Cosmology Calculator (With Graph Generation )
- Weinberg, Steven (1972)
- Peebles (1993)
- Davis and Lineweaver, Expanding Confusion
- Ned Wright's Javascript cosmology calculator
- General method, including locally inhomogeneous case and Fortran 77 software
- cosmdist-0.2.0 - command line and/or CC (programming language)C is a general-purpose computer programming language developed between 1969 and 1973 by Dennis Ritchie at the Bell Telephone Laboratories for use with the Unix operating system....
or FortranFortranFortran is a general-purpose, procedural, imperative programming language that is especially suited to numeric computation and scientific computing...
library, based on GNU Scientific LibraryGNU Scientific LibraryIn computing, the GNU Scientific Library is a software library written in the C programming language for numerical calculations in applied mathematics and science...
, for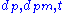 as functions of z and their inverses
as functions of z and their inverses

