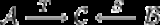
Comma category
Encyclopedia
In mathematics, a comma category (a special case being a slice category) is a construction in category theory
. It provides another way of looking at morphism
s: instead of simply relating objects of a category
to one another, morphisms become objects in their own right. This notion was introduced in 1963 by F. W. Lawvere
, although the technique did not become generally known until many years later. Today, it has become particularly important to mathematicians, because several important mathematical concepts can be treated as comma categories. There are also certain guarantees about the existence of limit
s and colimits in the context of comma categories. The name comes from the notation originally used by Lawvere, which involved the comma
punctuation mark. Although standard notation has changed since the use of a comma as an operator is potentially confusing, and even Lawvere dislikes the uninformative term "comma category", the name persists.
s with the same codomain. Often one of these will have domain 1 (the one-object one-morphism category). Some accounts of category theory consider these special cases only, but the term comma category is actually much more general.
 ,
,  , and
, and  are categories, and
are categories, and  and
and  are functor
are functor
s
We can form the comma category as follows:
as follows:
 Morphisms are composed by taking
Morphisms are composed by taking  to be
to be  , whenever the latter expression is defined. The identity morphism on an object
, whenever the latter expression is defined. The identity morphism on an object  is
is  .
.
 ,
,  is the identity functor, and
is the identity functor, and  (the category with one object
(the category with one object  and one morphism). Then
and one morphism). Then  for some object
for some object  in
in  . In this case, the comma category is written
. In this case, the comma category is written  , and is often called the slice category over
, and is often called the slice category over  or the category of objects over
or the category of objects over  . The objects
. The objects  can be simplified to pairs
can be simplified to pairs  , where
, where  . Sometimes,
. Sometimes,  is denoted
is denoted  . A morphism from
. A morphism from  to
to  in the slice category is then an arrow
in the slice category is then an arrow  making the following diagram commute:
making the following diagram commute:
concept to a slice category is a coslice category. Here, has domain 1 and
has domain 1 and  is an identity functor. In this case, the comma category is often written
is an identity functor. In this case, the comma category is often written
 , where
, where  is the object of
is the object of  selected by
selected by  . It is called the coslice category with respect to
. It is called the coslice category with respect to  , or the category of objects under
, or the category of objects under  . The objects are pairs
. The objects are pairs  with
with  . Given
. Given  and
and  , a morphism in the coslice category is a map
, a morphism in the coslice category is a map  making the following diagram commute:
making the following diagram commute:
 and
and  are identity functors on
are identity functors on  (so
(so  ). In this case, the comma category is the arrow category
). In this case, the comma category is the arrow category  . Its objects are the morphisms of
. Its objects are the morphisms of  , and its morphisms are commuting squares in
, and its morphisms are commuting squares in  .
.
 is the forgetful functor
is the forgetful functor
mapping an abelian group
to its underlying set, and is some fixed set (regarded as a functor from 1), then the comma category
is some fixed set (regarded as a functor from 1), then the comma category  has objects that are maps from
has objects that are maps from  to a set underlying a group. This relates to the left adjoint of
to a set underlying a group. This relates to the left adjoint of  , which is the functor that maps a set to the free abelian group
, which is the functor that maps a set to the free abelian group
having that set as its basis. In particular, the initial object of is the canonical injection
is the canonical injection  , where
, where  is the free group generated by
is the free group generated by  .
.
An object of is called a morphism from
is called a morphism from  to
to  or a
or a  -structured arrow with domain
-structured arrow with domain  in. An object of
in. An object of  is called a morphism from
is called a morphism from  to
to  or a
or a  -costructured arrow with codomain
-costructured arrow with codomain  in.
in.
Another special case occurs when both and
and  are functors with domain 1. If
are functors with domain 1. If  and
and  , then the comma category
, then the comma category  , written
, written  , is the discrete category
, is the discrete category
whose objects are morphisms from to
to  .
.
in comma categories may be "inherited". If and
and  are cocomplete,
are cocomplete,  is a cocontinuous functor, and
is a cocontinuous functor, and  another functor (not necessarily cocontinuous), then the comma category
another functor (not necessarily cocontinuous), then the comma category  produced will also be cocomplete. For example, in the above construction of the category of graphs, the category of sets is cocomplete, and the identity functor is cocontinuous: so graphs are also cocomplete - all (small) colimits exist. This result is much harder to obtain directly.
produced will also be cocomplete. For example, in the above construction of the category of graphs, the category of sets is cocomplete, and the identity functor is cocontinuous: so graphs are also cocomplete - all (small) colimits exist. This result is much harder to obtain directly.
If and
and  are complete, and both
are complete, and both  and
and  are continuous functors, then the comma category
are continuous functors, then the comma category  is also complete, and the projection functors
is also complete, and the projection functors  and
and  are limit preserving.
are limit preserving.
The notion of a universal morphism
to a particular colimit, or from a limit, can be expressed in terms of a comma category. Essentially, we create a category whose objects are cones, and where the limiting cone is a terminal object; then, each universal morphism for the limit is just the morphism to the terminal object. This works in the dual case, with a category of cocones having an initial object. For example, let be a category with
be a category with  the functor taking each object
the functor taking each object  to
to  and each arrow
and each arrow  to
to  . A universal morphism from
. A universal morphism from  to
to  consists, by definition, of an object
consists, by definition, of an object  and morphism
and morphism  with the universal property that for any morphism
with the universal property that for any morphism  there is a unique morphism
there is a unique morphism  with
with  . In other words, it is an object in the comma category
. In other words, it is an object in the comma category  having a morphism to any other object in that category; it is initial. This serves to define the coproduct
having a morphism to any other object in that category; it is initial. This serves to define the coproduct
in , when it exists.
, when it exists.
 and
and  are adjoint
are adjoint
if and only if the comma categories and
and  , with
, with  and
and  the identity functors on
the identity functors on  and
and  respectively, are isomorphic, and equivalent elements in the comma category can be projected onto the same element of
respectively, are isomorphic, and equivalent elements in the comma category can be projected onto the same element of  . This allows adjunctions to be described without involving sets, and was in fact the original motivation for introducing comma categories.
. This allows adjunctions to be described without involving sets, and was in fact the original motivation for introducing comma categories.
 are equal, then the diagram which defines morphisms in
are equal, then the diagram which defines morphisms in  with
with  is identical to the diagram which defines a natural transformation
is identical to the diagram which defines a natural transformation
 . The difference between the two notions is that a natural transformation is a particular collection of morphisms of type of the form
. The difference between the two notions is that a natural transformation is a particular collection of morphisms of type of the form  , while objects of the comma category contains all morphisms of type of such form. A functor to the comma category selects that particular collection of morphisms. This is described succinctly by an observation by Huq that a natural transformation
, while objects of the comma category contains all morphisms of type of such form. A functor to the comma category selects that particular collection of morphisms. This is described succinctly by an observation by Huq that a natural transformation  , with
, with  , corresponds to a functor
, corresponds to a functor  which maps each object
which maps each object  to
to  and maps each morphism
and maps each morphism  to
to  . This is a bijective
. This is a bijective
correspondence between natural transformations and functors
and functors  which are sections
which are sections
of both forgetful functors from .
.
Category theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
. It provides another way of looking at morphism
Morphism
In mathematics, a morphism is an abstraction derived from structure-preserving mappings between two mathematical structures. The notion of morphism recurs in much of contemporary mathematics...
s: instead of simply relating objects of a category
Category (mathematics)
In mathematics, a category is an algebraic structure that comprises "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose...
to one another, morphisms become objects in their own right. This notion was introduced in 1963 by F. W. Lawvere
William Lawvere
Francis William Lawvere is a mathematician known for his work in category theory, topos theory and the philosophy of mathematics.-Biography:...
, although the technique did not become generally known until many years later. Today, it has become particularly important to mathematicians, because several important mathematical concepts can be treated as comma categories. There are also certain guarantees about the existence of limit
Limit (category theory)
In category theory, a branch of mathematics, the abstract notion of a limit captures the essential properties of universal constructions such as products and inverse limits....
s and colimits in the context of comma categories. The name comes from the notation originally used by Lawvere, which involved the comma
Comma
A comma is a type of punctuation mark . The word comes from the Greek komma , which means something cut off or a short clause.Comma may also refer to:* Comma , a type of interval in music theory...
punctuation mark. Although standard notation has changed since the use of a comma as an operator is potentially confusing, and even Lawvere dislikes the uninformative term "comma category", the name persists.
Definition
The most general comma category construction involves two functorFunctor
In category theory, a branch of mathematics, a functor is a special type of mapping between categories. Functors can be thought of as homomorphisms between categories, or morphisms when in the category of small categories....
s with the same codomain. Often one of these will have domain 1 (the one-object one-morphism category). Some accounts of category theory consider these special cases only, but the term comma category is actually much more general.
General form
Suppose that ,
,  , and
, and  are categories, and
are categories, and  and
and  are functor
are functorFunctor
In category theory, a branch of mathematics, a functor is a special type of mapping between categories. Functors can be thought of as homomorphisms between categories, or morphisms when in the category of small categories....
s

We can form the comma category
 as follows:
as follows:
- The objects are all triples
 with
with  an object in
an object in  ,
,  an object in
an object in  , and
, and  a morphism in
a morphism in  .
. - The morphisms from
 to
to  are all pairs
are all pairs  where
where  and
and  are morphisms in
are morphisms in  and
and  respectively, such that the following diagram commutesCommutative diagramIn mathematics, and especially in category theory, a commutative diagram is a diagram of objects and morphisms such that all directed paths in the diagram with the same start and endpoints lead to the same result by composition...
respectively, such that the following diagram commutesCommutative diagramIn mathematics, and especially in category theory, a commutative diagram is a diagram of objects and morphisms such that all directed paths in the diagram with the same start and endpoints lead to the same result by composition...
:

 to be
to be  , whenever the latter expression is defined. The identity morphism on an object
, whenever the latter expression is defined. The identity morphism on an object  is
is  .
.Slice category
The first special case occurs when ,
,  is the identity functor, and
is the identity functor, and  (the category with one object
(the category with one object  and one morphism). Then
and one morphism). Then  for some object
for some object  in
in  . In this case, the comma category is written
. In this case, the comma category is written  , and is often called the slice category over
, and is often called the slice category over  or the category of objects over
or the category of objects over  . The objects
. The objects  can be simplified to pairs
can be simplified to pairs  , where
, where  . Sometimes,
. Sometimes,  is denoted
is denoted  . A morphism from
. A morphism from  to
to  in the slice category is then an arrow
in the slice category is then an arrow  making the following diagram commute:
making the following diagram commute:Coslice category
The dualDual (category theory)
In category theory, a branch of mathematics, duality is a correspondence between properties of a category C and so-called dual properties of the opposite category Cop...
concept to a slice category is a coslice category. Here,
 has domain 1 and
has domain 1 and  is an identity functor. In this case, the comma category is often written
is an identity functor. In this case, the comma category is often written , where
, where  is the object of
is the object of  selected by
selected by  . It is called the coslice category with respect to
. It is called the coslice category with respect to  , or the category of objects under
, or the category of objects under  . The objects are pairs
. The objects are pairs  with
with  . Given
. Given  and
and  , a morphism in the coslice category is a map
, a morphism in the coslice category is a map  making the following diagram commute:
making the following diagram commute:Arrow category
 and
and  are identity functors on
are identity functors on  (so
(so  ). In this case, the comma category is the arrow category
). In this case, the comma category is the arrow category  . Its objects are the morphisms of
. Its objects are the morphisms of  , and its morphisms are commuting squares in
, and its morphisms are commuting squares in  .
.Other variations
In the case of the slice or coslice category, the identity functor may be replaced with some other functor; this yields a family of categories particularly useful in the study of adjoint functors. For example, if is the forgetful functor
is the forgetful functorForgetful functor
In mathematics, in the area of category theory, a forgetful functor is a type of functor. The nomenclature is suggestive of such a functor's behaviour: given some object with structure as input, some or all of the object's structure or properties is 'forgotten' in the output...
mapping an abelian group
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
to its underlying set, and
 is some fixed set (regarded as a functor from 1), then the comma category
is some fixed set (regarded as a functor from 1), then the comma category  has objects that are maps from
has objects that are maps from  to a set underlying a group. This relates to the left adjoint of
to a set underlying a group. This relates to the left adjoint of  , which is the functor that maps a set to the free abelian group
, which is the functor that maps a set to the free abelian groupFree abelian group
In abstract algebra, a free abelian group is an abelian group that has a "basis" in the sense that every element of the group can be written in one and only one way as a finite linear combination of elements of the basis, with integer coefficients. Hence, free abelian groups over a basis B are...
having that set as its basis. In particular, the initial object of
 is the canonical injection
is the canonical injection  , where
, where  is the free group generated by
is the free group generated by  .
.An object of
 is called a morphism from
is called a morphism from  to
to  or a
or a  -structured arrow with domain
-structured arrow with domain  in. An object of
in. An object of  is called a morphism from
is called a morphism from  to
to  or a
or a  -costructured arrow with codomain
-costructured arrow with codomain  in.
in.Another special case occurs when both
 and
and  are functors with domain 1. If
are functors with domain 1. If  and
and  , then the comma category
, then the comma category  , written
, written  , is the discrete category
, is the discrete categoryDiscrete category
In mathematics, especially category theory, a discrete category is a category whose only morphisms are the identity morphisms. It is the simplest kind of category...
whose objects are morphisms from
 to
to  .
.Properties
For each comma category there are forgetful functors from it.- Domain functor,
 , which maps:
, which maps:
- objects:
 ;
; - morphisms:
 ;
;
- objects:
- Codomain functor,
 , which maps:
, which maps:
- objects:
 ;
; - morphisms:
 .
.
- objects:
Some notable categories
Several interesting categories have a natural definition in terms of comma categories.- The category of pointed setPointed setIn mathematics, a pointed set is a set X with a distinguished element x_0\in X, which is called the basepoint. Maps of pointed sets are those functions that map one basepoint to another, i.e. a map f : X \to Y such that f = y_0. This is usually denotedf : \to .Pointed sets may be regarded as a...
s is a comma category, with
with  being (a functor selecting) any singleton set, and
being (a functor selecting) any singleton set, and  (the identity functor of) the category of setsCategory of setsIn the mathematical field of category theory, the category of sets, denoted as Set, is the category whose objects are sets. The arrows or morphisms between sets A and B are all functions from A to B...
(the identity functor of) the category of setsCategory of setsIn the mathematical field of category theory, the category of sets, denoted as Set, is the category whose objects are sets. The arrows or morphisms between sets A and B are all functions from A to B...
. Each object of this category is a set, together with a function selecting some element of the set: the "basepoint". Morphisms are functions on sets which map basepoints to basepoints. In a similar fashion one can form the category of pointed spacePointed spaceIn mathematics, a pointed space is a topological space X with a distinguished basepoint x0 in X. Maps of pointed spaces are continuous maps preserving basepoints, i.e. a continuous map f : X → Y such that f = y0...
s .
. - The category of graphsGraph (mathematics)In mathematics, a graph is an abstract representation of a set of objects where some pairs of the objects are connected by links. The interconnected objects are represented by mathematical abstractions called vertices, and the links that connect some pairs of vertices are called edges...
is , with
, with  the functor taking a set
the functor taking a set  to
to  . The objects
. The objects  then consist of two sets and a function;
then consist of two sets and a function;  is an indexing set,
is an indexing set,  is a set of nodes, and
is a set of nodes, and  chooses pairs of elements of
chooses pairs of elements of  for each input from
for each input from  . That is,
. That is,  picks out certain edges from the set
picks out certain edges from the set  of possible edges. A morphism in this category is made up of two functions, one on the indexing set and one on the node set. They must "agree" according to the general definition above, meaning that
of possible edges. A morphism in this category is made up of two functions, one on the indexing set and one on the node set. They must "agree" according to the general definition above, meaning that  must satisfy
must satisfy  . In other words, the edge corresponding to a certain element of the indexing set, when translated, must be the same as the edge for the translated index.
. In other words, the edge corresponding to a certain element of the indexing set, when translated, must be the same as the edge for the translated index. - Many "augmentation" or "labelling" operations can be expressed in terms of comma categories. Let
 be the functor taking each graph to the set of its edges, and let
be the functor taking each graph to the set of its edges, and let  be (a functor selecting) some particular set: then
be (a functor selecting) some particular set: then  is the category of graphs whose edges are labelled by elements of
is the category of graphs whose edges are labelled by elements of  . This form of comma category is often called objects
. This form of comma category is often called objects  -over
-over  - closely related to the "objects over
- closely related to the "objects over  " discussed above. Here, each object takes the form
" discussed above. Here, each object takes the form  , where
, where  is a graph and
is a graph and  a function from the edges of
a function from the edges of  to
to  . The nodes of the graph could be labelled in essentially the same way.
. The nodes of the graph could be labelled in essentially the same way. - A category is said to be locally cartesian closed if every slice of it is cartesian closed (see above for the notion of slice). Locally cartesian closed categories are the classifying categories of dependent type theories.
Limits and universal morphisms
ColimitsLimit (category theory)
In category theory, a branch of mathematics, the abstract notion of a limit captures the essential properties of universal constructions such as products and inverse limits....
in comma categories may be "inherited". If
 and
and  are cocomplete,
are cocomplete,  is a cocontinuous functor, and
is a cocontinuous functor, and  another functor (not necessarily cocontinuous), then the comma category
another functor (not necessarily cocontinuous), then the comma category  produced will also be cocomplete. For example, in the above construction of the category of graphs, the category of sets is cocomplete, and the identity functor is cocontinuous: so graphs are also cocomplete - all (small) colimits exist. This result is much harder to obtain directly.
produced will also be cocomplete. For example, in the above construction of the category of graphs, the category of sets is cocomplete, and the identity functor is cocontinuous: so graphs are also cocomplete - all (small) colimits exist. This result is much harder to obtain directly.If
 and
and  are complete, and both
are complete, and both  and
and  are continuous functors, then the comma category
are continuous functors, then the comma category  is also complete, and the projection functors
is also complete, and the projection functors  and
and  are limit preserving.
are limit preserving.The notion of a universal morphism
Universal property
In various branches of mathematics, a useful construction is often viewed as the “most efficient solution” to a certain problem. The definition of a universal property uses the language of category theory to make this notion precise and to study it abstractly.This article gives a general treatment...
to a particular colimit, or from a limit, can be expressed in terms of a comma category. Essentially, we create a category whose objects are cones, and where the limiting cone is a terminal object; then, each universal morphism for the limit is just the morphism to the terminal object. This works in the dual case, with a category of cocones having an initial object. For example, let
 be a category with
be a category with  the functor taking each object
the functor taking each object  to
to  and each arrow
and each arrow  to
to  . A universal morphism from
. A universal morphism from  to
to  consists, by definition, of an object
consists, by definition, of an object  and morphism
and morphism  with the universal property that for any morphism
with the universal property that for any morphism  there is a unique morphism
there is a unique morphism  with
with  . In other words, it is an object in the comma category
. In other words, it is an object in the comma category  having a morphism to any other object in that category; it is initial. This serves to define the coproduct
having a morphism to any other object in that category; it is initial. This serves to define the coproductCoproduct
In category theory, the coproduct, or categorical sum, is the category-theoretic construction which includes the disjoint union of sets and of topological spaces, the free product of groups, and the direct sum of modules and vector spaces. The coproduct of a family of objects is essentially the...
in
 , when it exists.
, when it exists.Adjunctions
Lawvere showed that the functors and
and  are adjoint
are adjointAdjoint functors
In mathematics, adjoint functors are pairs of functors which stand in a particular relationship with one another, called an adjunction. The relationship of adjunction is ubiquitous in mathematics, as it rigorously reflects the intuitive notions of optimization and efficiency...
if and only if the comma categories
 and
and  , with
, with  and
and  the identity functors on
the identity functors on  and
and  respectively, are isomorphic, and equivalent elements in the comma category can be projected onto the same element of
respectively, are isomorphic, and equivalent elements in the comma category can be projected onto the same element of  . This allows adjunctions to be described without involving sets, and was in fact the original motivation for introducing comma categories.
. This allows adjunctions to be described without involving sets, and was in fact the original motivation for introducing comma categories.Natural transformations
If the domains of are equal, then the diagram which defines morphisms in
are equal, then the diagram which defines morphisms in  with
with  is identical to the diagram which defines a natural transformation
is identical to the diagram which defines a natural transformationNatural transformation
In category theory, a branch of mathematics, a natural transformation provides a way of transforming one functor into another while respecting the internal structure of the categories involved. Hence, a natural transformation can be considered to be a "morphism of functors". Indeed this intuition...
 . The difference between the two notions is that a natural transformation is a particular collection of morphisms of type of the form
. The difference between the two notions is that a natural transformation is a particular collection of morphisms of type of the form  , while objects of the comma category contains all morphisms of type of such form. A functor to the comma category selects that particular collection of morphisms. This is described succinctly by an observation by Huq that a natural transformation
, while objects of the comma category contains all morphisms of type of such form. A functor to the comma category selects that particular collection of morphisms. This is described succinctly by an observation by Huq that a natural transformation  , with
, with  , corresponds to a functor
, corresponds to a functor  which maps each object
which maps each object  to
to  and maps each morphism
and maps each morphism  to
to  . This is a bijective
. This is a bijectiveBijection
A bijection is a function giving an exact pairing of the elements of two sets. A bijection from the set X to the set Y has an inverse function from Y to X. If X and Y are finite sets, then the existence of a bijection means they have the same number of elements...
correspondence between natural transformations
 and functors
and functors  which are sections
which are sectionsSection (category theory)
In category theory, a branch of mathematics, a section is a right inverse of a morphism. Dually, a retraction is a left inverse...
of both forgetful functors from
 .
.

