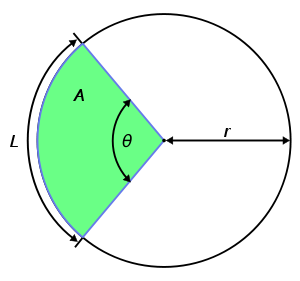
A circular sector or circle sector, is the portion of a disk

Disk (mathematics)

In geometry, a disk is the region in a plane bounded by a circle.A disk is said to be closed or open according to whether or not it contains the circle that constitutes its boundary...

 enclosed by two radii

Radius

In classical geometry, a radius of a circle or sphere is any line segment from its center to its perimeter. By extension, the radius of a circle or sphere is the length of any such segment, which is half the diameter. If the object does not have an obvious center, the term may refer to its...

 and an arc

Arc (geometry)

In geometry, an arc is a closed segment of a differentiable curve in the two-dimensional plane; for example, a circular arc is a segment of the circumference of a circle...

, where the smaller area is known as the minor sector and the larger being the major sector. In the diagram, θ is the central angle

Central angle

A central angle is an angle which vertex is the center of a circle, and whose sides pass through a pair of points on the circle, thereby subtending an arc between those two points whose angle is equal to the central angle itself...

 in radian

Radian

Radian is the ratio between the length of an arc and its radius. The radian is the standard unit of angular measure, used in many areas of mathematics. The unit was formerly a SI supplementary unit, but this category was abolished in 1995 and the radian is now considered a SI derived unit...

s, $r$ the radius of the circle, and $L$ is the arc length of the minor sector. A sector with the central angle of 180° is called a semicircle

Semicircle

In mathematics , a semicircle is a two-dimensional geometric shape that forms half of a circle. Being half of a circle's 360°, the arc of a semicircle always measures 180° or a half turn...

. Sectors with other central angles are sometimes given special names, these include quadrants (90°), sextants (60°) and octants (45°). The angle formed by connecting the endpoints of the arc to any point on the circumference that is not in the sector is equal to half the central angle.

Area

The total area of a circle is $\backslash pi\; r^2$. The area of the sector can be obtained by multiplying the circle's area by the ratio of the angle and $2\; \backslash pi$ (because the area of the sector is proportional to the angle, and $2\; \backslash pi$ is the angle for the whole circle): $A\; =\; \backslash pi\; r^2\; \backslash cdot\; \backslash frac\{\backslash theta\}\{2\; \backslash pi\}\; =\; \backslash frac\{r^2\; \backslash theta\}\{2\}$ Another approach is to consider this area as the result of the following integral :$A\; =\; \backslash int\_0^\backslash theta\backslash int\_0^r\; dS=\backslash int\_0^\backslash theta\backslash int\_0^r\; \backslash tilde\{r\}\; d\backslash tilde\{r\}\; d\backslash tilde\{\backslash theta\}\; =\; \backslash int\_0^\backslash theta\; \backslash frac\{1\}\{2\}\; r^2\; d\backslash tilde\{\backslash theta\}\; =\; \backslash frac\{r^2\; \backslash theta\}\{2\}$ Converting the central angle into degree

Degree (angle)

A degree , usually denoted by ° , is a measurement of plane angle, representing 1⁄360 of a full rotation; one degree is equivalent to π/180 radians...

s gives$A\; =\; \backslash pi\; r^2\; \backslash cdot\; \backslash frac\{\backslash theta\; ^\{\backslash circ\}\}\{360\}$

Perimeter

The length of the perimeter

Perimeter

A perimeter is a path that surrounds an area. The word comes from the Greek peri and meter . The term may be used either for the path or its length - it can be thought of as the length of the outline of a shape. The perimeter of a circular area is called circumference.- Practical uses :Calculating...

 of a sector is the sum of the arc length and the two radii:$P$

Center of Mass

The distance from the center of the circle (that the sector is a part of) to the center of mass of the sector is two thirds of the corresponding distance for the center of mass of the arc of the sector. In particular, as the central angle approaches zero the center of mass of the arc is at distance r from the center of the circle, so that of the sector is at distance 2r/3. As the central angle approaches 2π (the whole circle), the center of mass of the arc converges to the center of the circle, whence so does that of the circular sector.

See also

NEWLINE

NEWLINE
• Circular segment
  Circular segment
  In geometry, a circular segment is an area of a circle informally defined as an area which is "cut off" from the rest of the circle by a secant or a chord. The circle segment constitutes the part between the secant and an arc, excluding the circle's center...
  
   - the part of the sector which remains after removing the triangle formed by the center of the circle and the two endpoints of the circular arc on the boundary.
NEWLINE
• Conic section
  Conic section
  In mathematics, a conic section is a curve obtained by intersecting a cone with a plane. In analytic geometry, a conic may be defined as a plane algebraic curve of degree 2...
  
  
NEWLINE
• Hyperbolic sector

NEWLINE

External links

NEWLINE

NEWLINE
• Definition and properties of a circle sector with interactive animation

NEWLINE