
Choquet theory
Encyclopedia
In mathematics
, Choquet theory is an area of functional analysis
and convex analysis
created by Gustave Choquet
. It is concerned with measures
with support
on the extreme points of a convex set
C. Roughly speaking, all vectors of C should appear as 'averages' of extreme points, a concept made more precise by the idea of convex combination
s replaced by integral
s taken over the set E of extreme points. Here C is a subset of a real vector space V, and the main thrust of the theory is to treat the cases where V is an infinite-dimensional (locally convex Hausdorff) topological vector space
along lines similar to the finite-dimensional case. The main concerns of Gustave Choquet were in potential theory
. Choquet theory has become a general paradigm, particularly for treating convex cone
s as determined by their extreme rays, and so for many different notions of positivity in mathematics.
The two ends of a line segment
determine the points in between: in vector terms the segment from v to w consists of the λv + (1 − λ)w with 0 ≤ λ ≤ 1. The classical result of Hermann Minkowski
says that in Euclidean space
, a bounded
, closed
convex set
C is the convex hull
of its extreme point set E, so that any c in C is a (finite) convex combination
of points e of E. Here E may be a finite or an infinite set. In vector terms, by assigning non-negative weights w(e) to the e in E, almost all
0, we can represent any c in C as

with

In any case the w(e) give a probability measure
supported on a finite subset of E. For any affine function f on C, its value at the point c is

In the infinite dimensional setting, one would like to make a similar statement.
Choquet's theorem states that for a compact convex subset C in a normed space V, given c in C there exist a probability measure
w supported on the set E of extreme points of C such that, for all affine function f on C.
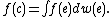
In practice V will be a Banach space
. The original Krein–Milman theorem follows from Choquet's result. Another corollary is the Riesz representation theorem
for states
on the continuous functions on a metrizable compact Hausdorff space.
More generally, for V a locally convex topological vector space
, the Choquet-Bishop-de Leeuw theorem gives the same formal statement.
In addition to the existence of a probability measure supported on the extreme boundary that represent a given point c, one might also consider the uniqueness of such measures. It is easy to see that uniqueness does not hold even in the finite dimensional setting. One can take, for counterexamples, the convex set to be a cube
or a ball in R3. Uniqueness does hold, however, when the convex set is a finite dimensional simplex
. So that the weights w(e) are unique. A finite dimensional simplex is a special cases of a Choquet simplex. Any point in a Choquet simplex is represented by a unique probability measure on the extreme points.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, Choquet theory is an area of functional analysis
Functional analysis
Functional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure and the linear operators acting upon these spaces and respecting these structures in a suitable sense...
and convex analysis
Convex analysis
Convex analysis is the branch of mathematics devoted to the study of properties of convex functions and convex sets, often with applications in convex minimization, a subdomain of optimization theory....
created by Gustave Choquet
Gustave Choquet
Gustave Choquet was a French mathematician.Choquet was born in Solesmes, Nord. His contributions include work in functional analysis, potential theory, topology and measure theory...
. It is concerned with measures
Measure (mathematics)
In mathematical analysis, a measure on a set is a systematic way to assign to each suitable subset a number, intuitively interpreted as the size of the subset. In this sense, a measure is a generalization of the concepts of length, area, and volume...
with support
Support (mathematics)
In mathematics, the support of a function is the set of points where the function is not zero, or the closure of that set . This concept is used very widely in mathematical analysis...
on the extreme points of a convex set
Convex set
In Euclidean space, an object is convex if for every pair of points within the object, every point on the straight line segment that joins them is also within the object...
C. Roughly speaking, all vectors of C should appear as 'averages' of extreme points, a concept made more precise by the idea of convex combination
Convex combination
In convex geometry, a convex combination is a linear combination of points where all coefficients are non-negative and sum up to 1....
s replaced by integral
Integral
Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
s taken over the set E of extreme points. Here C is a subset of a real vector space V, and the main thrust of the theory is to treat the cases where V is an infinite-dimensional (locally convex Hausdorff) topological vector space
Topological vector space
In mathematics, a topological vector space is one of the basic structures investigated in functional analysis...
along lines similar to the finite-dimensional case. The main concerns of Gustave Choquet were in potential theory
Potential theory
In mathematics and mathematical physics, potential theory may be defined as the study of harmonic functions.- Definition and comments :The term "potential theory" was coined in 19th-century physics, when it was realized that the fundamental forces of nature could be modeled using potentials which...
. Choquet theory has become a general paradigm, particularly for treating convex cone
Convex cone
In linear algebra, a convex cone is a subset of a vector space over an ordered field that is closed under linear combinations with positive coefficients.-Definition:...
s as determined by their extreme rays, and so for many different notions of positivity in mathematics.
The two ends of a line segment
Line segment
In geometry, a line segment is a part of a line that is bounded by two end points, and contains every point on the line between its end points. Examples of line segments include the sides of a triangle or square. More generally, when the end points are both vertices of a polygon, the line segment...
determine the points in between: in vector terms the segment from v to w consists of the λv + (1 − λ)w with 0 ≤ λ ≤ 1. The classical result of Hermann Minkowski
Hermann Minkowski
Hermann Minkowski was a German mathematician of Ashkenazi Jewish descent, who created and developed the geometry of numbers and who used geometrical methods to solve difficult problems in number theory, mathematical physics, and the theory of relativity.- Life and work :Hermann Minkowski was born...
says that in Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
, a bounded
Bounded set
In mathematical analysis and related areas of mathematics, a set is called bounded, if it is, in a certain sense, of finite size. Conversely, a set which is not bounded is called unbounded...
, closed
Closed set
In geometry, topology, and related branches of mathematics, a closed set is a set whose complement is an open set. In a topological space, a closed set can be defined as a set which contains all its limit points...
convex set
Convex set
In Euclidean space, an object is convex if for every pair of points within the object, every point on the straight line segment that joins them is also within the object...
C is the convex hull
Convex hull
In mathematics, the convex hull or convex envelope for a set of points X in a real vector space V is the minimal convex set containing X....
of its extreme point set E, so that any c in C is a (finite) convex combination
Convex combination
In convex geometry, a convex combination is a linear combination of points where all coefficients are non-negative and sum up to 1....
of points e of E. Here E may be a finite or an infinite set. In vector terms, by assigning non-negative weights w(e) to the e in E, almost all
Almost all
In mathematics, the phrase "almost all" has a number of specialised uses."Almost all" is sometimes used synonymously with "all but finitely many" or "all but a countable set" ; see almost....
0, we can represent any c in C as

with

In any case the w(e) give a probability measure
Probability measure
In mathematics, a probability measure is a real-valued function defined on a set of events in a probability space that satisfies measure properties such as countable additivity...
supported on a finite subset of E. For any affine function f on C, its value at the point c is

In the infinite dimensional setting, one would like to make a similar statement.
Choquet's theorem states that for a compact convex subset C in a normed space V, given c in C there exist a probability measure
Probability measure
In mathematics, a probability measure is a real-valued function defined on a set of events in a probability space that satisfies measure properties such as countable additivity...
w supported on the set E of extreme points of C such that, for all affine function f on C.
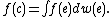
In practice V will be a Banach space
Banach space
In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
. The original Krein–Milman theorem follows from Choquet's result. Another corollary is the Riesz representation theorem
Riesz representation theorem
There are several well-known theorems in functional analysis known as the Riesz representation theorem. They are named in honour of Frigyes Riesz.- The Hilbert space representation theorem :...
for states
State (functional analysis)
In functional analysis, a state on a C*-algebra is a positive linear functional of norm 1. The set of states of a C*-algebra A, sometimes denoted by S, is always a convex set. The extremal points of S are called pure states...
on the continuous functions on a metrizable compact Hausdorff space.
More generally, for V a locally convex topological vector space
Locally convex topological vector space
In functional analysis and related areas of mathematics, locally convex topological vector spaces or locally convex spaces are examples of topological vector spaces which generalize normed spaces. They can be defined as topological vector spaces whose topology is generated by translations of ...
, the Choquet-Bishop-de Leeuw theorem gives the same formal statement.
In addition to the existence of a probability measure supported on the extreme boundary that represent a given point c, one might also consider the uniqueness of such measures. It is easy to see that uniqueness does not hold even in the finite dimensional setting. One can take, for counterexamples, the convex set to be a cube
Cube
In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and...
or a ball in R3. Uniqueness does hold, however, when the convex set is a finite dimensional simplex
Simplex
In geometry, a simplex is a generalization of the notion of a triangle or tetrahedron to arbitrary dimension. Specifically, an n-simplex is an n-dimensional polytope which is the convex hull of its n + 1 vertices. For example, a 2-simplex is a triangle, a 3-simplex is a tetrahedron,...
. So that the weights w(e) are unique. A finite dimensional simplex is a special cases of a Choquet simplex. Any point in a Choquet simplex is represented by a unique probability measure on the extreme points.
See also
- Carathéodory's theoremCarathéodory's theorem (convex hull)In convex geometry Carathéodory's theorem states that if a point x of Rd lies in the convex hull of a set P, there is a subset P′ of P consisting of d+1 or fewer points such that x lies in the convex hull of P′. Equivalently, x lies in an r-simplex with vertices in P, where r \leq d...
- Shapley–Folkman lemmaShapley–Folkman lemmaIn geometry and economics, the Shapley–Folkman lemma describes the Minkowski addition of sets in a vector space. Minkowski addition is defined as the addition of the sets' members: for example, adding the set consisting of the integers zero and one to itself yields the set consisting of...
- Krein–Milman theorem
- Helly's theoremHelly's theoremHelly's theorem is a basic result in discrete geometry describing the ways that convex sets may intersect each other. It was discovered by Eduard Helly in 1913, but not published by him until 1923, by which time alternative proofs by and had already appeared...

