
Change of variables (PDE)
Encyclopedia
Often a partial differential equation
can be reduced to a simpler form with a known solution by a suitable change of variables
.
The article discusses change of variable for PDEs below in two ways:
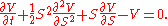
is reducible to the heat equation
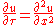
by the change of variables:
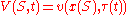

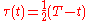
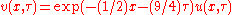
in these steps:
Partial differential equation
In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
can be reduced to a simpler form with a known solution by a suitable change of variables
Change of variables
In mathematics, a change of variables is a basic technique used to simplify problems in which the original variables are replaced with new ones; the new and old variables being related in some specified way...
.
The article discusses change of variable for PDEs below in two ways:
- by example;
- by giving the theory of the method.
Explanation by example
For example the following simplified form of the Black–Scholes PDE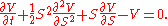
is reducible to the heat equation
Heat equation
The heat equation is an important partial differential equation which describes the distribution of heat in a given region over time...
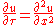
by the change of variables:
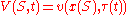

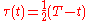
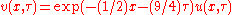
in these steps:
- Replace
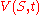 by
by 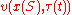 and apply the chain ruleChain ruleIn calculus, the chain rule is a formula for computing the derivative of the composition of two or more functions. That is, if f is a function and g is a function, then the chain rule expresses the derivative of the composite function in terms of the derivatives of f and g.In integration, the...
and apply the chain ruleChain ruleIn calculus, the chain rule is a formula for computing the derivative of the composition of two or more functions. That is, if f is a function and g is a function, then the chain rule expresses the derivative of the composite function in terms of the derivatives of f and g.In integration, the...
to get
-

- Replace
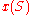 and
and  by
by 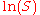 and
and 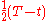 to get
to get
-
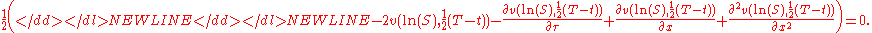
- Replace
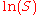 and
and 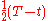 by
by 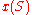 and
and  and divide both sides by
and divide both sides by  to get
to get
- Replace
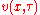 by
by 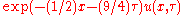 and divide through by
and divide through by 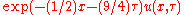 to yield the heat equation.
to yield the heat equation.
Advice on the application of change of variable to PDEs is given by mathematician J. Michael SteeleJ. Michael SteeleJohn Michael Steele is C.F. Koo Professor of Statistics at the Wharton School of the University of Pennsylvania, and he was previously affiliated with Stanford University, Columbia University and Princeton University....
:
Technique in general
Suppose that we have a function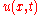 and a change of variables
and a change of variables 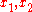 such that there exist functions
such that there exist functions 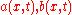 such that
such that
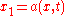
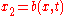
and functions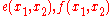 such that
such that

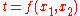
and furthermore such that
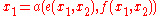
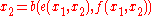
and
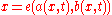
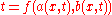
In other words, it is helpful for there to be a bijectionBijectionA bijection is a function giving an exact pairing of the elements of two sets. A bijection from the set X to the set Y has an inverse function from Y to X. If X and Y are finite sets, then the existence of a bijection means they have the same number of elements...
between the old set of variables and the new one, or else one has to- Restrict the domain of applicability of the correspondence to a subject of the real plane which is sufficient for a solution of the practical problem at hand (where again it needs to be a bijection), and
- Enumerate the (zero or more finite list) of exceptions (poles) where the otherwise-bijection fails (and say why these exceptions don't restrict the applicability of the solution of the reduced equation to the original equation)
If a bijection does not exist then the solution to the reduced-form equation will not in general be a solution of the original equation.
We are discussing change of variable for PDEs. A PDE can be expressed as a differential operatorDifferential operatorIn mathematics, a differential operator is an operator defined as a function of the differentiation operator. It is helpful, as a matter of notation first, to consider differentiation as an abstract operation, accepting a function and returning another .This article considers only linear operators,...
applied to a function. Suppose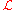 is a differential operator such that
is a differential operator such that
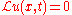
Then it is also the case that

where
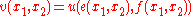
and we operate as follows to go from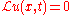 to
to 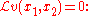
- Apply the chain ruleChain ruleIn calculus, the chain rule is a formula for computing the derivative of the composition of two or more functions. That is, if f is a function and g is a function, then the chain rule expresses the derivative of the composite function in terms of the derivatives of f and g.In integration, the...
to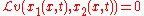 and expand out giving equation
and expand out giving equation 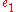 .
. - Substitute
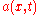 for
for 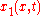 and
and 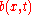 for
for 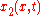 in
in 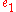 and expand out giving equation
and expand out giving equation 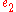 .
. - Replace occurrences of
 by
by 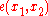 and
and  by
by 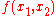 to yield
to yield  , which will be free of
, which will be free of  and
and  .
.
Action-angle coordinates
Often, theory can establish the existence of a change of variables, although the formula itself cannot be explicitly stated. For a integrable Hamiltonian system of dimension , with
, with 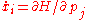 and
and 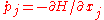 , there exist
, there exist  integrals
integrals 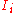 . There exists a change of variables from the coordinates
. There exists a change of variables from the coordinates 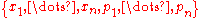 to a set of variables
to a set of variables 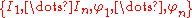 , in which the equations of motion become
, in which the equations of motion become  ,
, 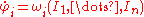 , where the functions
, where the functions  are unknown, but depend only on
are unknown, but depend only on  . The variables
. The variables  are the action coordinates, the variables
are the action coordinates, the variables  are the angle coordinates. The motion of the system can thus be visualized as rotation on torii. As a particular example, consider the simple harmonic oscillator, with
are the angle coordinates. The motion of the system can thus be visualized as rotation on torii. As a particular example, consider the simple harmonic oscillator, with 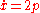 and
and 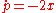 , with Hamiltonian
, with Hamiltonian  . This system can be rewritten as
. This system can be rewritten as  ,
,  , where
, where 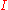 and
and 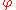 are the canonical polar coordinates:
are the canonical polar coordinates: 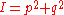 and
and 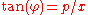 . See V. I. ArnoldVladimir ArnoldVladimir Igorevich Arnold was a Soviet and Russian mathematician. While he is best known for the Kolmogorov–Arnold–Moser theorem regarding the stability of integrable Hamiltonian systems, he made important contributions in several areas including dynamical systems theory, catastrophe theory,...
. See V. I. ArnoldVladimir ArnoldVladimir Igorevich Arnold was a Soviet and Russian mathematician. While he is best known for the Kolmogorov–Arnold–Moser theorem regarding the stability of integrable Hamiltonian systems, he made important contributions in several areas including dynamical systems theory, catastrophe theory,...
, `Mathematical Methods of Classical Mechanics', for more details.- Replace
- Replace


