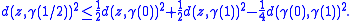Cartan–Hadamard theorem
Encyclopedia
The Cartan–Hadamard theorem is a statement in Riemannian geometry
concerning the structure of complete Riemannian manifold
s of non-positive sectional curvature
. The theorem states that the universal cover of such a manifold is diffeomorphic to a Euclidean space
via the exponential map
at any point. It was first proved by Hans Carl Friedrich von Mangoldt
for surface
s in 1881, and independently by Jacques Hadamard
in 1898. Élie Cartan
generalized the theorem to Riemannian manifolds in 1928 . The theorem was further generalized to a wide class of metric space
s by Mikhail Gromov in 1987; detailed proofs were published by for metric spaces of non-positive curvature and by for general locally convex spaces.
complete Riemannian manifold
of non-positive sectional curvature
is diffeomorphic
to Rn. In fact, for complete manifolds on non-positive curvature the exponential map
based at any point of the manifold is a covering map.
The theorem holds also for Hilbert manifold
s in the sense that the exponential map of a non-positively curved geodesically complete connected manifold is a covering map . Completeness here is understood in the sense that the exponential map is defined on the whole tangent space
of a point.
non-positively curved complete metric space X is a Hadamard space. In particular, if X is simply connected then it is a geodesic space in the sense that any two points are connected by a unique minimizing geodesic, and hence contractible.
A metric space X is said to be non-positively curved if every point p has a neighborhood U in which any two points are joined by a geodesic
, and for any point z in U and constant speed geodesic γ in U, one has
This inequality may be usefully thought of in terms of a geodesic triangle Δ = zγ(0)γ(1). The left-hand side is the square distance from the vertex z to the midpoint of the opposite side. The right-hand side represents the square distance from the vertex to the midpoint of the opposite side in a Euclidean triangle having the same side lengths as Δ. This condition, called the CAT(0) condition
is an abstract form of Toponogov's triangle comparison theorem
.
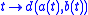
is a convex function
of t. A metric space is then locally convex if every point has a neighborhood that is convex in this sense. The Cartan–Hadamard theorem for locally convex spaces states:
In particular, the universal covering of such a space is contractible. The convexity of the distance function along a pair of geodesics is a well-known consequence of non-positive curvature of a metric space, but it is not equivalent .
The metric form of the theorem demonstrates that a non-positively curved polyhedral cell complex is aspherical
. This fact is of crucial importance for modern geometric group theory
.
Riemannian geometry
Riemannian geometry is the branch of differential geometry that studies Riemannian manifolds, smooth manifolds with a Riemannian metric, i.e. with an inner product on the tangent space at each point which varies smoothly from point to point. This gives, in particular, local notions of angle, length...
concerning the structure of complete Riemannian manifold
Riemannian manifold
In Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...
s of non-positive sectional curvature
Sectional curvature
In Riemannian geometry, the sectional curvature is one of the ways to describe the curvature of Riemannian manifolds. The sectional curvature K depends on a two-dimensional plane σp in the tangent space at p...
. The theorem states that the universal cover of such a manifold is diffeomorphic to a Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
via the exponential map
Exponential map
In differential geometry, the exponential map is a generalization of the ordinary exponential function of mathematical analysis to all differentiable manifolds with an affine connection....
at any point. It was first proved by Hans Carl Friedrich von Mangoldt
Hans Carl Friedrich von Mangoldt
Hans Carl Friedrich von Mangoldt was a German mathematician who contributed to the solution of the prime number theorem.Von Mangoldt completed his Doctor of Philosophy in 1878 at the University of Berlin, where his advisors were Ernst Kummer and Karl Weierstrass...
for surface
Surface
In mathematics, specifically in topology, a surface is a two-dimensional topological manifold. The most familiar examples are those that arise as the boundaries of solid objects in ordinary three-dimensional Euclidean space R3 — for example, the surface of a ball...
s in 1881, and independently by Jacques Hadamard
Jacques Hadamard
Jacques Salomon Hadamard FRS was a French mathematician who made major contributions in number theory, complex function theory, differential geometry and partial differential equations.-Biography:...
in 1898. Élie Cartan
Élie Cartan
Élie Joseph Cartan was an influential French mathematician, who did fundamental work in the theory of Lie groups and their geometric applications...
generalized the theorem to Riemannian manifolds in 1928 . The theorem was further generalized to a wide class of metric space
Metric space
In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
s by Mikhail Gromov in 1987; detailed proofs were published by for metric spaces of non-positive curvature and by for general locally convex spaces.
Riemannian geometry
The Cartan–Hadamard theorem in conventional Riemannian geometry asserts that the universal covering space of a connectedConnected space
In topology and related branches of mathematics, a connected space is a topological space that cannot be represented as the union of two or more disjoint nonempty open subsets. Connectedness is one of the principal topological properties that is used to distinguish topological spaces...
complete Riemannian manifold
Riemannian manifold
In Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...
of non-positive sectional curvature
Sectional curvature
In Riemannian geometry, the sectional curvature is one of the ways to describe the curvature of Riemannian manifolds. The sectional curvature K depends on a two-dimensional plane σp in the tangent space at p...
is diffeomorphic
Diffeomorphism
In mathematics, a diffeomorphism is an isomorphism in the category of smooth manifolds. It is an invertible function that maps one differentiable manifold to another, such that both the function and its inverse are smooth.- Definition :...
to Rn. In fact, for complete manifolds on non-positive curvature the exponential map
Exponential map
In differential geometry, the exponential map is a generalization of the ordinary exponential function of mathematical analysis to all differentiable manifolds with an affine connection....
based at any point of the manifold is a covering map.
The theorem holds also for Hilbert manifold
Hilbert manifold
In mathematics, a Hilbert manifold is a manifold modeled on Hilbert spaces. Thus it is a separable Hausdorff space in which each point has a neighbourhood homeomorphic to an infinite dimensional Hilbert space. The concept of a Hilbert manifold provides a possibility of extending the theory of...
s in the sense that the exponential map of a non-positively curved geodesically complete connected manifold is a covering map . Completeness here is understood in the sense that the exponential map is defined on the whole tangent space
Tangent space
In mathematics, the tangent space of a manifold facilitates the generalization of vectors from affine spaces to general manifolds, since in the latter case one cannot simply subtract two points to obtain a vector pointing from one to the other....
of a point.
Metric geometry
In metric geometry, the Cartan–Hadamard theorem is the statement that the universal cover of a connectedConnectedness
In mathematics, connectedness is used to refer to various properties meaning, in some sense, "all one piece". When a mathematical object has such a property, we say it is connected; otherwise it is disconnected...
non-positively curved complete metric space X is a Hadamard space. In particular, if X is simply connected then it is a geodesic space in the sense that any two points are connected by a unique minimizing geodesic, and hence contractible.
A metric space X is said to be non-positively curved if every point p has a neighborhood U in which any two points are joined by a geodesic
Geodesic
In mathematics, a geodesic is a generalization of the notion of a "straight line" to "curved spaces". In the presence of a Riemannian metric, geodesics are defined to be the shortest path between points in the space...
, and for any point z in U and constant speed geodesic γ in U, one has
This inequality may be usefully thought of in terms of a geodesic triangle Δ = zγ(0)γ(1). The left-hand side is the square distance from the vertex z to the midpoint of the opposite side. The right-hand side represents the square distance from the vertex to the midpoint of the opposite side in a Euclidean triangle having the same side lengths as Δ. This condition, called the CAT(0) condition
CAT(k) space
In mathematics, a CAT space is a specific type of metric space. Intuitively, triangles in a CAT space are "slimmer" than corresponding "model triangles" in a standard space of constant curvature k. In a CAT space, the curvature is bounded from above by k...
is an abstract form of Toponogov's triangle comparison theorem
Toponogov's theorem
In the mathematical field of Riemannian geometry, Toponogov's theorem is a triangle comparison theorem. It is one of a family of theorems that quantify the assertion that a pair of geodesics emanating from a point p spread apart more slowly in a region of high curvature than they would in a region...
.
Generalization to locally convex spaces
The assumption of non-positive curvature can be weakened , although with a correspondingly weaker conclusion. Call a metric space X convex if, for any two constant speed minimizing geodesics a(t) and b(t), the function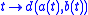
is a convex function
Convex function
In mathematics, a real-valued function f defined on an interval is called convex if the graph of the function lies below the line segment joining any two points of the graph. Equivalently, a function is convex if its epigraph is a convex set...
of t. A metric space is then locally convex if every point has a neighborhood that is convex in this sense. The Cartan–Hadamard theorem for locally convex spaces states:
- If X is a locally convex complete connected metric space, then the universal cover of X is a convex geodesic space with respect to the induced length metricIntrinsic metricIn the mathematical study of metric spaces, one can consider the arclength of paths in the space. If two points are a given distance from each other, it is natural to expect that one should be able to get from one point to another along a path whose arclength is equal to that distance...
d.
In particular, the universal covering of such a space is contractible. The convexity of the distance function along a pair of geodesics is a well-known consequence of non-positive curvature of a metric space, but it is not equivalent .
Significance
The Cartan–Hadamard theorem provides an example of a local-to-global correspondence in Riemannian and metric geometry: namely, a local condition (non-positive curvature) and a global condition (simple-connectedness) together imply a strong global property (contractibility); or in the Riemannian case, diffeomorphism with Rn.The metric form of the theorem demonstrates that a non-positively curved polyhedral cell complex is aspherical
Aspherical space
In topology, a branch of mathematics, an aspherical space is a topological space with all higher homotopy groups equal to 0.If one works with CW complexes, one can reformulate this condition: an aspherical CW complex is a CW complex whose universal cover is contractible. Indeed, contractibility of...
. This fact is of crucial importance for modern geometric group theory
Geometric group theory
Geometric group theory is an area in mathematics devoted to the study of finitely generated groups via exploring the connections between algebraic properties of such groups and topological and geometric properties of spaces on which these groups act .Another important...
.