
Carmichael function
Encyclopedia
In number theory
, the Carmichael
function of a positive integer n, denoted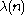 , is defined as the smallest positive integer m such that
, is defined as the smallest positive integer m such that
for every integer a that is coprime
to n. In other words, in more algebraic terms, it defines the exponent of the multiplicative group of integers modulo n
. The Carmichael function is also known as the reduced totient function or the least universal exponent function, and is sometimes also denoted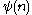 .
.
The first 26 values of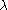 compared to Euler's totient function
compared to Euler's totient function
 :
:
(5,6)=1. Here we had to raise 5 to the 2nd power because the Carmichael function of 6 is 2. Recall that 1 and 5 are the only two numbers smaller than 6 that are relatively prime to 6.
However, 32 = 9 ≡ 3 (mod 6) obviously doesn't work because the number 3 is impermissible as a base to be raised to the 2nd power. We know that gcd(3,6)=3, not 1.
For prime p and positive integer k such that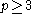 or
or 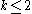 :
: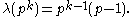 (This is equal to Euler's totient function
(This is equal to Euler's totient function
,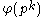 )
)
For ,
,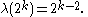
For distinct primes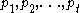 and positive integers
and positive integers  :
:
where denotes the least common multiple
denotes the least common multiple
.
Carmichael's theorem states that if a is coprime
to n, then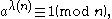
where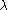 is the Carmichael function defined recursively. In other words, it asserts the correctness of the recursion. This can be proven by considering any primitive root modulo n
is the Carmichael function defined recursively. In other words, it asserts the correctness of the recursion. This can be proven by considering any primitive root modulo n
and the Chinese remainder theorem
.
. In fact Carmichael's theorem is related to Euler's theorem, because the exponent of a finite abelian group must divide the order of the group, by elementary group theory. The two functions differ already in small cases: λ(15) = 4 while φ(15) = 8 (see for the associated n).
Fermat's little theorem
is the special case of Euler's theorem in which n is a prime number p. Carmichael's theorem for a prime p adds nothing to Fermat's theorem, because the group in question is a cyclic group
for which the order and exponent are both p − 1.
 and
and  it holds
it holds .
.
This is an immediate consequence of the recursive definition of the Carmichael function.
 and
and  be coprime and
be coprime and
let be the smallest exponent with
be the smallest exponent with  ,
,
then it holds .
.
That is, the orders of primitive roots of unity in the ring of integers modulo are divisors of
are divisors of  .
.
 .
.
For all numbers N and all except o(N) positive integers n ≤ N:
where A is a constant, A ≈ 0.226969.
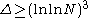 , there are at most
, there are at most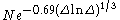
positive integers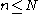 such that
such that 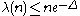 .
.
For any sequence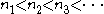 of positive integers, any constant
of positive integers, any constant 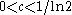 , and any sufficiently large i:
, and any sufficiently large i: .
.
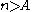 such that
such that 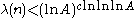 .
.
Moreover, n is of the form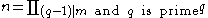
for some square-free integer .
.
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
, the Carmichael
Robert Daniel Carmichael
Robert Daniel Carmichael was a leading American mathematician. Carmichael was born in Goodwater, Alabama. He attended Lineville College, briefly, and he earned his bachelor's degree in 1898, while he was studying towards his Ph.D. degree at Princeton University. Carmichael completed the...
function of a positive integer n, denoted
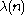 , is defined as the smallest positive integer m such that
, is defined as the smallest positive integer m such that
for every integer a that is coprime
Coprime
In number theory, a branch of mathematics, two integers a and b are said to be coprime or relatively prime if the only positive integer that evenly divides both of them is 1. This is the same thing as their greatest common divisor being 1...
to n. In other words, in more algebraic terms, it defines the exponent of the multiplicative group of integers modulo n
Multiplicative group of integers modulo n
In modular arithmetic the set of congruence classes relatively prime to the modulus n form a group under multiplication called the multiplicative group of integers modulo n. It is also called the group of primitive residue classes modulo n. In the theory of rings, a branch of abstract algebra, it...
. The Carmichael function is also known as the reduced totient function or the least universal exponent function, and is sometimes also denoted
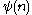 .
.The first 26 values of
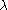 compared to Euler's totient function
compared to Euler's totient functionEuler's totient function
In number theory, the totient \varphi of a positive integer n is defined to be the number of positive integers less than or equal to n that are coprime to n In number theory, the totient \varphi(n) of a positive integer n is defined to be the number of positive integers less than or equal to n that...
 :
:| n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
 |
1 | 1 | 2 | 2 | 4 | 2 | 6 | 2 | 6 | 4 | 10 | 2 | 12 | 6 | 4 | 4 | 16 | 6 | 18 | 4 | 6 | 10 | 22 | 2 | 20 | 12 |
 |
1 | 1 | 2 | 2 | 4 | 2 | 6 | 4 | 6 | 4 | 10 | 4 | 12 | 6 | 8 | 8 | 16 | 6 | 18 | 8 | 12 | 10 | 22 | 8 | 20 | 12 |
Numeric example
52 ≡ 1 (mod 6) because 5 and 6 are coprime. In other words, gcdGreatest common divisor
In mathematics, the greatest common divisor , also known as the greatest common factor , or highest common factor , of two or more non-zero integers, is the largest positive integer that divides the numbers without a remainder.For example, the GCD of 8 and 12 is 4.This notion can be extended to...
(5,6)=1. Here we had to raise 5 to the 2nd power because the Carmichael function of 6 is 2. Recall that 1 and 5 are the only two numbers smaller than 6 that are relatively prime to 6.
However, 32 = 9 ≡ 3 (mod 6) obviously doesn't work because the number 3 is impermissible as a base to be raised to the 2nd power. We know that gcd(3,6)=3, not 1.
Carmichael's theorem
This function can also be defined recursively, as follows.For prime p and positive integer k such that
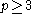 or
or 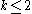 :
: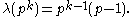 (This is equal to Euler's totient function
(This is equal to Euler's totient functionEuler's totient function
In number theory, the totient \varphi of a positive integer n is defined to be the number of positive integers less than or equal to n that are coprime to n In number theory, the totient \varphi(n) of a positive integer n is defined to be the number of positive integers less than or equal to n that...
,
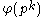 )
)For
 ,
,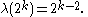
For distinct primes
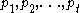 and positive integers
and positive integers  :
:
where
 denotes the least common multiple
denotes the least common multipleLeast common multiple
In arithmetic and number theory, the least common multiple of two integers a and b, usually denoted by LCM, is the smallest positive integer that is a multiple of both a and b...
.
Carmichael's theorem states that if a is coprime
Coprime
In number theory, a branch of mathematics, two integers a and b are said to be coprime or relatively prime if the only positive integer that evenly divides both of them is 1. This is the same thing as their greatest common divisor being 1...
to n, then
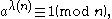
where
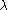 is the Carmichael function defined recursively. In other words, it asserts the correctness of the recursion. This can be proven by considering any primitive root modulo n
is the Carmichael function defined recursively. In other words, it asserts the correctness of the recursion. This can be proven by considering any primitive root modulo nPrimitive root modulo n
In modular arithmetic, a branch of number theory, a primitive root modulo n is any number g with the property that any number coprime to n is congruent to a power of g modulo n. In other words, g is a generator of the multiplicative group of integers modulo n...
and the Chinese remainder theorem
Chinese remainder theorem
The Chinese remainder theorem is a result about congruences in number theory and its generalizations in abstract algebra.In its most basic form it concerned with determining n, given the remainders generated by division of n by several numbers...
.
Hierarchy of results
The classical Euler's theorem implies that λ(n) divides φ(n), Euler's totient functionEuler's totient function
In number theory, the totient \varphi of a positive integer n is defined to be the number of positive integers less than or equal to n that are coprime to n In number theory, the totient \varphi(n) of a positive integer n is defined to be the number of positive integers less than or equal to n that...
. In fact Carmichael's theorem is related to Euler's theorem, because the exponent of a finite abelian group must divide the order of the group, by elementary group theory. The two functions differ already in small cases: λ(15) = 4 while φ(15) = 8 (see for the associated n).
Fermat's little theorem
Fermat's little theorem
Fermat's little theorem states that if p is a prime number, then for any integer a, a p − a will be evenly divisible by p...
is the special case of Euler's theorem in which n is a prime number p. Carmichael's theorem for a prime p adds nothing to Fermat's theorem, because the group in question is a cyclic group
Cyclic group
In group theory, a cyclic group is a group that can be generated by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g .-Definition:A group G is called cyclic if there exists an element g...
for which the order and exponent are both p − 1.
Composition
For all positive integers and
and  it holds
it holds .
.This is an immediate consequence of the recursive definition of the Carmichael function.
Primitive m-th roots of unity
Let and
and  be coprime and
be coprime andlet
 be the smallest exponent with
be the smallest exponent with  ,
,then it holds
 .
.That is, the orders of primitive roots of unity in the ring of integers modulo
 are divisors of
are divisors of  .
.Average and typical value
For any x > 16, and a constant B ≈ 0.34537: .
.For all numbers N and all except o(N) positive integers n ≤ N:

where A is a constant, A ≈ 0.226969.
Lower bounds
For any sufficiently large number N and for any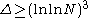 , there are at most
, there are at most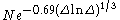
positive integers
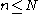 such that
such that 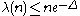 .
.For any sequence
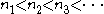 of positive integers, any constant
of positive integers, any constant 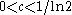 , and any sufficiently large i:
, and any sufficiently large i: .
.Small values
For a constant c and any sufficiently large positive A, there exists an integer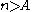 such that
such that 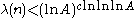 .
.Moreover, n is of the form
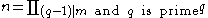
for some square-free integer
 .
.

