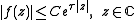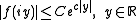Carlson's theorem
Encyclopedia
In mathematics
, in the area of complex analysis
, Carlson's theorem is a uniqueness theorem
about a summable expansion of an analytic function
. It is typically invoked to defend the uniqueness of a Newton series expansion. Carlson's theorem has generalized analogues for expansions in other bases of polynomials. It is named in honour of Fritz David Carlson
.
The theorem may be obtained from the Phragmén–Lindelöf theorem, which is itself an extension of the maximum-modulus theorem.
is an entire function
of exponential type, meaning that
vanishes identically on the non-negative integers.
Then is identically zero.
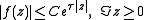
for some
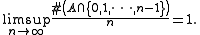
This condition is sharp, meaning that the theorem fails for sets of upper density smaller than 1.
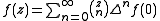
is a Newton series, so that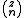 is the binomial coefficient
is the binomial coefficient
and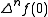 is the n 'th forward difference. Carlson's theorem then states that if all
is the n 'th forward difference. Carlson's theorem then states that if all 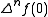 vanish, then
vanish, then 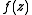 is identically zero. As a trivial corollary, if a Newton series for f exists, and satisfies the Carlson conditions, then f is unique.
is identically zero. As a trivial corollary, if a Newton series for f exists, and satisfies the Carlson conditions, then f is unique.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, in the area of complex analysis
Complex analysis
Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is useful in many branches of mathematics, including number theory and applied mathematics; as well as in physics,...
, Carlson's theorem is a uniqueness theorem
Uniqueness theorem
The uniqueness theorem for Poisson's equation states that the equation has a unique gradient of the solution for a large class of boundary conditions...
about a summable expansion of an analytic function
Analytic function
In mathematics, an analytic function is a function that is locally given by a convergent power series. There exist both real analytic functions and complex analytic functions, categories that are similar in some ways, but different in others...
. It is typically invoked to defend the uniqueness of a Newton series expansion. Carlson's theorem has generalized analogues for expansions in other bases of polynomials. It is named in honour of Fritz David Carlson
Fritz Carlson
Fritz David Carlson was a Swedish mathematician. He's famous for* Carlson's theorem in complex analysis* Carlson's inequality*Carlson–Levin constant*Carlson theorem on Dirichlet series...
.
The theorem may be obtained from the Phragmén–Lindelöf theorem, which is itself an extension of the maximum-modulus theorem.
Statement of theorem
Assume thatis an entire function
Entire function
In complex analysis, an entire function, also called an integral function, is a complex-valued function that is holomorphic over the whole complex plane...
of exponential type, meaning that
- for some
- There exists such that
vanishes identically on the non-negative integers.
Then is identically zero.
First condition
The first condition may be relaxed: it is enough to assume that is analytic in , continuous in , and satisfies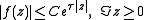
for some
Second condition
To see that the second condition is sharp, consider the function = . It vanishes on the integers; however, it grows exponentially on the imaginary axis with a growth rate of = , and indeed it is not identically zero.Third condition
A result, due to , relaxes the condition that vanish on the integers. Namely, Rubel showed that the conclusion of the theorem remains valid if vanishes on a subset } of upper density 1, meaning that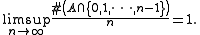
This condition is sharp, meaning that the theorem fails for sets of upper density smaller than 1.
Applications
Suppose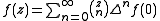
is a Newton series, so that
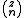 is the binomial coefficient
is the binomial coefficientBinomial coefficient
In mathematics, binomial coefficients are a family of positive integers that occur as coefficients in the binomial theorem. They are indexed by two nonnegative integers; the binomial coefficient indexed by n and k is usually written \tbinom nk , and it is the coefficient of the x k term in...
and
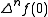 is the n 'th forward difference. Carlson's theorem then states that if all
is the n 'th forward difference. Carlson's theorem then states that if all 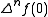 vanish, then
vanish, then 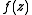 is identically zero. As a trivial corollary, if a Newton series for f exists, and satisfies the Carlson conditions, then f is unique.
is identically zero. As a trivial corollary, if a Newton series for f exists, and satisfies the Carlson conditions, then f is unique.