
Burnside's lemma
Encyclopedia
Burnside's lemma, sometimes also called Burnside's counting theorem, the Cauchy-Frobenius lemma or the orbit-counting theorem, is a result in group theory
which is often useful in taking account of symmetry
when counting mathematical objects. Its various eponyms include William Burnside
, George Pólya
, Augustin Louis Cauchy
, and Ferdinand Georg Frobenius
. The result is not due to Burnside himself, who merely quotes it in his book 'On the Theory of Groups of Finite Order', attributing it instead to .
In the following, let G be a finite group
that acts
on a set X. For each g in G let Xg denote the set of elements in X that are fixed by
g. Burnside's lemma asserts the following formula for the number of orbits, denoted |X/G|:
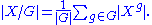
Thus the number of orbits (a natural number
or +∞
) is equal to the average
number of points fixed
by an element of G (which consequently is also a natural number or infinity). If G is infinite, the division by |G| may not be well-defined; in this case the following statement in cardinal arithmetic holds:

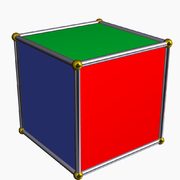
Let X be the set of 36 possible face colour combinations that can be applied to a cube in one particular orientation, and let the rotation group G of the cube act on X in the natural manner. Then two elements of X belong to the same orbit precisely when one is simply a rotation of the other. The number of rotationally distinct colourings is thus the same as the number of orbits and can be found by counting the sizes of the fixed sets for the 24 elements of G.
A detailed examination of these automorphisms may be found
Group theory
In mathematics and abstract algebra, group theory studies the algebraic structures known as groups.The concept of a group is central to abstract algebra: other well-known algebraic structures, such as rings, fields, and vector spaces can all be seen as groups endowed with additional operations and...
which is often useful in taking account of symmetry
Symmetry
Symmetry generally conveys two primary meanings. The first is an imprecise sense of harmonious or aesthetically pleasing proportionality and balance; such that it reflects beauty or perfection...
when counting mathematical objects. Its various eponyms include William Burnside
William Burnside
William Burnside was an English mathematician. He is known mostly as an early contributor to the theory of finite groups....
, George Pólya
George Pólya
George Pólya was a Hungarian mathematician. He was a professor of mathematics from 1914 to 1940 at ETH Zürich and from 1940 to 1953 at Stanford University. He made fundamental contributions to combinatorics, number theory, numerical analysis and probability theory...
, Augustin Louis Cauchy
Augustin Louis Cauchy
Baron Augustin-Louis Cauchy was a French mathematician who was an early pioneer of analysis. He started the project of formulating and proving the theorems of infinitesimal calculus in a rigorous manner, rejecting the heuristic principle of the generality of algebra exploited by earlier authors...
, and Ferdinand Georg Frobenius
Ferdinand Georg Frobenius
Ferdinand Georg Frobenius was a German mathematician, best known for his contributions to the theory of differential equations and to group theory...
. The result is not due to Burnside himself, who merely quotes it in his book 'On the Theory of Groups of Finite Order', attributing it instead to .
In the following, let G be a finite group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
that acts
Group action
In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
on a set X. For each g in G let Xg denote the set of elements in X that are fixed by
Fixed point (mathematics)
In mathematics, a fixed point of a function is a point that is mapped to itself by the function. A set of fixed points is sometimes called a fixed set...
g. Burnside's lemma asserts the following formula for the number of orbits, denoted |X/G|:
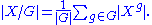
Thus the number of orbits (a natural number
Natural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
or +∞
Extended real number line
In mathematics, the affinely extended real number system is obtained from the real number system R by adding two elements: +∞ and −∞ . The projective extended real number system adds a single object, ∞ and makes no distinction between "positive" or "negative" infinity...
) is equal to the average
Mean
In statistics, mean has two related meanings:* the arithmetic mean .* the expected value of a random variable, which is also called the population mean....
number of points fixed
Fixed point (mathematics)
In mathematics, a fixed point of a function is a point that is mapped to itself by the function. A set of fixed points is sometimes called a fixed set...
by an element of G (which consequently is also a natural number or infinity). If G is infinite, the division by |G| may not be well-defined; in this case the following statement in cardinal arithmetic holds:

Example application
The number of rotationally distinct colourings of the faces of a cube using three colours can be determined from this formula as follows.Let X be the set of 36 possible face colour combinations that can be applied to a cube in one particular orientation, and let the rotation group G of the cube act on X in the natural manner. Then two elements of X belong to the same orbit precisely when one is simply a rotation of the other. The number of rotationally distinct colourings is thus the same as the number of orbits and can be found by counting the sizes of the fixed sets for the 24 elements of G.

- one identity element which leaves all 36 elements of X unchanged
- six 90-degree face rotations, each of which leaves 33 of the elements of X unchanged
- three 180-degree face rotations, each of which leaves 34 of the elements of X unchanged
- eight 120-degree vertex rotations, each of which leaves 32 of the elements of X unchanged
- six 180-degree edge rotations, each of which leaves 33 of the elements of X unchanged
A detailed examination of these automorphisms may be found

