All Topics  
Brillouin zone

 

 
   Email Print
   Bookmark   Link
 

 

Brillouin zone
 
 
  Topics Brillouin zone Topic Home

In mathematics
Mathematics

Mathematics is the study of quantity, structure, space, change, and related topics of pattern and form. Mathematicians seek out patterns whether found in numbers, space, natural science, computers, imaginary abstractions, or elsewhere....
 and solid state physics, the first Brillouin zone is a uniquely defined primitive cell
Primitive cell

In geometry, solid state physics and mineralogy, particularly in describing crystal structure, a primitive cell, is a minimum cell corresponding to a single lattice point of a structure with translational symmetry in 2D, 3D, or other dimensions....
 of the reciprocal lattice
Reciprocal lattice

In crystallography, the Multiplicative inverse lattice of a Bravais lattice is the set of all vector s K such thatfor all lattice point position vectors R....
 in the frequency domain
Frequency domain

In electronics and control systems engineering, frequency domain is a term used to describe the analysis of mathematical functions or Signal with respect to frequency, rather than time....
. It is found by the same method as for the Wigner-Seitz cell
Wigner-Seitz cell

The Wigner-Seitz cell is a geometrical construction which helps in the study of crystalline material in solid-state physics. The unique property of a crystal is that its atoms are arranged in a regular, 3-dimensional array, which is called a Lattice ....
 in the Bravais lattice
Bravais lattice

In geometry and crystallography, a Bravais lattice, named after Auguste Bravais, is an infinite set of points generated by a set of discrete translation operations....
. The importance of the Brillouin zone stems from the Bloch wave
Bloch wave

A Bloch wave or Bloch state, named after Felix Bloch, is the wavefunction of a particle placed in a Particle in a one-dimensional lattice ....
 description of waves in a periodic medium, in which it is found that the solutions can be completely characterized by their behavior in a single Brillouin zone.

Taking surfaces at the same distance from one element of the lattice and its neighbours, the volume
Volume

The volume of any solid, liquid, plasma, vacuum or theoretical object is how much three-dimensional space it occupies, often quantified numerically....
 included is the first Brillouin zone.






Discussion
Ask a question about 'Brillouin zone'
Start a new discussion about 'Brillouin zone'
Answer questions from other users
Full Discussion Forum



Encyclopedia


In mathematics
Mathematics

Mathematics is the study of quantity, structure, space, change, and related topics of pattern and form. Mathematicians seek out patterns whether found in numbers, space, natural science, computers, imaginary abstractions, or elsewhere....
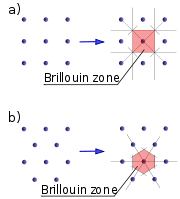
 and solid state physics, the first Brillouin zone is a uniquely defined primitive cell
Primitive cell

In geometry, solid state physics and mineralogy, particularly in describing crystal structure, a primitive cell, is a minimum cell corresponding to a single lattice point of a structure with translational symmetry in 2D, 3D, or other dimensions....
 of the reciprocal lattice
Reciprocal lattice

In crystallography, the Multiplicative inverse lattice of a Bravais lattice is the set of all vector s K such thatfor all lattice point position vectors R....
 in the frequency domain
Frequency domain

In electronics and control systems engineering, frequency domain is a term used to describe the analysis of mathematical functions or Signal with respect to frequency, rather than time....
. It is found by the same method as for the Wigner-Seitz cell
Wigner-Seitz cell

The Wigner-Seitz cell is a geometrical construction which helps in the study of crystalline material in solid-state physics. The unique property of a crystal is that its atoms are arranged in a regular, 3-dimensional array, which is called a Lattice ....
 in the Bravais lattice
Bravais lattice

In geometry and crystallography, a Bravais lattice, named after Auguste Bravais, is an infinite set of points generated by a set of discrete translation operations....
. The importance of the Brillouin zone stems from the Bloch wave
Bloch wave

A Bloch wave or Bloch state, named after Felix Bloch, is the wavefunction of a particle placed in a Particle in a one-dimensional lattice ....
 description of waves in a periodic medium, in which it is found that the solutions can be completely characterized by their behavior in a single Brillouin zone.

Taking surfaces at the same distance from one element of the lattice and its neighbours, the volume
Volume

The volume of any solid, liquid, plasma, vacuum or theoretical object is how much three-dimensional space it occupies, often quantified numerically....
 included is the first Brillouin zone. Another definition is as the set of points in k-space that can be reached from the origin without crossing any Bragg plane
Bragg's law

In physics, Bragg's law is the result of experiments into the diffraction of X-rays or neutron diffraction off crystal surfaces at certain angles, derived by physicist William Lawrence Bragg in 1912 and first presented on 1912-11-11 to the Cambridge Philosophical Society....
. Equivalently, this is the Voronoi cell around the origin of the reciprocal lattice.

There are also second, third, etc., Brillouin zones, corresponding to a sequence of disjoint regions (all with the same volume) at increasing distances from the origin, but these are used more rarely. As a result, the first Brillouin zone is often called simply the Brillouin zone. (In general, the n-th Brillouin zone consist of the set of points that can be reached from the origin by crossing n − 1 Bragg planes.)

A related concept is that of the irreducible Brillouin zone, which is the first Brillouin zone reduced by all of the symmetries in the point group
Point group

In mathematics, a point group is a group of geometric symmetry leaving a point fixed....
 of the lattice.

The concept of a Brillouin zone was developed by Leon Brillouin
Léon Brillouin

L?on Nicolas Brillouin was a France physicist. He was born in S?vres , France. His father, Marcel Brillouin, grand-father, ?leuth?re Mascart, and great-grand-father, Charles Briot, were physicists as well....
 (1889-1969), a French physicist.

Critical points

Several points of high symmetry are of special interest – these are called critical points.
SymbolDescription
GCenter of the Brillouin zone
Simple cube
MCenter of an edge
RCorner point
XCenter of a face
Face-centered cubic
KMiddle of an edge joining two hexagonal faces
LCenter of a hexagonal face
UMiddle of an edge joining a hexagonal and a square face
WCorner point
XCenter of a square face
Body-centered cubic
HCorner point joining four edges
NCenter of a face
PCorner point joining three edges
Hexagonal
ACenter of a hexagonal face
HCorner point
KMiddle of an edge joining two rectangular faces
LMiddle of an edge joining a hexagonal and a rectangular face
MCenter of a rectangular face


See also

  • period lattice
  • fundamental domain
    Fundamental domain

    In geometry, the fundamental domain of a symmetry group of an object or pattern is a part of the pattern, as small as possible, which, based on the symmetry, determines the whole object or pattern....


External links