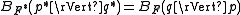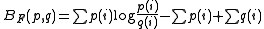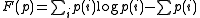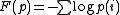Bregman divergence
Encyclopedia
In mathematics
, the Bregman divergence or Bregman distance is similar to a metric
, but does not satisfy the triangle inequality
nor symmetry. There are two ways in which Bregman divergences are important. Firstly, they generalize squared Euclidean distance to a class of distances that all share similar properties. Secondly, they bear a strong connection to exponential families
of distributions; as has been shown by (Banerjee et al. 2005), there is a bijection
between regular exponential families and regular Bregman divergences.
Bregman divergences are named after L. M. Bregman, who introduced the concept in 1967. More recently researchers in geometric algorithms have shown that many important algorithms can be generalized from Euclidean metrics to distances defined by Bregman divergence (Banerjee et al. 2005; Nielsen and Nock 2006; Nielsen et al. 2007).
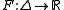 be a continuously-differentiable real-valued and strictly convex function
be a continuously-differentiable real-valued and strictly convex function
defined on a closed convex set
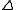 .
.
The Bregman distance associated with F for points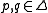 is:
is:
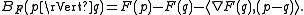
Intuitively, this can be thought of as the difference between the value of F at point p and the value of the first-order Taylor expansion of F around point q evaluated at point p.
is the idea of projective duality, which maps points to hyperplanes and vice versa, while preserving incidence and above-below relationships. There are numerous analytical forms of the projective dual: one common form maps the point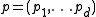 to the hyperplane
to the hyperplane 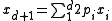 . This mapping can be interpreted (identifying the hyperplane with its normal) as the convex conjugate mapping that takes the point p to its dual point
. This mapping can be interpreted (identifying the hyperplane with its normal) as the convex conjugate mapping that takes the point p to its dual point 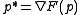 , where F defines the d-dimensional paraboloid
, where F defines the d-dimensional paraboloid 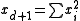 .
.
If we now replace the paraboloid by an arbitrary convex function, we obtain a different dual mapping that retains the incidence and above-below properties of the standard projective dual. This implies that natural dual concepts in computational geometry like Voronoi diagram
s and Delaunay triangulation
s retain their meaning in distance spaces defined by an arbitrary Bregman divergence. Thus, algorithms from "normal" geometry extend directly to these spaces (Nielsen, Nock and Boissonnat, 2006)
. Bregman divergences between functions include total squared error, relative entropy, and squared bias; see the references by Frigyik et al. below for definitions and properties.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Bregman divergence or Bregman distance is similar to a metric
Metric (mathematics)
In mathematics, a metric or distance function is a function which defines a distance between elements of a set. A set with a metric is called a metric space. A metric induces a topology on a set but not all topologies can be generated by a metric...
, but does not satisfy the triangle inequality
Triangle inequality
In mathematics, the triangle inequality states that for any triangle, the sum of the lengths of any two sides must be greater than or equal to the length of the remaining side ....
nor symmetry. There are two ways in which Bregman divergences are important. Firstly, they generalize squared Euclidean distance to a class of distances that all share similar properties. Secondly, they bear a strong connection to exponential families
Exponential family
In probability and statistics, an exponential family is an important class of probability distributions sharing a certain form, specified below. This special form is chosen for mathematical convenience, on account of some useful algebraic properties, as well as for generality, as exponential...
of distributions; as has been shown by (Banerjee et al. 2005), there is a bijection
Bijection
A bijection is a function giving an exact pairing of the elements of two sets. A bijection from the set X to the set Y has an inverse function from Y to X. If X and Y are finite sets, then the existence of a bijection means they have the same number of elements...
between regular exponential families and regular Bregman divergences.
Bregman divergences are named after L. M. Bregman, who introduced the concept in 1967. More recently researchers in geometric algorithms have shown that many important algorithms can be generalized from Euclidean metrics to distances defined by Bregman divergence (Banerjee et al. 2005; Nielsen and Nock 2006; Nielsen et al. 2007).
Definition
Let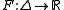 be a continuously-differentiable real-valued and strictly convex function
be a continuously-differentiable real-valued and strictly convex functionConvex function
In mathematics, a real-valued function f defined on an interval is called convex if the graph of the function lies below the line segment joining any two points of the graph. Equivalently, a function is convex if its epigraph is a convex set...
defined on a closed convex set
Convex set
In Euclidean space, an object is convex if for every pair of points within the object, every point on the straight line segment that joins them is also within the object...
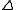 .
.The Bregman distance associated with F for points
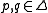 is:
is: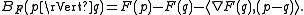
Intuitively, this can be thought of as the difference between the value of F at point p and the value of the first-order Taylor expansion of F around point q evaluated at point p.
Properties
- Non-negativity:
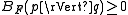 for all p,q. This is a consequence of the convexity of F.
for all p,q. This is a consequence of the convexity of F. - Convexity:
 is convex in its first argument, but not necessarily in the second argument.
is convex in its first argument, but not necessarily in the second argument. - Linearity: If we think of the Bregman distance as an operator on the function F, then it is linear with respect to non-negative coefficients. In other words, for
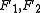 strictly convex and differentiable, and
strictly convex and differentiable, and 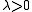 ,
,
-
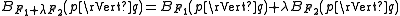
- Duality: The function F has a convex conjugateConvex conjugateIn mathematics, convex conjugation is a generalization of the Legendre transformation. It is also known as Legendre–Fenchel transformation or Fenchel transformation .- Definition :...
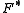 . The Bregman distance defined with respect to
. The Bregman distance defined with respect to 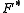 has an interesting relationship to
has an interesting relationship to 
- Duality: The function F has a convex conjugate
- Here,
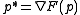 is the dual point corresponding to p
is the dual point corresponding to p
- A key result about Bregman divergences is that, given a random vector, the mean vector minimizes the expected Bregman divergence from the random vector. This result generalizes the textbook result that the mean of a set minimizes total squared error to elements in the set. This result was proved for the vector case by (Banerjee et al. 2005), and extended to the case of functions/distributions by (Frigyik et al. 2008). This result is important because it further justifies using a mean as a representative of a random set, particularly in Bayesian estimation.
Examples
- Squared Euclidean distance
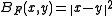 is the canonical example of a Bregman distance, generated by the convex function
is the canonical example of a Bregman distance, generated by the convex function 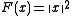
- The squared Mahalanobis distanceMahalanobis distanceIn statistics, Mahalanobis distance is a distance measure introduced by P. C. Mahalanobis in 1936. It is based on correlations between variables by which different patterns can be identified and analyzed. It gauges similarity of an unknown sample set to a known one. It differs from Euclidean...
,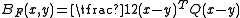 which is generated by the convex function
which is generated by the convex function 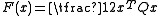 . This can be thought of as a generalization of the above squared Euclidean distance.
. This can be thought of as a generalization of the above squared Euclidean distance.
- The generalized Kullback–Leibler divergenceKullback–Leibler divergenceIn probability theory and information theory, the Kullback–Leibler divergence is a non-symmetric measure of the difference between two probability distributions P and Q...
-
- is generated by the convex function
- The Itakura–Saito distance,
-
- is generated by the convex function
Generalizing projective duality
A key tool in computational geometryComputational geometry
Computational geometry is a branch of computer science devoted to the study of algorithms which can be stated in terms of geometry. Some purely geometrical problems arise out of the study of computational geometric algorithms, and such problems are also considered to be part of computational...
is the idea of projective duality, which maps points to hyperplanes and vice versa, while preserving incidence and above-below relationships. There are numerous analytical forms of the projective dual: one common form maps the point
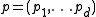 to the hyperplane
to the hyperplane 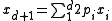 . This mapping can be interpreted (identifying the hyperplane with its normal) as the convex conjugate mapping that takes the point p to its dual point
. This mapping can be interpreted (identifying the hyperplane with its normal) as the convex conjugate mapping that takes the point p to its dual point 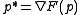 , where F defines the d-dimensional paraboloid
, where F defines the d-dimensional paraboloid 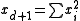 .
.If we now replace the paraboloid by an arbitrary convex function, we obtain a different dual mapping that retains the incidence and above-below properties of the standard projective dual. This implies that natural dual concepts in computational geometry like Voronoi diagram
Voronoi diagram
In mathematics, a Voronoi diagram is a special kind of decomposition of a given space, e.g., a metric space, determined by distances to a specified family of objects in the space...
s and Delaunay triangulation
Delaunay triangulation
In mathematics and computational geometry, a Delaunay triangulation for a set P of points in a plane is a triangulation DT such that no point in P is inside the circumcircle of any triangle in DT. Delaunay triangulations maximize the minimum angle of all the angles of the triangles in the...
s retain their meaning in distance spaces defined by an arbitrary Bregman divergence. Thus, algorithms from "normal" geometry extend directly to these spaces (Nielsen, Nock and Boissonnat, 2006)
Bregman divergences between matrices, functions, distributions
Bregman divergences can also be defined between matrices, between functions, and between measures (distributions). Bregman divergences between matrices include the Stein's loss and von Neumann entropyVon Neumann entropy
In quantum statistical mechanics, von Neumann entropy, named after John von Neumann, is the extension of classical entropy concepts to the field of quantum mechanics....
. Bregman divergences between functions include total squared error, relative entropy, and squared bias; see the references by Frigyik et al. below for definitions and properties.