
Borel summation
Encyclopedia
In mathematics, Borel summation is a summation method for divergent series
, introduced by . There are several variations of this method that are also called Borel summation.
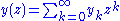
be a formal power series
in z.
Define the Borel transform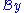 of
of 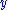 by
by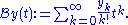
Suppose that the Borel transform converges to an analytic function
near 0 that can be analytically continued
along the positive real axis to a function growing sufficiently slowly that the following integral is well defined (as an improper integral). Then the Borel sum of y is given by
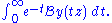
A slightly weaker form of Borel's summation method gives the Borel sum of y as
If the sum exists in this sense then it also exists in the previous sense and is the same, but there are some series that can be summed with the previous method but not with this method .
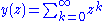
converges to 1/(1-z) for |z|<1. The Borel transform is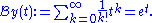
So the Borel sum is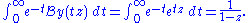
which converges to 1/(1-z) in the larger region Re(z)<1, giving an analytic continuation of the original series.
The series
does not converge for any nonzero z.
The Borel transform is
for |t|<1, and this can be analytically continued to all t≥0.
So the Borel sum is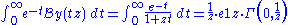 (where Γ is the incomplete Gamma function
(where Γ is the incomplete Gamma function
).
This integral converges for all z≥0, so the original divergent series is Borel summable for all such z. This function has an asymptotic expansion
as z tends to 0 that is given by the original divergent series. This is a typical example of the fact that Borel summation will sometimes "correctly" sum divergent asymptotic expansions.
If y is a power series that converges in some neighborhood of the origin then it has a Borel sum at some point z if it can be analytically continued to a disc with diameter 0z. Conversely if the function can be analytically continued to the disc with diameter 0z then it is Borel summable at z.
The set of points z such that the function can be analytically continued to the interior of the disk with diameter 0z is a polygon when the function has only a finite number of singularities, called the Borel polygon. Its edges pass through the singular points and are orthogonal to lines joining the singular points to 0.
in quantum field theory. In particular in 2-dimensional Euclidean field theory the Schwinger functions can often be recovered from their perturbation series using Borel summation . Some of the singularities of the Borel transform are related to instanton
s and renormalon
s in quantum field theory .
Divergent series
In mathematics, a divergent series is an infinite series that is not convergent, meaning that the infinite sequence of the partial sums of the series does not have a limit....
, introduced by . There are several variations of this method that are also called Borel summation.
Definition
Let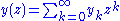
be a formal power series
Formal power series
In mathematics, formal power series are a generalization of polynomials as formal objects, where the number of terms is allowed to be infinite; this implies giving up the possibility to substitute arbitrary values for indeterminates...
in z.
Define the Borel transform
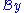 of
of 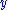 by
by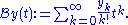
Suppose that the Borel transform converges to an analytic function
Analytic function
In mathematics, an analytic function is a function that is locally given by a convergent power series. There exist both real analytic functions and complex analytic functions, categories that are similar in some ways, but different in others...
near 0 that can be analytically continued
Analytic continuation
In complex analysis, a branch of mathematics, analytic continuation is a technique to extend the domain of a given analytic function. Analytic continuation often succeeds in defining further values of a function, for example in a new region where an infinite series representation in terms of which...
along the positive real axis to a function growing sufficiently slowly that the following integral is well defined (as an improper integral). Then the Borel sum of y is given by
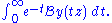
A slightly weaker form of Borel's summation method gives the Borel sum of y as

If the sum exists in this sense then it also exists in the previous sense and is the same, but there are some series that can be summed with the previous method but not with this method .
Examples
The series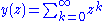
converges to 1/(1-z) for |z|<1. The Borel transform is
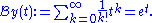
So the Borel sum is
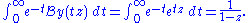
which converges to 1/(1-z) in the larger region Re(z)<1, giving an analytic continuation of the original series.
The series

does not converge for any nonzero z.
The Borel transform is

for |t|<1, and this can be analytically continued to all t≥0.
So the Borel sum is
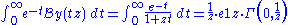 (where Γ is the incomplete Gamma function
(where Γ is the incomplete Gamma functionIncomplete gamma function
In mathematics, the gamma function is defined by a definite integral. The incomplete gamma function is defined as an integral function of the same integrand. There are two varieties of the incomplete gamma function: the upper incomplete gamma function is for the case that the lower limit of...
).
This integral converges for all z≥0, so the original divergent series is Borel summable for all such z. This function has an asymptotic expansion
Asymptotic expansion
In mathematics an asymptotic expansion, asymptotic series or Poincaré expansion is a formal series of functions which has the property that truncating the series after a finite number of terms provides an approximation to a given function as the argument of the function tends towards a particular,...
as z tends to 0 that is given by the original divergent series. This is a typical example of the fact that Borel summation will sometimes "correctly" sum divergent asymptotic expansions.
The Borel polygon
The region where the power series of an analytic function is Borel summable was described as follows by Borel and Phragmen .If y is a power series that converges in some neighborhood of the origin then it has a Borel sum at some point z if it can be analytically continued to a disc with diameter 0z. Conversely if the function can be analytically continued to the disc with diameter 0z then it is Borel summable at z.
The set of points z such that the function can be analytically continued to the interior of the disk with diameter 0z is a polygon when the function has only a finite number of singularities, called the Borel polygon. Its edges pass through the singular points and are orthogonal to lines joining the singular points to 0.
Applications
Borel summation finds application in perturbation expansionsPerturbation theory (quantum mechanics)
In quantum mechanics, perturbation theory is a set of approximation schemes directly related to mathematical perturbation for describing a complicated quantum system in terms of a simpler one. The idea is to start with a simple system for which a mathematical solution is known, and add an...
in quantum field theory. In particular in 2-dimensional Euclidean field theory the Schwinger functions can often be recovered from their perturbation series using Borel summation . Some of the singularities of the Borel transform are related to instanton
Instanton
An instanton is a notion appearing in theoretical and mathematical physics. Mathematically, a Yang–Mills instanton is a self-dual or anti-self-dual connection in a principal bundle over a four-dimensional Riemannian manifold that plays the role of physical space-time in non-abelian gauge theory...
s and renormalon
Renormalon
In quantum field theory, renormalon is a term suggested by 't Hooft to signify a certain type of singularities and contributions. The renormalon singularity is a possible type of singularities arising in the complex Borel plane, as counterpart of instanton singularities...
s in quantum field theory .
See also
- Divergent seriesDivergent seriesIn mathematics, a divergent series is an infinite series that is not convergent, meaning that the infinite sequence of the partial sums of the series does not have a limit....
- Euler summationEuler summationEuler summation is a summability method for convergent and divergent series. Given a series Σan, if its Euler transform converges to a sum, then that sum is called the Euler sum of the original series....
- Cesàro summationCesàro summationIn mathematical analysis, Cesàro summation is an alternative means of assigning a sum to an infinite series. If the series converges in the usual sense to a sum A, then the series is also Cesàro summable and has Cesàro sum A...
- Lambert summationLambert summationIn mathematical analysis, Lambert summation is a summability method for a class of divergent series.-Definition:A series \sum a_n is Lambert summable to A, written \sum a_n = A , if...
- Nachbin resummation
- Abelian and tauberian theoremsAbelian and tauberian theoremsIn mathematics, abelian and tauberian theorems are theorems giving conditions for two methods of summing divergent series to give the same result, named after Niels Henrik Abel and Alfred Tauber...
- Van Wijngaarden transformation

