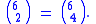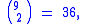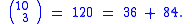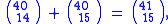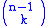Bijective proof
Encyclopedia
In combinatorics
, bijective proof is a proof
technique that finds a bijective function f : A → B between two sets A and B, thus proving that they have the same number of elements, |A| = |B|. One place the technique is useful is where we wish to know the size of A, but can find no direct way of counting its elements. Then establishing a bijection from A to some more easily countable B solves the problem. Another useful feature of the technique is that the nature of the bijection itself often provides powerful insights into each or both of the sets.
Proving the symmetry of the binomial coefficient
The symmetry of the binomial coefficients states that
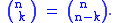
This means there are exactly as many combinations of k in a set of n as there are combinations of n − k in a set of n.
Here is the bijection, i.e. the one-to-one correspondence between the list of all size-2 subsets and the list of all size-4 subsets of the size-6 set whose members are the six letters A, B, C, D, E, F:
Combinatorics
Combinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size , deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria ,...
, bijective proof is a proof
Mathematical proof
In mathematics, a proof is a convincing demonstration that some mathematical statement is necessarily true. Proofs are obtained from deductive reasoning, rather than from inductive or empirical arguments. That is, a proof must demonstrate that a statement is true in all cases, without a single...
technique that finds a bijective function f : A → B between two sets A and B, thus proving that they have the same number of elements, |A| = |B|. One place the technique is useful is where we wish to know the size of A, but can find no direct way of counting its elements. Then establishing a bijection from A to some more easily countable B solves the problem. Another useful feature of the technique is that the nature of the bijection itself often provides powerful insights into each or both of the sets.
Proving the symmetry of the binomial coefficientBinomial coefficientIn mathematics, binomial coefficients are a family of positive integers that occur as coefficients in the binomial theorem. They are indexed by two nonnegative integers; the binomial coefficient indexed by n and k is usually written \tbinom nk , and it is the coefficient of the x k term in...
s
The symmetry of the binomial coefficients states that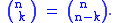
This means there are exactly as many combinations of k in a set of n as there are combinations of n − k in a set of n.
Concrete case: n = 6, k = 2
For example, if n = 6 and k = 2, then n − k = 6 − 2 = 4, so the identity says there are just as many size-2 subsets of a size-6 set as there are size-4 subsets of a size-6 set, i.e.Here is the bijection, i.e. the one-to-one correspondence between the list of all size-2 subsets and the list of all size-4 subsets of the size-6 set whose members are the six letters A, B, C, D, E, F:
-
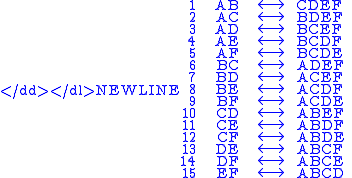
Each size-2 subset corresponds to its complement—the set of all four letters not included in the size-2 subset. Since there are exactly 15 size-2 subsets, there must be exactly 15 size-4 subsets. In mathematical notation,
Similarly, the number of size-6 subsets in a size-20 set must be the same as the number of size-14 subsets in a size-20 set, since 20 − 6 = 14.
The bijective proof
More abstractly and generally, we note that the two quantities asserted to be equal count the subsets of size k and n − k, respectively, of any n-element set S. There is a simple bijection between the two families Fk and Fn − k of subsets of S: it associates every k-element subset with its complementComplement (set theory)In set theory, a complement of a set A refers to things not in , A. The relative complement of A with respect to a set B, is the set of elements in B but not in A...
, which contains precisely the remaining n − k elements of S. Since Fk and Fn − k have the same number of elements, the corresponding binomial coefficients must be equal.
Pascal's triangle
Pascal's triangleIn mathematics, Pascal's triangle is a triangular array of the binomial coefficients in a triangle. It is named after the French mathematician, Blaise Pascal...
recurrence relationRecurrence relationIn mathematics, a recurrence relation is an equation that recursively defines a sequence, once one or more initial terms are given: each further term of the sequence is defined as a function of the preceding terms....
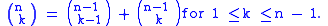
Concrete case: n = 10, k = 3
Rows 9 and 10 of Pascal's trianglePascal's triangleIn mathematics, Pascal's triangle is a triangular array of the binomial coefficients in a triangle. It is named after the French mathematician, Blaise Pascal...
begin as follows:
-

Each number after the initial "1" in row 10 is the sum of the two numbers above it in row 9:
-

and so on. The case 36 + 84 = 120 involves cases 2 and 3 in row 9 and case 3 in row 10 (the rows start with case 0):
Combinatorially, this says:
- The number of ways to choose 2 out of 9
- plus
- the number of ways to choose 3 out of 9
- equals
- the number of ways to choose 3 out of 10.
Here are the 36 ways to choose 2 out of 9 and the 84 ways to choose 3 out of 9:
-
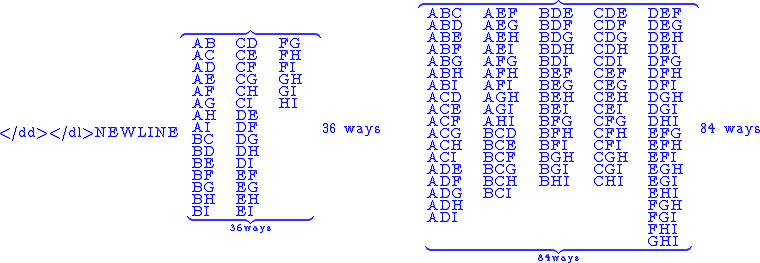
This is a list of 36 + 84 = 120 items. The claim is that this corresponds in one-to-one fashion with the list of all 120 ways to choose 3 out of 10. The nine items used in this example are the first nine letters, A–I of the alphabet. Let the tenth item be the tenth letter, J. Where does J fit into the list of 120 items above? Since we want to build a list of all ways to choose 3 out of 10, and the first 36 items on the list choose 2 out of 9, we simply append J to those items:
-
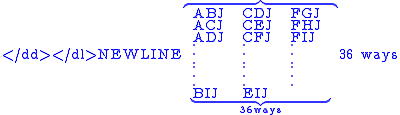
These newly constructed ways to choose 3 items out of 10 can now be counted along with the 84 already-counted ways to choose 3 out of 9, each of which is also a valid way to choose 3 out of 10. The 36 new ways to choose 3 items out of 10 are all valid by construction, and we know we have not missed any new ways, because the tenth item, J, if it is to participate as part of a group of 3, must be joined with 2 other letter, and we already know there are only 36 ways to choose those 2. Thus the number of ways to choose 2 out of 9 plus the number of ways to choose 3 out of 9 is proved to be equal to the number of ways to choose 3 out of 10.
In the same way, the number of ways to choose 14 out of 40 plus the number of ways 15 out of 40 can be shown to be equal to the number of ways to choose 15 out of 41:
and so on.
The bijective proof
Proof.
We count the number of ways to choose k elements from an n-set.
Again, by definition, the left hand side of the equation is the number of ways to choose k from n.
Since 1 ≤ k ≤ n − 1, we can pick a fixed element e from the n-set so that the remaining subset is not empty.
For each k-set, if e is chosen, there are
ways to choose the remaining k − 1 elements among the remaining n − 1 choices; otherwise, there are
ways to choose the remaining k elements among the remaining n − 1 choices. Thus, there are

ways to choose k elements depending on whether e is included in each selection, as in the right hand side expression.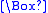
Other examples
Problems that admit combinatorial proofs are not limited to binomial coefficient identities. As the complexity of the problem increases, a combinatorial proof can become very sophisticated. This technique is particularly useful in areas of discrete mathematicsDiscrete mathematicsDiscrete mathematics is the study of mathematical structures that are fundamentally discrete rather than continuous. In contrast to real numbers that have the property of varying "smoothly", the objects studied in discrete mathematics – such as integers, graphs, and statements in logic – do not...
such as combinatoricsCombinatoricsCombinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size , deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria ,...
, graph theoryGraph theoryIn mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
, and number theoryNumber theoryNumber theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
.
The most classical examples of bijective proofs in combinatorics include:- Prüfer sequencePrüfer sequenceIn combinatorial mathematics, the Prüfer sequence of a labeled tree is a unique sequence associated with the tree. The sequence for a tree on n vertices has length n − 2, and can be generated by a simple iterative algorithm...
, giving a proof of Cayley's formula for the number of labeled trees. - Robinson-Schensted algorithmRobinson-Schensted algorithmIn mathematics, the Robinson–Schensted correspondence is a bijective correspondence between permutations and pairs of standard Young tableaux of the same shape. It has various descriptions, all of which are of algorithmic nature, it has many remarkable properties, and it has applications in...
, giving a proof of BurnsideWilliam BurnsideWilliam Burnside was an English mathematician. He is known mostly as an early contributor to the theory of finite groups....
's formula for the symmetric groupSymmetric groupIn mathematics, the symmetric group Sn on a finite set of n symbols is the group whose elements are all the permutations of the n symbols, and whose group operation is the composition of such permutations, which are treated as bijective functions from the set of symbols to itself...
. - Conjugation of Young diagrams, giving a proof of a classical result on the number of certain integer partitionsPartition (number theory)In number theory and combinatorics, a partition of a positive integer n, also called an integer partition, is a way of writing n as a sum of positive integers. Two sums that differ only in the order of their summands are considered to be the same partition; if order matters then the sum becomes a...
. - Bijective proofs of the pentagonal number theorem.
- Bijective proofs of the formula for the Catalan numberCatalan numberIn combinatorial mathematics, the Catalan numbers form a sequence of natural numbers that occur in various counting problems, often involvingrecursively defined objects...
s. - An equivalence between n-vertex directed graphDirected graphA directed graph or digraph is a pair G= of:* a set V, whose elements are called vertices or nodes,...
s (allowing self-loops) and undirected bipartite graphBipartite graphIn the mathematical field of graph theory, a bipartite graph is a graph whose vertices can be divided into two disjoint sets U and V such that every edge connects a vertex in U to one in V; that is, U and V are independent sets...
s with n vertices on each side of the bipartition, induced by viewing the adjacency matrixAdjacency matrixIn mathematics and computer science, an adjacency matrix is a means of representing which vertices of a graph are adjacent to which other vertices...
of the directed graph as a biadjacency matrix of the undirected graph (see bipartite double coverBipartite double coverIn graph theoretic mathematics, the bipartite double cover of an undirected graph G is a bipartite covering graph of G, with twice as many vertices as G. It can be constructed as the tensor product of graphs G × K2...
).
See also
- Cantor–Bernstein–Schroeder theoremCantor–Bernstein–Schroeder theoremIn set theory, the Cantor–Bernstein–Schroeder theorem, named after Georg Cantor, Felix Bernstein, and Ernst Schröder, states that, if there exist injective functions and between the sets A and B, then there exists a bijective function...
- Double counting (proof technique)Double counting (proof technique)In combinatorics, double counting, also called counting in two ways, is a combinatorial proof technique for showing that two expressions are equal by demonstrating that they are two ways of counting the size of one set...
- Combinatorial principlesCombinatorial principlesIn proving results in combinatorics several useful combinatorial rules or combinatorial principles are commonly recognized and used.The rule of sum, rule of product, and inclusion-exclusion principle are often used for enumerative purposes. Bijective proofs are utilized to demonstrate that two sets...
- Combinatorial proofCombinatorial proofIn mathematics, the term combinatorial proof is often used to mean either of two types of proof of an identity in enumerative combinatorics that either states that two sets of combinatorial configurations, depending on one or more parameters, have the same number of elements , or gives a formula...
- Binomial theoremBinomial theoremIn elementary algebra, the binomial theorem describes the algebraic expansion of powers of a binomial. According to the theorem, it is possible to expand the power n into a sum involving terms of the form axbyc, where the exponents b and c are nonnegative integers with , and the coefficient a of...
External links
- "Division by three" – by Doyle and ConwayJohn Horton ConwayJohn Horton Conway is a prolific mathematician active in the theory of finite groups, knot theory, number theory, combinatorial game theory and coding theory...
. - "A direct bijective proof of the hook-length formula" – by Novelli, PakIgor PakIgor Pak is a professor of mathematics at the University of California, Los Angeles, working in combinatorics and discrete probability...
and Stoyanovsky. - "Bijective census and random generation of Eulerian planar maps with prescribed vertex degrees" – by Gilles Schaeffer.
- "Kathy O'Hara's Constructive Proof of the Unimodality of the Gaussian Polynomials" – by Doron ZeilbergerDoron ZeilbergerDoron Zeilberger is an Israeli mathematician, known for his work in combinatorics.He is a Board of Governors Professor of Mathematics at Rutgers University...
. - "Partition Bijections, a Survey" – by Igor PakIgor PakIgor Pak is a professor of mathematics at the University of California, Los Angeles, working in combinatorics and discrete probability...
. - Garsia-Milne Involution Principle – from MathWorldMathWorldMathWorld is an online mathematics reference work, created and largely written by Eric W. Weisstein. It is sponsored by and licensed to Wolfram Research, Inc. and was partially funded by the National Science Foundation's National Science Digital Library grant to the University of Illinois at...
.
-
-
-
-
-