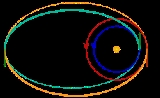
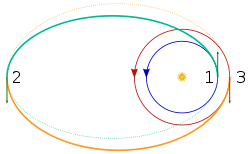
Bi-elliptic transfer
Encyclopedia
In astronautics
and aerospace engineering
, the bi-elliptic transfer is an orbital maneuver
that moves a spacecraft
from one orbit
to another and may, in certain situations, require less delta-v
than a Hohmann transfer
.
The bi-elliptic transfer consists of two half elliptic orbit
s. From the initial orbit, a delta-v is applied boosting the spacecraft into the first transfer orbit with an apoapsis at some point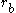 away from the central body
away from the central body
. At this point, a second delta-v is applied sending the spacecraft into the second elliptical orbit with periapsis at the radius of the final desired orbit where a third delta-v is performed injecting the spacecraft into the desired orbit.
While it requires one more burn than a Hohmann transfer and generally requires a greater period of time, the bi-elliptic transfer may require a lower amount of total delta-v than a Hohmann transfer in situations where the ratio of final to the initial semi-major axis
is greater than 11.94
.
The idea of the bi-elliptical transfer trajectory was first published by Ary Sternfeld in 1934.
 Utilizing the vis viva equation
Utilizing the vis viva equation
where,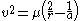
where:
The magnitude
of the first delta-v at the initial circular orbit
with radius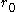 is:
is:
At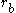 the delta-v is:
the delta-v is: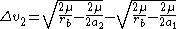
The final delta-v at the final circular orbit with radius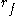 :
: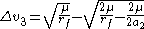
Where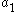 and
and 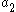 are the semimajor axes of the two elliptical transfer orbits and are given by:
are the semimajor axes of the two elliptical transfer orbits and are given by: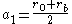
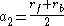
Using the equation for the orbital period
and the notation from above, we have:
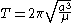
The total transfer time is simply the sum of the time required for each half orbit Therefore we have:
is simply the sum of the time required for each half orbit Therefore we have:

and finally:
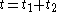
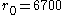 km to a new circular orbit with
km to a new circular orbit with 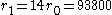 km using Hohmann transfer orbit
km using Hohmann transfer orbit
requires delta-v of 2824.34+1308.38=4132.72 m/s. However if spaceship first accelerates 3060.31 m/s, thus getting in elliptic orbit with apogee at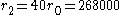 km, then in apogee accelerates another 608.679 m/s, which places it in new orbit with perigee at
km, then in apogee accelerates another 608.679 m/s, which places it in new orbit with perigee at 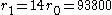 , and, finally, in perigee slows down by 447.554 m/s, placing itself in final circular orbit, then total delta-v will be only 4116.54, which is 16.18 m/s less.
, and, finally, in perigee slows down by 447.554 m/s, placing itself in final circular orbit, then total delta-v will be only 4116.54, which is 16.18 m/s less.
Evidently, the bi-elliptic orbit spends more of its delta-V early on (in the first burn). This yields a higher contribution to the specific orbital energy
and, due to the Oberth effect
, is responsible for the net reduction in required delta-V.
Astronautics
Astronautics, and related astronautical engineering, is the theory and practice of navigation beyond the Earth's atmosphere. In other words, it is the science and technology of space flight....
and aerospace engineering
Aerospace engineering
Aerospace engineering is the primary branch of engineering concerned with the design, construction and science of aircraft and spacecraft. It is divided into two major and overlapping branches: aeronautical engineering and astronautical engineering...
, the bi-elliptic transfer is an orbital maneuver
Orbital maneuver
In spaceflight, an orbital maneuver is the use of propulsion systems to change the orbit of a spacecraft.For spacecraft far from Earth—for example those in orbits around the Sun—an orbital maneuver is called a deep-space maneuver .-delta-v:...
that moves a spacecraft
Spacecraft
A spacecraft or spaceship is a craft or machine designed for spaceflight. Spacecraft are used for a variety of purposes, including communications, earth observation, meteorology, navigation, planetary exploration and transportation of humans and cargo....
from one orbit
Orbit
In physics, an orbit is the gravitationally curved path of an object around a point in space, for example the orbit of a planet around the center of a star system, such as the Solar System...
to another and may, in certain situations, require less delta-v
Delta-v
In astrodynamics a Δv or delta-v is a scalar which takes units of speed. It is a measure of the amount of "effort" that is needed to change from one trajectory to another by making an orbital maneuver....
than a Hohmann transfer
Hohmann transfer orbit
In orbital mechanics, the Hohmann transfer orbit is an elliptical orbit used to transfer between two circular orbits, typically both in the same plane....
.
The bi-elliptic transfer consists of two half elliptic orbit
Elliptic orbit
In astrodynamics or celestial mechanics an elliptic orbit is a Kepler orbit with the eccentricity less than 1; this includes the special case of a circular orbit, with eccentricity equal to zero. In a stricter sense, it is a Kepler orbit with the eccentricity greater than 0 and less than 1 . In a...
s. From the initial orbit, a delta-v is applied boosting the spacecraft into the first transfer orbit with an apoapsis at some point
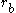 away from the central body
away from the central bodyCentral body
In astrodynamics a central body is a body that is being orbited by an secondary body, or satellite .The central body is properly referred to as the primary body.Under standard assumptions in astrodynamics:...
. At this point, a second delta-v is applied sending the spacecraft into the second elliptical orbit with periapsis at the radius of the final desired orbit where a third delta-v is performed injecting the spacecraft into the desired orbit.
While it requires one more burn than a Hohmann transfer and generally requires a greater period of time, the bi-elliptic transfer may require a lower amount of total delta-v than a Hohmann transfer in situations where the ratio of final to the initial semi-major axis
Semi-major axis
The major axis of an ellipse is its longest diameter, a line that runs through the centre and both foci, its ends being at the widest points of the shape...
is greater than 11.94
.
The idea of the bi-elliptical transfer trajectory was first published by Ary Sternfeld in 1934.
Delta-v

Specific orbital energy
In the gravitational two-body problem, the specific orbital energy \epsilon\,\! of two orbiting bodies is the constant sum of their mutual potential energy and their total kinetic energy , divided by the reduced mass...
where,
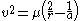
where:
-
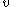 is the speed of an orbiting body
is the speed of an orbiting body  is the standard gravitational parameterStandard gravitational parameterIn astrodynamics, the standard gravitational parameter μ of a celestial body is the product of the gravitational constant G and the mass M of the body.\mu=GM \ The SI units of the standard gravitational parameter are m3s−2....
is the standard gravitational parameterStandard gravitational parameterIn astrodynamics, the standard gravitational parameter μ of a celestial body is the product of the gravitational constant G and the mass M of the body.\mu=GM \ The SI units of the standard gravitational parameter are m3s−2....
of the primary body-
 is the distance of the orbiting body from the primary
is the distance of the orbiting body from the primary -
 is the semi-major axisSemi-major axisThe major axis of an ellipse is its longest diameter, a line that runs through the centre and both foci, its ends being at the widest points of the shape...
is the semi-major axisSemi-major axisThe major axis of an ellipse is its longest diameter, a line that runs through the centre and both foci, its ends being at the widest points of the shape...
of the body's orbit
The magnitude
Magnitude (mathematics)
The magnitude of an object in mathematics is its size: a property by which it can be compared as larger or smaller than other objects of the same kind; in technical terms, an ordering of the class of objects to which it belongs....
of the first delta-v at the initial circular orbit
Circular orbit
A circular orbit is the orbit at a fixed distance around any point by an object rotating around a fixed axis.Below we consider a circular orbit in astrodynamics or celestial mechanics under standard assumptions...
with radius
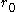 is:
is:
At
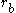 the delta-v is:
the delta-v is: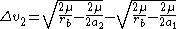
The final delta-v at the final circular orbit with radius
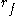 :
: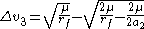
Where
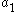 and
and 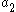 are the semimajor axes of the two elliptical transfer orbits and are given by:
are the semimajor axes of the two elliptical transfer orbits and are given by: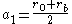
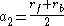
Transfer time
Like the Hohmann transfer, both transfer orbits used in the bi-elliptic transfer constitute exactly one half of an elliptic orbit. This means that the time required to execute each phase of the transfer is simply half the orbital period of each transfer ellipse.Using the equation for the orbital period
Orbital period
The orbital period is the time taken for a given object to make one complete orbit about another object.When mentioned without further qualification in astronomy this refers to the sidereal period of an astronomical object, which is calculated with respect to the stars.There are several kinds of...
and the notation from above, we have:
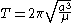
The total transfer time
 is simply the sum of the time required for each half orbit Therefore we have:
is simply the sum of the time required for each half orbit Therefore we have:
and finally:
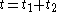
Example
For example, to transfer from circular low earth orbit with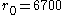 km to a new circular orbit with
km to a new circular orbit with 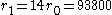 km using Hohmann transfer orbit
km using Hohmann transfer orbitHohmann transfer orbit
In orbital mechanics, the Hohmann transfer orbit is an elliptical orbit used to transfer between two circular orbits, typically both in the same plane....
requires delta-v of 2824.34+1308.38=4132.72 m/s. However if spaceship first accelerates 3060.31 m/s, thus getting in elliptic orbit with apogee at
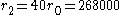 km, then in apogee accelerates another 608.679 m/s, which places it in new orbit with perigee at
km, then in apogee accelerates another 608.679 m/s, which places it in new orbit with perigee at 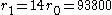 , and, finally, in perigee slows down by 447.554 m/s, placing itself in final circular orbit, then total delta-v will be only 4116.54, which is 16.18 m/s less.
, and, finally, in perigee slows down by 447.554 m/s, placing itself in final circular orbit, then total delta-v will be only 4116.54, which is 16.18 m/s less.| Burn | Hohmann ΔV (m/s) | Bi-elliptic ΔV (m/s) | |
|---|---|---|---|
| 1 | |||
| 2 | |||
| 3 | - | ||
| Total | 4132.72 | 4116.54 |
Evidently, the bi-elliptic orbit spends more of its delta-V early on (in the first burn). This yields a higher contribution to the specific orbital energy
Specific orbital energy
In the gravitational two-body problem, the specific orbital energy \epsilon\,\! of two orbiting bodies is the constant sum of their mutual potential energy and their total kinetic energy , divided by the reduced mass...
and, due to the Oberth effect
Oberth effect
In astronautics, the Oberth effect is where the use of a rocket engine when travelling at high speed generates much more useful energy than one at low speed...
, is responsible for the net reduction in required delta-V.

