Basic introduction to the mathematics of curved spacetime
Encyclopedia
The mathematics of general relativity are very complex. In Newton's
theories of motions, an object's mass and length remain constant as it changes speed, and the rate of passage of time also remains unchanged. As a result, many problems in Newtonian mechanics can be solved with algebra alone. In relativity, on the other hand, mass, length, and the passage of time all change as an object's speed approaches the speed of light. The additional variables greatly complicates calculations of an object's motion. As a result, relativity requires the use of vector
s, tensors, pseudotensor
s, curvilinear coordinates
and many other complex mathematical concepts.
All the mathematics discussed in this article were known before Einstein's
general theory of relativity.
For an introduction based on the specific physical example of particles orbiting a large mass in circular orbit
s, see Newtonian motivations for general relativity
for a nonrelativistic treatment and Theoretical motivation for general relativity
for a fully relativistic treatment.
In mathematics
, physics
, and engineering
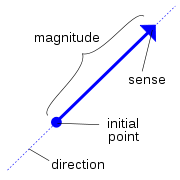
, a Euclidean vector (sometimes called a geometric or spatial vector, or – as here – simply a vector) is a geometric object that has both a magnitude
(or length) and direction. A vector is what is needed to "carry" the point A to the point B; the Latin word vector means "one who carries". The magnitude of the vector is the distance between the two points and the direction refers to the direction of displacement from A to B. Many algebraic operations on real number
s such as addition
, subtraction
, multiplication
, and negation
have close analogues for vectors, operations which obey the familiar algebraic laws of commutativity
, associativity
, and distributivity
.
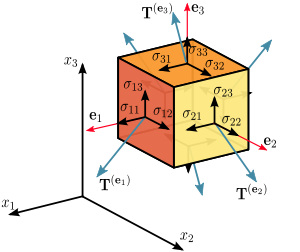A tensor extends the concept of a vector to additional dimensions. A scalar
, that is, a simple set of numbers without direction, would be shown on a graph as a point, a zero-dimensional object. A vector, which has a magnitude and direction, would appear on a graph as a line, which is a one-dimensional object. A tensor extends this concept to additional dimensions. A two dimensional tensor would be called a second order tensor. This can be viewed as a set of related vectors, moving in multiple directions on a plane.
, the magnitude of which is speed
. For example, the velocity 5 meters per second upward could be represented by the vector (0,5) (in 2 dimensions with the positive y axis as 'up'). Another quantity represented by a vector is force
, since it has a magnitude and direction. Vectors also describe many other physical quantities, such as displacement
, acceleration
, momentum
, and angular momentum
. Other physical vectors, such as the electric
and magnetic field
, are represented as a system of vectors at each point of a physical space; that is, a vector field
.
Tensors also have extensive applications in physics:
.
, or list of numbers, which depend on some auxiliary coordinate system or reference frame
. When the coordinates are transformed, for example by rotation or stretching, then the components of the vector also transform. The vector itself has not changed, but the reference frame has, so the components of the vector (or measurements taken with respect to the reference frame) must change to compensate.
The vector is called covariant or contravariant depending on how the transformation of the vector's components is related to the transformation of coordinates.
Coordinate transformation is important because relativity states that there is no one correct reference point in the universe. On earth, we use dimensions like north, east, and elevation, which are used throughout the entire planet. There is no such system for space. Without a clear reference grid, it becomes more accurate to describe the four dimensions as towards/away, left/right, up/down and past/future. As an example event, take the signing of the Declaration of Independence. To a modern observer on Mt Rainier looking East, Revere is ahead, to the right, below, and in the past. However, to an observer in Medieval England looking North, the event is behind, to the left, neither up or down, and in the future. The event itself has not changed, the location of the observer has.
s.
cannot be tensors themselves if the coordinates don't change in a linear way.
Curvilinear coordinates
are coordinates in which the angles between axes can change from point-to-point. This means that rather than having a grid of straight lines, the grid instead has curvature.
A good example of this is the surface of the Earth. While maps frequently portray north, south, east and west as a simple square grid, that is not, in fact, the case. Instead, the longitude lines, running north and south, are curved, and meet at the north pole. This is because the Earth is not flat, but instead round.
In general relativity, gravity has curvature effects on the four dimensions of the universe. A common analogy is placing a heavy object on a stretched out rubber sheet, causing the sheet to bend downward. This curves the coordinate system around the object, much like an object in the universe curves the coordinate system it sits in. The mathematics here are conceptually more complex than on Earth, as it results in 4 dimensions of curved coordinates instead of 3 as used to describe a curved 2D surface.
Isaac Newton
Sir Isaac Newton PRS was an English physicist, mathematician, astronomer, natural philosopher, alchemist, and theologian, who has been "considered by many to be the greatest and most influential scientist who ever lived."...
theories of motions, an object's mass and length remain constant as it changes speed, and the rate of passage of time also remains unchanged. As a result, many problems in Newtonian mechanics can be solved with algebra alone. In relativity, on the other hand, mass, length, and the passage of time all change as an object's speed approaches the speed of light. The additional variables greatly complicates calculations of an object's motion. As a result, relativity requires the use of vector
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
s, tensors, pseudotensor
Pseudotensor
In physics and mathematics, a pseudotensor is usually a quantity that transforms like a tensor under an orientation preserving coordinate transformation , but gains an additional sign flip under an orientation reversing coordinate transformation In physics and mathematics, a pseudotensor is usually...
s, curvilinear coordinates
Curvilinear coordinates
Curvilinear coordinates are a coordinate system for Euclidean space in which the coordinate lines may be curved. These coordinates may be derived from a set of Cartesian coordinates by using a transformation that is locally invertible at each point. This means that one can convert a point given...
and many other complex mathematical concepts.
All the mathematics discussed in this article were known before Einstein's
Albert Einstein
Albert Einstein was a German-born theoretical physicist who developed the theory of general relativity, effecting a revolution in physics. For this achievement, Einstein is often regarded as the father of modern physics and one of the most prolific intellects in human history...
general theory of relativity.
For an introduction based on the specific physical example of particles orbiting a large mass in circular orbit
Circular orbit
A circular orbit is the orbit at a fixed distance around any point by an object rotating around a fixed axis.Below we consider a circular orbit in astrodynamics or celestial mechanics under standard assumptions...
s, see Newtonian motivations for general relativity
Newtonian motivations for general relativity
Some of the basic concepts of General Relativity can be outlined outside the relativistic domain. In particular, the idea that mass/energy generates curvature in space and that curvature affects the motion of masses can be illustrated in a Newtonian setting. We use circular orbits as our prototype....
for a nonrelativistic treatment and Theoretical motivation for general relativity
Theoretical motivation for general relativity
A Theoretical motivation for general relativity, including the motivation for the geodesic equation and the Einstein field equation, can be obtained from special relativity by examining the dynamics of particles in circular orbits about the earth. A key advantage in examining circular orbits is...
for a fully relativistic treatment.
Vectors
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, physics
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
, and engineering
Engineering
Engineering is the discipline, art, skill and profession of acquiring and applying scientific, mathematical, economic, social, and practical knowledge, in order to design and build structures, machines, devices, systems, materials and processes that safely realize improvements to the lives of...
, a Euclidean vector (sometimes called a geometric or spatial vector, or – as here – simply a vector) is a geometric object that has both a magnitude
Magnitude (mathematics)
The magnitude of an object in mathematics is its size: a property by which it can be compared as larger or smaller than other objects of the same kind; in technical terms, an ordering of the class of objects to which it belongs....
(or length) and direction. A vector is what is needed to "carry" the point A to the point B; the Latin word vector means "one who carries". The magnitude of the vector is the distance between the two points and the direction refers to the direction of displacement from A to B. Many algebraic operations on real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s such as addition
Addition
Addition is a mathematical operation that represents combining collections of objects together into a larger collection. It is signified by the plus sign . For example, in the picture on the right, there are 3 + 2 apples—meaning three apples and two other apples—which is the same as five apples....
, subtraction
Subtraction
In arithmetic, subtraction is one of the four basic binary operations; it is the inverse of addition, meaning that if we start with any number and add any number and then subtract the same number we added, we return to the number we started with...
, multiplication
Multiplication
Multiplication is the mathematical operation of scaling one number by another. It is one of the four basic operations in elementary arithmetic ....
, and negation
Negation
In logic and mathematics, negation, also called logical complement, is an operation on propositions, truth values, or semantic values more generally. Intuitively, the negation of a proposition is true when that proposition is false, and vice versa. In classical logic negation is normally identified...
have close analogues for vectors, operations which obey the familiar algebraic laws of commutativity
Commutativity
In mathematics an operation is commutative if changing the order of the operands does not change the end result. It is a fundamental property of many binary operations, and many mathematical proofs depend on it...
, associativity
Associativity
In mathematics, associativity is a property of some binary operations. It means that, within an expression containing two or more occurrences in a row of the same associative operator, the order in which the operations are performed does not matter as long as the sequence of the operands is not...
, and distributivity
Distributivity
In mathematics, and in particular in abstract algebra, distributivity is a property of binary operations that generalizes the distributive law from elementary algebra.For example:...
.
Tensors
Scalar
Scalar may refer to:*Scalar , a quantity used to multiply vectors in the context of vector spaces*Scalar , a quantity which is independent of specific classes of coordinate systems...
, that is, a simple set of numbers without direction, would be shown on a graph as a point, a zero-dimensional object. A vector, which has a magnitude and direction, would appear on a graph as a line, which is a one-dimensional object. A tensor extends this concept to additional dimensions. A two dimensional tensor would be called a second order tensor. This can be viewed as a set of related vectors, moving in multiple directions on a plane.
Applications
Vectors are fundamental in the physical sciences. They can be used to represent any quantity that has both a magnitude and direction, such as velocityVelocity
In physics, velocity is speed in a given direction. Speed describes only how fast an object is moving, whereas velocity gives both the speed and direction of the object's motion. To have a constant velocity, an object must have a constant speed and motion in a constant direction. Constant ...
, the magnitude of which is speed
Speed
In kinematics, the speed of an object is the magnitude of its velocity ; it is thus a scalar quantity. The average speed of an object in an interval of time is the distance traveled by the object divided by the duration of the interval; the instantaneous speed is the limit of the average speed as...
. For example, the velocity 5 meters per second upward could be represented by the vector (0,5) (in 2 dimensions with the positive y axis as 'up'). Another quantity represented by a vector is force
Force
In physics, a force is any influence that causes an object to undergo a change in speed, a change in direction, or a change in shape. In other words, a force is that which can cause an object with mass to change its velocity , i.e., to accelerate, or which can cause a flexible object to deform...
, since it has a magnitude and direction. Vectors also describe many other physical quantities, such as displacement
Displacement (vector)
A displacement is the shortest distance from the initial to the final position of a point P. Thus, it is the length of an imaginary straight path, typically distinct from the path actually travelled by P...
, acceleration
Acceleration
In physics, acceleration is the rate of change of velocity with time. In one dimension, acceleration is the rate at which something speeds up or slows down. However, since velocity is a vector, acceleration describes the rate of change of both the magnitude and the direction of velocity. ...
, momentum
Momentum
In classical mechanics, linear momentum or translational momentum is the product of the mass and velocity of an object...
, and angular momentum
Angular momentum
In physics, angular momentum, moment of momentum, or rotational momentum is a conserved vector quantity that can be used to describe the overall state of a physical system...
. Other physical vectors, such as the electric
Electric field
In physics, an electric field surrounds electrically charged particles and time-varying magnetic fields. The electric field depicts the force exerted on other electrically charged objects by the electrically charged particle the field is surrounding...
and magnetic field
Magnetic field
A magnetic field is a mathematical description of the magnetic influence of electric currents and magnetic materials. The magnetic field at any given point is specified by both a direction and a magnitude ; as such it is a vector field.Technically, a magnetic field is a pseudo vector;...
, are represented as a system of vectors at each point of a physical space; that is, a vector field
Vector field
In vector calculus, a vector field is an assignmentof a vector to each point in a subset of Euclidean space. A vector field in the plane for instance can be visualized as an arrow, with a given magnitude and direction, attached to each point in the plane...
.
Tensors also have extensive applications in physics:
- Electromagnetic tensorElectromagnetic tensorThe electromagnetic tensor or electromagnetic field tensor is a mathematical object that describes the electromagnetic field of a physical system in Maxwell's theory of electromagnetism...
(or Faraday's tensor) in electromagnetismElectromagnetismElectromagnetism is one of the four fundamental interactions in nature. The other three are the strong interaction, the weak interaction and gravitation... - Finite deformation tensorsFinite deformation tensorsIn continuum mechanics, the finite strain theory—also called large strain theory, or large deformation theory—deals with deformations in which both rotations and strains are arbitrarily large, i.e. invalidates the assumptions inherent in infinitesimal strain theory...
for describing deformations and strain tensor for strainStrain (materials science)In continuum mechanics, the infinitesimal strain theory, sometimes called small deformation theory, small displacement theory, or small displacement-gradient theory, deals with infinitesimal deformations of a continuum body...
in continuum mechanicsContinuum mechanicsContinuum mechanics is a branch of mechanics that deals with the analysis of the kinematics and the mechanical behavior of materials modelled as a continuous mass rather than as discrete particles... - PermittivityPermittivityIn electromagnetism, absolute permittivity is the measure of the resistance that is encountered when forming an electric field in a medium. In other words, permittivity is a measure of how an electric field affects, and is affected by, a dielectric medium. The permittivity of a medium describes how...
and electric susceptibilityElectric susceptibilityIn electromagnetism, the electric susceptibility \chi_e is a dimensionless proportionality constant that indicates the degree of polarization of a dielectric material in response to an applied electric field...
are tensors in anisotropic media - Stress-energy tensorStress-energy tensorThe stress–energy tensor is a tensor quantity in physics that describes the density and flux of energy and momentum in spacetime, generalizing the stress tensor of Newtonian physics. It is an attribute of matter, radiation, and non-gravitational force fields...
in general relativityGeneral relativityGeneral relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
, used to represent momentumMomentumIn classical mechanics, linear momentum or translational momentum is the product of the mass and velocity of an object...
fluxFluxIn the various subfields of physics, there exist two common usages of the term flux, both with rigorous mathematical frameworks.* In the study of transport phenomena , flux is defined as flow per unit area, where flow is the movement of some quantity per time...
es - Spherical tensor operators are the eigenfunctions of the quantum angular momentumAngular momentumIn physics, angular momentum, moment of momentum, or rotational momentum is a conserved vector quantity that can be used to describe the overall state of a physical system...
operator in spherical coordinates - Diffusion tensors, the basis of Diffusion Tensor Imaging, represent rates of diffusion in biologic environments
Dimensions
In relativity, four-dimensional vectors, or four-vectors are required. These four dimensions are length, height, width and time. In this context, a point would be an event, as it has both a location and a time. Similar to vectors, tensors require four dimensions. One example is the Riemann curvature tensorRiemann curvature tensor
In the mathematical field of differential geometry, the Riemann curvature tensor, or Riemann–Christoffel tensor after Bernhard Riemann and Elwin Bruno Christoffel, is the most standard way to express curvature of Riemannian manifolds...
.
Coordinate transformation
In physics, as well as mathematics, a vector is often identified with a tupleTuple
In mathematics and computer science, a tuple is an ordered list of elements. In set theory, an n-tuple is a sequence of n elements, where n is a positive integer. There is also one 0-tuple, an empty sequence. An n-tuple is defined inductively using the construction of an ordered pair...
, or list of numbers, which depend on some auxiliary coordinate system or reference frame
Frame of reference
A frame of reference in physics, may refer to a coordinate system or set of axes within which to measure the position, orientation, and other properties of objects in it, or it may refer to an observational reference frame tied to the state of motion of an observer.It may also refer to both an...
. When the coordinates are transformed, for example by rotation or stretching, then the components of the vector also transform. The vector itself has not changed, but the reference frame has, so the components of the vector (or measurements taken with respect to the reference frame) must change to compensate.
The vector is called covariant or contravariant depending on how the transformation of the vector's components is related to the transformation of coordinates.
- Contravariant vectors are "regular vectors" with units of distance (such as a displacement) or distance times some other unit (such as velocity or acceleration). For example, in changing units from meters to millimeters, a displacement of 1 m becomes 1000 mm.
- Covariant vectors, on the other hand, have units of one-over-distance (typically such as gradientGradientIn vector calculus, the gradient of a scalar field is a vector field that points in the direction of the greatest rate of increase of the scalar field, and whose magnitude is the greatest rate of change....
). For example, in changing again from meters to millimeters, a gradient of 1 KKelvinThe kelvin is a unit of measurement for temperature. It is one of the seven base units in the International System of Units and is assigned the unit symbol K. The Kelvin scale is an absolute, thermodynamic temperature scale using as its null point absolute zero, the temperature at which all...
/m becomes 0.001 K/mm.
Coordinate transformation is important because relativity states that there is no one correct reference point in the universe. On earth, we use dimensions like north, east, and elevation, which are used throughout the entire planet. There is no such system for space. Without a clear reference grid, it becomes more accurate to describe the four dimensions as towards/away, left/right, up/down and past/future. As an example event, take the signing of the Declaration of Independence. To a modern observer on Mt Rainier looking East, Revere is ahead, to the right, below, and in the past. However, to an observer in Medieval England looking North, the event is behind, to the left, neither up or down, and in the future. The event itself has not changed, the location of the observer has.
Oblique axes
An oblique coordinate system is one in which the axes are not necessarily orthogonal to each other; that is, they meet at angles other than right angleRight angle
In geometry and trigonometry, a right angle is an angle that bisects the angle formed by two halves of a straight line. More precisely, if a ray is placed so that its endpoint is on a line and the adjacent angles are equal, then they are right angles...
s.
Nontensors
A nontensor is a tensor-like quantity that behaves like a tensor in the raising and lowering of indices, but that does not transform like a tensor under a coordinate transformation. For example, Christoffel symbolsChristoffel symbols
In mathematics and physics, the Christoffel symbols, named for Elwin Bruno Christoffel , are numerical arrays of real numbers that describe, in coordinates, the effects of parallel transport in curved surfaces and, more generally, manifolds. As such, they are coordinate-space expressions for the...
cannot be tensors themselves if the coordinates don't change in a linear way.
Curvilinear coordinates and curved spacetime
Curvilinear coordinates
Curvilinear coordinates are a coordinate system for Euclidean space in which the coordinate lines may be curved. These coordinates may be derived from a set of Cartesian coordinates by using a transformation that is locally invertible at each point. This means that one can convert a point given...
are coordinates in which the angles between axes can change from point-to-point. This means that rather than having a grid of straight lines, the grid instead has curvature.
A good example of this is the surface of the Earth. While maps frequently portray north, south, east and west as a simple square grid, that is not, in fact, the case. Instead, the longitude lines, running north and south, are curved, and meet at the north pole. This is because the Earth is not flat, but instead round.
In general relativity, gravity has curvature effects on the four dimensions of the universe. A common analogy is placing a heavy object on a stretched out rubber sheet, causing the sheet to bend downward. This curves the coordinate system around the object, much like an object in the universe curves the coordinate system it sits in. The mathematics here are conceptually more complex than on Earth, as it results in 4 dimensions of curved coordinates instead of 3 as used to describe a curved 2D surface.
Parallel transport
The relation between neighboring contravariant vectors: Christoffel symbols
The constancy of the length of the parallel displaced vector
From Dirac:The constancy of the length of the vector follows from geometrical arguments. When we split up the vector into tangential and normal parts ... the normal part is infinitesimal and is orthogonal to the tangential part. It follows that, to the first order, the length of the whole vector equals that of its tangential part.
See also
- Differentiable manifoldDifferentiable manifoldA differentiable manifold is a type of manifold that is locally similar enough to a linear space to allow one to do calculus. Any manifold can be described by a collection of charts, also known as an atlas. One may then apply ideas from calculus while working within the individual charts, since...
- Christoffel symbol
- Riemannian geometryRiemannian geometryRiemannian geometry is the branch of differential geometry that studies Riemannian manifolds, smooth manifolds with a Riemannian metric, i.e. with an inner product on the tangent space at each point which varies smoothly from point to point. This gives, in particular, local notions of angle, length...
- Differential geometry and topologyDifferential geometry and topologyDifferential geometry is a mathematical discipline that uses the techniques of differential and integral calculus, as well as linear and multilinear algebra, to study problems in geometry. The theory of plane and space curves and of surfaces in the three-dimensional Euclidean space formed the basis...
- List of differential geometry topics
- General RelativityGeneral relativityGeneral relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
- Gauge gravitation theoryGauge gravitation theoryIn quantum field theory, gauge gravitation theory is the effort to extend Yang–Mills theory, which provides a universal description of the fundamental interactions, to describe gravity.The first gauge model of gravity was...