
Azumaya algebra
Encyclopedia
In mathematics
, an Azumaya algebra is a generalization of central simple algebra
s to R-algebras where R need not be a field
. Such a notion was introduced in a 1951 paper of Goro Azumaya
, for the case where R is a commutative local ring. The notion was developed further in ring theory
, and in algebraic geometry
, where Alexander Grothendieck
made it the basis for his geometric theory of the Brauer group
in Bourbaki seminars from 1964-5. There are now several points of access to the basic definitions.
An Azumaya algebra over a commutative local ring R is an R-algebra A that is free and of finite rank r as an R-module, such that the tensor product
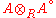 (where Ao is the opposite algebra
(where Ao is the opposite algebra
) is isomorphic to the matrix algebra
EndR(A) ≈ Mr(A) via the map sending to the endomorphism x → axb of A.
to the endomorphism x → axb of A.
An Azumaya algebra on a scheme X with structure sheaf OX, according to the original Grothendieck seminar, is a sheaf A of OX-algebras that is étale locally isomorphic to a matrix algebra sheaf. Milne, Étale Cohomology, starts instead from the definition that it is a sheaf A of OX-algebras whose stalk Ax at each point x is an Azumaya algebra over the local ring
OX,x in the sense given above.
Two Azumaya algebras A1 and A2 are equivalent if there exist finite rank locally free sheaves E1 and E2 such that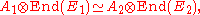
where End(Ei) is the endomorphism sheaf of Ei. The Brauer group of X (an analogue of the Brauer group
of a field) is the set of equivalence classes of Azumaya algebras. The group operation is given by tensor product, and the inverse is given by the opposite algebra.
There have been significant applications of Azumaya algebras in diophantine geometry
, following work of Yuri Manin. The Manin obstruction
to the Hasse principle
is defined using the Brauer group of schemes.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, an Azumaya algebra is a generalization of central simple algebra
Central simple algebra
In ring theory and related areas of mathematics a central simple algebra over a field K is a finite-dimensional associative algebra A, which is simple, and for which the center is exactly K...
s to R-algebras where R need not be a field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
. Such a notion was introduced in a 1951 paper of Goro Azumaya
Goro Azumaya
was a Japanese mathematician who introduced the notion of Azumaya algebra in 1951. His advisor was Shokichi Iyanaga. At the time of his death he was an emeritus professor at Indiana University.-External links:...
, for the case where R is a commutative local ring. The notion was developed further in ring theory
Ring theory
In abstract algebra, ring theory is the study of rings—algebraic structures in which addition and multiplication are defined and have similar properties to those familiar from the integers...
, and in algebraic geometry
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
, where Alexander Grothendieck
Alexander Grothendieck
Alexander Grothendieck is a mathematician and the central figure behind the creation of the modern theory of algebraic geometry. His research program vastly extended the scope of the field, incorporating major elements of commutative algebra, homological algebra, sheaf theory, and category theory...
made it the basis for his geometric theory of the Brauer group
Brauer group
In mathematics, the Brauer group of a field K is an abelian group whose elements are Morita equivalence classes of central simple algebras of finite rank over K and addition is induced by the tensor product of algebras. It arose out of attempts to classify division algebras over a field and is...
in Bourbaki seminars from 1964-5. There are now several points of access to the basic definitions.
An Azumaya algebra over a commutative local ring R is an R-algebra A that is free and of finite rank r as an R-module, such that the tensor product
Tensor product
In mathematics, the tensor product, denoted by ⊗, may be applied in different contexts to vectors, matrices, tensors, vector spaces, algebras, topological vector spaces, and modules, among many other structures or objects. In each case the significance of the symbol is the same: the most general...
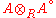 (where Ao is the opposite algebra
(where Ao is the opposite algebraOpposite ring
In algebra, the opposite of a ring is another ring with the same elements and addition operation, but with the multiplication performed in the reverse order....
) is isomorphic to the matrix algebra
Matrix algebra
Matrix algebra may refer to:*Matrix theory, is the branch of mathematics that studies matrices*Matrix ring, thought of as an algebra over a field or a commutative ring...
EndR(A) ≈ Mr(A) via the map sending
 to the endomorphism x → axb of A.
to the endomorphism x → axb of A.An Azumaya algebra on a scheme X with structure sheaf OX, according to the original Grothendieck seminar, is a sheaf A of OX-algebras that is étale locally isomorphic to a matrix algebra sheaf. Milne, Étale Cohomology, starts instead from the definition that it is a sheaf A of OX-algebras whose stalk Ax at each point x is an Azumaya algebra over the local ring
Local ring
In abstract algebra, more particularly in ring theory, local rings are certain rings that are comparatively simple, and serve to describe what is called "local behaviour", in the sense of functions defined on varieties or manifolds, or of algebraic number fields examined at a particular place, or...
OX,x in the sense given above.
Two Azumaya algebras A1 and A2 are equivalent if there exist finite rank locally free sheaves E1 and E2 such that
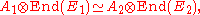
where End(Ei) is the endomorphism sheaf of Ei. The Brauer group of X (an analogue of the Brauer group
Brauer group
In mathematics, the Brauer group of a field K is an abelian group whose elements are Morita equivalence classes of central simple algebras of finite rank over K and addition is induced by the tensor product of algebras. It arose out of attempts to classify division algebras over a field and is...
of a field) is the set of equivalence classes of Azumaya algebras. The group operation is given by tensor product, and the inverse is given by the opposite algebra.
There have been significant applications of Azumaya algebras in diophantine geometry
Diophantine geometry
In mathematics, diophantine geometry is one approach to the theory of Diophantine equations, formulating questions about such equations in terms of algebraic geometry over a ground field K that is not algebraically closed, such as the field of rational numbers or a finite field, or more general...
, following work of Yuri Manin. The Manin obstruction
Manin obstruction
In mathematics, in the field of arithmetic algebraic geometry, the Manin obstruction is attached to a geometric object X which measures the failure of the Hasse principle for X: that is, if the value of the obstruction is non-trivial, then X may have points over all local fields but not over a...
to the Hasse principle
Hasse principle
In mathematics, Helmut Hasse's local-global principle, also known as the Hasse principle, is the idea that one can find an integer solution to an equation by using the Chinese remainder theorem to piece together solutions modulo powers of each different prime number...
is defined using the Brauer group of schemes.

