
Axiom of pairing
Encyclopedia
In axiomatic set theory and the branches of logic
, mathematics
, and computer science
that use it, the axiom of pairing is one of the axiom
s of Zermelo–Fraenkel set theory
.
of the Zermelo–Fraenkel axioms, the axiom reads: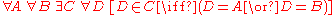
or in words:
or in simpler words:
We can use the axiom of extensionality
to show that this set C is unique.
We call the set C the pair of A and B, and denote it {A,B}.
Thus the essence of the axiom is:
{A,A} is abbreviated {A}, called the singleton containing A.
Note that a singleton is a special case of a pair.
The axiom of pairing also allows for the definition of ordered pairs. For any sets and
and  , the ordered pair
, the ordered pair
is defined by the following:
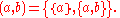
Note that this definition satisfies the condition

Ordered n-tuples
can be defined recursively as follows:
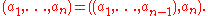
, the axiom of pairing follows from the axiom schema of replacement
applied to any given set with two or more elements, and thus it is sometimes omitted. The existence of such a set with two elements, such as { {}, { {} } }, can be deduced either from the axiom of empty set
and the axiom of power set
or from the axiom of infinity
.
, the axiom of pairing can be generalised to the following schema: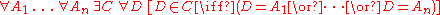
that is:
This set C is again unique by the axiom of extension, and is denoted {A1,...,An}.
Of course, we can't refer to a finite number of sets rigorously without already having in our hands a (finite) set to which the sets in question belong.
Thus, this is not a single statement but instead a schema, with a separate statement for each natural number
n.
For example, to prove the case n = 3, use the axiom of pairing three times, to produce the pair {A1,A2}, the singleton {A3}, and then the pair .
The axiom of union then produces the desired result, {A1,A2,A3}. We can extend this schema to include n=0 if we interpret that case as the axiom of empty set
.
Thus, one may use this as an axiom schema
in the place of the axioms of empty set and pairing. Normally, however, one uses the axioms of empty set and pairing separately, and then proves this as a theorem
schema. Note that adopting this as an axiom schema will not replace the axiom of union
, which is still needed for other situations.
is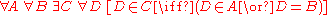 .
.
Using {} for A and x for B, we get {x} for C. Then use {x} for A and y for B, getting {x,y} for C. One may continue in this fashion to build up any finite set. And this could be used to generate all hereditarily finite set
s without using the axiom of union
.
Logic
In philosophy, Logic is the formal systematic study of the principles of valid inference and correct reasoning. Logic is used in most intellectual activities, but is studied primarily in the disciplines of philosophy, mathematics, semantics, and computer science...
, mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, and computer science
Computer science
Computer science or computing science is the study of the theoretical foundations of information and computation and of practical techniques for their implementation and application in computer systems...
that use it, the axiom of pairing is one of the axiom
Axiom
In traditional logic, an axiom or postulate is a proposition that is not proven or demonstrated but considered either to be self-evident or to define and delimit the realm of analysis. In other words, an axiom is a logical statement that is assumed to be true...
s of Zermelo–Fraenkel set theory
Zermelo–Fraenkel set theory
In mathematics, Zermelo–Fraenkel set theory with the axiom of choice, named after mathematicians Ernst Zermelo and Abraham Fraenkel and commonly abbreviated ZFC, is one of several axiomatic systems that were proposed in the early twentieth century to formulate a theory of sets without the paradoxes...
.
Formal statement
In the formal languageFormal language
A formal language is a set of words—that is, finite strings of letters, symbols, or tokens that are defined in the language. The set from which these letters are taken is the alphabet over which the language is defined. A formal language is often defined by means of a formal grammar...
of the Zermelo–Fraenkel axioms, the axiom reads:
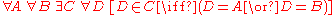
or in words:
- Given any set A and any set B, there isExistential quantificationIn predicate logic, an existential quantification is the predication of a property or relation to at least one member of the domain. It is denoted by the logical operator symbol ∃ , which is called the existential quantifier...
a set C such that, given any set D, D is a member of C if and only ifIf and only ifIn logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
D is equal to A orLogical disjunctionIn logic and mathematics, a two-place logical connective or, is a logical disjunction, also known as inclusive disjunction or alternation, that results in true whenever one or more of its operands are true. E.g. in this context, "A or B" is true if A is true, or if B is true, or if both A and B are...
D is equal to B.
or in simpler words:
- Given two sets, there is a set whose members are exactly the two given sets.
Interpretation
What the axiom is really saying is that, given two sets A and B, we can find a set C whose members are precisely A and B.We can use the axiom of extensionality
Axiom of extensionality
In axiomatic set theory and the branches of logic, mathematics, and computer science that use it, the axiom of extensionality, or axiom of extension, is one of the axioms of Zermelo-Fraenkel set theory.- Formal statement :...
to show that this set C is unique.
We call the set C the pair of A and B, and denote it {A,B}.
Thus the essence of the axiom is:
- Any two sets have a pair.
{A,A} is abbreviated {A}, called the singleton containing A.
Note that a singleton is a special case of a pair.
The axiom of pairing also allows for the definition of ordered pairs. For any sets
 and
and  , the ordered pair
, the ordered pairOrdered pair
In mathematics, an ordered pair is a pair of mathematical objects. In the ordered pair , the object a is called the first entry, and the object b the second entry of the pair...
is defined by the following:
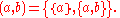
Note that this definition satisfies the condition

Ordered n-tuples
Tuple
In mathematics and computer science, a tuple is an ordered list of elements. In set theory, an n-tuple is a sequence of n elements, where n is a positive integer. There is also one 0-tuple, an empty sequence. An n-tuple is defined inductively using the construction of an ordered pair...
can be defined recursively as follows:
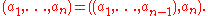
Non-independence
The axiom of pairing is generally considered uncontroversial, and it or an equivalent appears in just about any alternative axiomatization of set theory. Nevertheless, in the standard formulation of the Zermelo–Fraenkel set theoryZermelo–Fraenkel set theory
In mathematics, Zermelo–Fraenkel set theory with the axiom of choice, named after mathematicians Ernst Zermelo and Abraham Fraenkel and commonly abbreviated ZFC, is one of several axiomatic systems that were proposed in the early twentieth century to formulate a theory of sets without the paradoxes...
, the axiom of pairing follows from the axiom schema of replacement
Axiom schema of replacement
In set theory, the axiom schema of replacement is a schema of axioms in Zermelo–Fraenkel set theory that asserts that the image of any set under any definable mapping is also a set...
applied to any given set with two or more elements, and thus it is sometimes omitted. The existence of such a set with two elements, such as { {}, { {} } }, can be deduced either from the axiom of empty set
Axiom of empty set
In axiomatic set theory, the axiom of empty set is an axiom of Zermelo–Fraenkel set theory, the fragment thereof Burgess calls ST, and Kripke–Platek set theory.- Formal statement :...
and the axiom of power set
Axiom of power set
In mathematics, the axiom of power set is one of the Zermelo–Fraenkel axioms of axiomatic set theory.In the formal language of the Zermelo–Fraenkel axioms, the axiom reads:...
or from the axiom of infinity
Axiom of infinity
In axiomatic set theory and the branches of logic, mathematics, and computer science that use it, the axiom of infinity is one of the axioms of Zermelo-Fraenkel set theory...
.
Generalisation
Together with the axiom of empty setAxiom of empty set
In axiomatic set theory, the axiom of empty set is an axiom of Zermelo–Fraenkel set theory, the fragment thereof Burgess calls ST, and Kripke–Platek set theory.- Formal statement :...
, the axiom of pairing can be generalised to the following schema:
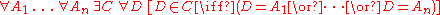
that is:
- Given any finite number of sets A1 through An, there is a set C whose members are precisely A1 through An.
This set C is again unique by the axiom of extension, and is denoted {A1,...,An}.
Of course, we can't refer to a finite number of sets rigorously without already having in our hands a (finite) set to which the sets in question belong.
Thus, this is not a single statement but instead a schema, with a separate statement for each natural number
Natural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
n.
- The case n = 1 is the axiom of pairing with A = A1 and B = A1.
- The case n = 2 is the axiom of pairing with A = A1 and B = A2.
- The cases n > 2 can be proved using the axiom of pairing and the axiom of unionAxiom of unionIn axiomatic set theory and the branches of logic, mathematics, and computer science that use it, the axiom of union is one of the axioms of Zermelo-Fraenkel set theory, stating that, for any set x there is a set y whose elements are precisely the elements of the elements of x...
multiple times.
For example, to prove the case n = 3, use the axiom of pairing three times, to produce the pair {A1,A2}, the singleton {A3}, and then the pair .
The axiom of union then produces the desired result, {A1,A2,A3}. We can extend this schema to include n=0 if we interpret that case as the axiom of empty set
Axiom of empty set
In axiomatic set theory, the axiom of empty set is an axiom of Zermelo–Fraenkel set theory, the fragment thereof Burgess calls ST, and Kripke–Platek set theory.- Formal statement :...
.
Thus, one may use this as an axiom schema
Axiom schema
In mathematical logic, an axiom schema generalizes the notion of axiom.An axiom schema is a formula in the language of an axiomatic system, in which one or more schematic variables appear. These variables, which are metalinguistic constructs, stand for any term or subformula of the system, which...
in the place of the axioms of empty set and pairing. Normally, however, one uses the axioms of empty set and pairing separately, and then proves this as a theorem
Theorem
In mathematics, a theorem is a statement that has been proven on the basis of previously established statements, such as other theorems, and previously accepted statements, such as axioms...
schema. Note that adopting this as an axiom schema will not replace the axiom of union
Axiom of union
In axiomatic set theory and the branches of logic, mathematics, and computer science that use it, the axiom of union is one of the axioms of Zermelo-Fraenkel set theory, stating that, for any set x there is a set y whose elements are precisely the elements of the elements of x...
, which is still needed for other situations.
Another alternative
Another axiom which implies the axiom of pairing in the presence of the axiom of empty setAxiom of empty set
In axiomatic set theory, the axiom of empty set is an axiom of Zermelo–Fraenkel set theory, the fragment thereof Burgess calls ST, and Kripke–Platek set theory.- Formal statement :...
is
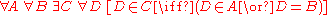 .
.Using {} for A and x for B, we get {x} for C. Then use {x} for A and y for B, getting {x,y} for C. One may continue in this fashion to build up any finite set. And this could be used to generate all hereditarily finite set
Hereditarily finite set
In mathematics and set theory, hereditarily finite sets are defined recursively as finite sets consisting of 0 or more hereditarily finite sets.-Formal definition:...
s without using the axiom of union
Axiom of union
In axiomatic set theory and the branches of logic, mathematics, and computer science that use it, the axiom of union is one of the axioms of Zermelo-Fraenkel set theory, stating that, for any set x there is a set y whose elements are precisely the elements of the elements of x...
.

