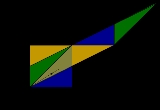
Arnold's cat map
Encyclopedia

Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, Arnold's cat map is a chaotic
Chaos theory
Chaos theory is a field of study in mathematics, with applications in several disciplines including physics, economics, biology, and philosophy. Chaos theory studies the behavior of dynamical systems that are highly sensitive to initial conditions, an effect which is popularly referred to as the...
map from the torus
Torus
In geometry, a torus is a surface of revolution generated by revolving a circle in three dimensional space about an axis coplanar with the circle...
into itself, named after Vladimir Arnold
Vladimir Arnold
Vladimir Igorevich Arnold was a Soviet and Russian mathematician. While he is best known for the Kolmogorov–Arnold–Moser theorem regarding the stability of integrable Hamiltonian systems, he made important contributions in several areas including dynamical systems theory, catastrophe theory,...
, who demonstrated its effects in the 1960s using an image of a cat
Cat
The cat , also known as the domestic cat or housecat to distinguish it from other felids and felines, is a small, usually furry, domesticated, carnivorous mammal that is valued by humans for its companionship and for its ability to hunt vermin and household pests...
, hence the name.
Thinking of the torus
 as the quotient space
as the quotient spaceQuotient space (linear algebra)
In linear algebra, the quotient of a vector space V by a subspace N is a vector space obtained by "collapsing" N to zero. The space obtained is called a quotient space and is denoted V/N ....
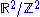 Arnold's cat map is the transformation
Arnold's cat map is the transformation 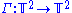 given by the formula
given by the formula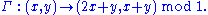
Equivalently, in matrix
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
notation, this is

That is, with a unit size equal to the width of the square image, the image is sheared one unit up, then one unit to the right, and all that lies outside that unit square is shifted back by the unit until it's within the square.
Properties
- Γ is invertible because the matrix has determinantDeterminantIn linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
1 and therefore its inverse has integer entries,
- Γ is area preservingMeasure-preserving dynamical systemIn mathematics, a measure-preserving dynamical system is an object of study in the abstract formulation of dynamical systems, and ergodic theory in particular.-Definition:...
,
- Γ has a unique hyperbolic fixed point (the verticesVertex (geometry)In geometry, a vertex is a special kind of point that describes the corners or intersections of geometric shapes.-Of an angle:...
of the square). The linear transformation which defines the map is hyperbolic: its eigenvalues are irrational numbers, one greater and the other smaller than 1 (in absolute value), so they are associated respectively to an expanding and a contracting eigenspace which are also the stable and unstable manifoldsStable manifoldIn mathematics, and in particular the study of dynamical systems, the idea of stable and unstable sets or stable and unstable manifolds give a formal mathematical definition to the general notions embodied in the idea of an attractor or repellor...
. The eigenspace are orthogonal because the matrix is symmetric. Since the eigenvectors have rationally independentRational dependenceIn mathematics, a collection of real numbers is rationally independent if none of them can be written as a linear combination of the other numbers in the collection with rational coefficients. A collection of numbers which is not rationally independent is called rationally dependent...
components both the eigenspaces denselyDense setIn topology and related areas of mathematics, a subset A of a topological space X is called dense if any point x in X belongs to A or is a limit point of A...
cover the torus. Arnold's cat map is a particularly well-known example of a hyperbolicHyperbolicHyperbolic refers to something related to or in shape of hyperbola , or to something employing the literary device of hyperbole .The following topics are based on the hyperbola etymology:...
toral automorphism, which is an automorphismAutomorphismIn mathematics, an automorphism is an isomorphism from a mathematical object to itself. It is, in some sense, a symmetry of the object, and a way of mapping the object to itself while preserving all of its structure. The set of all automorphisms of an object forms a group, called the automorphism...
of a torusTorusIn geometry, a torus is a surface of revolution generated by revolving a circle in three dimensional space about an axis coplanar with the circle...
given by a square unimodular matrixUnimodular matrixIn mathematics, a unimodular matrix M is a square integer matrix with determinant +1 or −1. Equivalently, it is an integer matrix that is invertible over the integers: there is an integer matrix N which is its inverse...
having no eigenvalues of absolute value 1.
- The set of the points with a periodic orbit is denseDense setIn topology and related areas of mathematics, a subset A of a topological space X is called dense if any point x in X belongs to A or is a limit point of A...
on the torus. Actually a point is preperiodic if and only if its coordinates are rationalRational numberIn mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
.
- Γ is topologically transitive (i.e. there is a point whose orbit is denseDense setIn topology and related areas of mathematics, a subset A of a topological space X is called dense if any point x in X belongs to A or is a limit point of A...
, this happens for example for any points on the expanding eigenspace)
- The number of points with period n is exactly |λ1n + λ2n−2| (where λ1 and λ2 are the eigenvalues of the matrix). For example, the first few terms of this series are 1, 5, 16, 45, 121, 320, 841, 2205 .... (The same equation holds for any unimodular hyperbolic toral automorphism if the eigenvalues are replaced.)
- Γ is ergodic and mixingMixing (physics)In physics, a dynamical system is said to be mixing if the phase space of the system becomes strongly intertwined, according to at least one of several mathematical definitions. For example, a measure-preserving transformation T is said to be strong mixing ifwhenever A and B are any measurable...
,
- Γ is an Anosov diffeomorphismAnosov diffeomorphismIn mathematics, more particularly in the fields of dynamical systems and geometric topology, an Anosov map on a manifold M is a certain type of mapping, from M to itself, with rather clearly marked local directions of 'expansion' and 'contraction'. Anosov systems are a special case of Axiom A...
and in particular it is structurally stableStructural stabilityIn mathematics, structural stability is a fundamental property of a dynamical system which means that the qualitative behavior of the trajectories is unaffected by C1-small perturbations....
.
The discrete cat map

Randomness
Randomness has somewhat differing meanings as used in various fields. It also has common meanings which are connected to the notion of predictability of events....
or disordered, yet after further iterations the image appears to have further order—ghost-like images of the cat, multiple smaller copies arranged in a repeating structure and even upside-down copies of the original image—and ultimately returns to the original image.
The discrete cat map describes the phase space
Phase space
In mathematics and physics, a phase space, introduced by Willard Gibbs in 1901, is a space in which all possible states of a system are represented, with each possible state of the system corresponding to one unique point in the phase space...
flow corresponding to the discrete dynamics of a bead hopping from site qt (0 ≤ qt < N) to site qt+1 on a circular ring with circumference N, according to the second order equation:
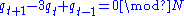
Defining the momentum variable pt = qt - qt-1, the above second order dynamics can be re-written as a mapping of the square 0 ≤ q, p < N (the phase space
Phase space
In mathematics and physics, a phase space, introduced by Willard Gibbs in 1901, is a space in which all possible states of a system are represented, with each possible state of the system corresponding to one unique point in the phase space...
of the discrete dynamical system) onto itself:
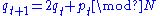
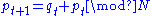
This Arnold cat mapping shows mixing
Mixing (physics)
In physics, a dynamical system is said to be mixing if the phase space of the system becomes strongly intertwined, according to at least one of several mathematical definitions. For example, a measure-preserving transformation T is said to be strong mixing ifwhenever A and B are any measurable...
behavior typical for chaotic systems. However, since the transformation has a determinant
Determinant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
equal to unity, it is area-preserving and therefore invertible the inverse transformation being:
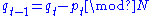
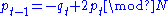
For real variables q and p, it is common to set N = 1. In that case a mapping of the unit square with periodic boundary conditions onto itself results.
When N is set to an integer value, the position and momentum variables can be restricted to integers and the mapping becomes a mapping of a toroidial square grid of points onto itself. Such an integer cat map is commonly used to demonstrate mixing
Mixing (physics)
In physics, a dynamical system is said to be mixing if the phase space of the system becomes strongly intertwined, according to at least one of several mathematical definitions. For example, a measure-preserving transformation T is said to be strong mixing ifwhenever A and B are any measurable...
behavior with Poincaré recurrence
Poincaré recurrence theorem
In mathematics, the Poincaré recurrence theorem states that certain systems will, after a sufficiently long time, return to a state very close to the initial state. The Poincaré recurrence time is the length of time elapsed until the recurrence. The result applies to physical systems in which...
utilising digital images. The number of iterations needed to restore the image can be shown never to exceed 3N.
For an image, the relationship between iterations could be expressed as follows:
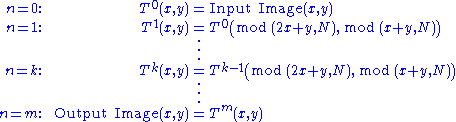
External links
- A description and demonstration, using an image of the EarthEarthEarth is the third planet from the Sun, and the densest and fifth-largest of the eight planets in the Solar System. It is also the largest of the Solar System's four terrestrial planets...
as an example - Effect of randomisation of initial conditions on recurrence time
- Arnold's Cat Map by Enrique Zeleny, The Wolfram Demonstrations Project.
- Arnold's Cat Map, David Arnold.

