Armstrong's axioms
Encyclopedia
Armstrong's axioms are a set of axiom
s (or, more precisely, inference rules) used to infer all the functional dependencies
on a relational database
. They were developed by William W. Armstrong
on his paper. The axioms are sound
in that they generate only functional dependencies in the closure
of a set of functional dependencies (denoted as F+) when applied to that set (denoted as F). They are also complete
in that repeated application of these rules will generate all functional dependencies in the closure F+.
More formally, let <
( 
), 
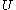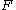> denote a relational scheme over the set of attributes 
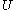with a set of functional dependencies 
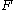. We say that a functional dependency 
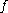is logically implied by 
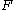,and denote it with 
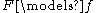if and only if for every instance 
of 
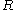that satisfies the functional dependencies in 
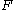, r also satisfies 
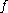. We denote by 
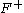the set of all functional dependencies that are logically implied by F.
Furthermore, with respect to a set of inference rules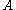
, we say that a functional dependency 
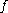is derivable from the functional dependencies in 
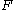by the set of inference rules 
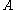, and we denote it by 
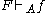if and only if 
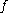is obtainable by means of repeatedly applying the inference rules in 
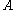to functional dependencies in 
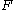. We denote by 
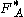the set of all functional dependencies that are derivable from 
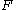by inference rules in 
.
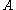Then, a set of inference rules
is sound if and only if the following holds:
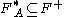
that is to say, we cannot derive by means of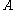
functional dependencies that are not logically implied by 
.
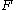The set of inference rules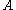
is said to be complete if the following holds:
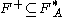
more simply put, we are able to derive by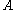
all the functional dependencies that are logically implied by 
.
(
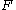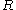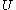) be a relation scheme over the set of attributes 
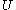. Henceforth we will denote by letters 
, 
, 
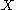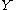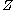any subset of 
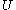and, for short, the union of two sets of attributes 
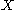and 
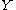by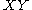 
instead of the usual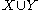 
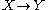, then 
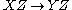for any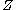 
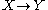and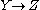 
, then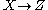 
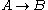and 
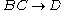then 
Axiom
In traditional logic, an axiom or postulate is a proposition that is not proven or demonstrated but considered either to be self-evident or to define and delimit the realm of analysis. In other words, an axiom is a logical statement that is assumed to be true...
s (or, more precisely, inference rules) used to infer all the functional dependencies
Functional dependency
A functional dependency is a constraint between two sets of attributes in a relation from a database.Given a relation R, a set of attributes X in R is said to functionally determine another attribute Y, also in R, if, and only if, each X value is associated with precisely one Y value...
on a relational database
Relational database
A relational database is a database that conforms to relational model theory. The software used in a relational database is called a relational database management system . Colloquial use of the term "relational database" may refer to the RDBMS software, or the relational database itself...
. They were developed by William W. Armstrong
William Ward Armstrong
William Ward Armstrong is a Canadian mathematician and computer scientist. He earned his Ph.D. from the University of British Columbia in 1966 and is most known as the originator Armstrong's axioms of dependency in a Relational database.-Works:...
on his paper. The axioms are sound
Soundness
In mathematical logic, a logical system has the soundness property if and only if its inference rules prove only formulas that are valid with respect to its semantics. In most cases, this comes down to its rules having the property of preserving truth, but this is not the case in general. The word...
in that they generate only functional dependencies in the closure
Closure (mathematics)
In mathematics, a set is said to be closed under some operation if performance of that operation on members of the set always produces a unique member of the same set. For example, the real numbers are closed under subtraction, but the natural numbers are not: 3 and 8 are both natural numbers, but...
of a set of functional dependencies (denoted as F+) when applied to that set (denoted as F). They are also complete
Completeness
In general, an object is complete if nothing needs to be added to it. This notion is made more specific in various fields.-Logical completeness:In logic, semantic completeness is the converse of soundness for formal systems...
in that repeated application of these rules will generate all functional dependencies in the closure F+.
More formally, let <
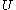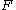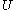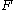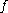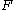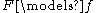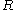( ), > denote a relational scheme over the set of attributes with a set of functional dependencies . We say that a functional dependency is logically implied by ,and denote it with if and only if for every instance of that satisfies the functional dependencies in 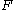, r also satisfies 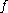. We denote by 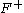the set of all functional dependencies that are logically implied by F.Furthermore, with respect to a set of inference rules
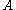, we say that a functional dependency 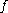is derivable from the functional dependencies in 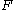by the set of inference rules 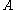, and we denote it by 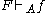if and only if 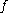is obtainable by means of repeatedly applying the inference rules in 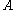to functional dependencies in 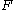. We denote by 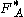the set of all functional dependencies that are derivable from 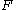by inference rules in 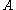.Then, a set of inference rules
is sound if and only if the following holds: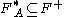that is to say, we cannot derive by means of
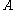functional dependencies that are not logically implied by 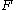.The set of inference rules
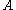is said to be complete if the following holds: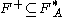more simply put, we are able to derive by
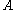all the functional dependencies that are logically implied by 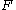.Axioms
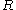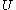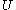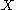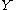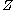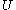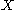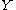Let() be a relation scheme over the set of attributes . Henceforth we will denote by letters , , any subset of and, for short, the union of two sets of attributes and by 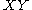instead of the usual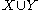 Axiom of augmentation
If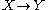, then 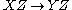for any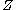 Axiom of transitivity
If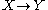 and 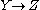, then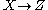 Pseudo Transitivity
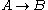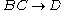If and then