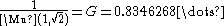Arithmetic-geometric mean
Encyclopedia
In mathematics
, the arithmetic-geometric mean (AGM) of two positive real number
s and is defined as follows:
First compute the arithmetic mean
of and and call it . Next compute the geometric mean
of and and call it ; this is the square root
of the product :

 .
.
Then iterate this operation with taking the place of and taking the place of . In this way, two sequence
s and are defined:
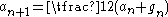
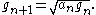
These two sequences converge
to the same number, which is the arithmetic-geometric mean of and ; it is denoted by , or sometimes by .
This can be used for algorithmic purposes as in the AGM method
.
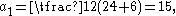

and then iterate as follows:
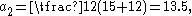
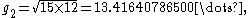
etc.
The first four iterations give the following values:
The arithmetic-geometric mean of 24 and 6 is the common limit of these two sequences, which is approximately 13.45817148173.
); as a consequence, is an increasing sequence, is a decreasing sequence, and . These are strict inequalities if .
is thus a number between the geometric and arithmetic mean of and ; in particular it is between and .
If , then .
There is an integral-form expression for :
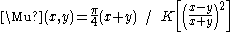
where is the complete elliptic integral of the first kind
:

Indeed, since the arithmetic-geometric process converges so quickly, it provides an effective way to compute elliptic integrals via this formula.
The reciprocal of the arithmetic-geometric mean of 1 and the square root of 2
is called Gauss's constant
.
named after Carl Friedrich Gauss
.
The geometric-harmonic mean
can be calculated by an analogous method, using sequences of geometric and harmonic
means. The arithmetic-harmonic mean can be similarly defined, but takes the same value as the geometric mean
.
we can conclude that:
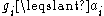
and thus

that is, the sequence is nondecreasing.
Furthermore, it is easy to see that it is also bounded above by the larger of and (which follows from the fact that both arithmetic and geometric means of two numbers both lie between them). Thus by the monotone convergence theorem the sequence is convergent, so there exists a such that:
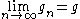
However, we can also see that:
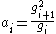
and so:
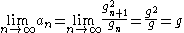
Q.E.D.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the arithmetic-geometric mean (AGM) of two positive real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s and is defined as follows:
First compute the arithmetic mean
Arithmetic mean
In mathematics and statistics, the arithmetic mean, often referred to as simply the mean or average when the context is clear, is a method to derive the central tendency of a sample space...
of and and call it . Next compute the geometric mean
Geometric mean
The geometric mean, in mathematics, is a type of mean or average, which indicates the central tendency or typical value of a set of numbers. It is similar to the arithmetic mean, except that the numbers are multiplied and then the nth root of the resulting product is taken.For instance, the...
of and and call it ; this is the square root
Square root
In mathematics, a square root of a number x is a number r such that r2 = x, or, in other words, a number r whose square is x...
of the product :

 .
.Then iterate this operation with taking the place of and taking the place of . In this way, two sequence
Sequence
In mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
s and are defined:
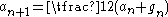
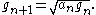
These two sequences converge
Limit of a sequence
The limit of a sequence is, intuitively, the unique number or point L such that the terms of the sequence become arbitrarily close to L for "large" values of n...
to the same number, which is the arithmetic-geometric mean of and ; it is denoted by , or sometimes by .
This can be used for algorithmic purposes as in the AGM method
AGM method
In mathematics, the AGM method makes it possible to construct fast algorithms for calculation of exponential and trigonometric functions, and some mathematical constants and in particular, to quickly compute \pi....
.
Example
To find the arithmetic-geometric mean of and , first calculate their arithmetic mean and geometric mean, thus: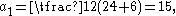

and then iterate as follows:
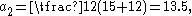
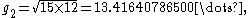
etc.
The first four iterations give the following values:
| 0 | 24 | 6 |
| 1 | 15 | 12 |
| 2 | 13.5 | 13.41640786500... |
| 3 | 13.45820393250... | 13.45813903099... |
| 4 | 13.45817148175... | 13.45817148171... |
The arithmetic-geometric mean of 24 and 6 is the common limit of these two sequences, which is approximately 13.45817148173.
Properties
The geometric mean of two positive numbers is never bigger than the arithmetic mean (see inequality of arithmetic and geometric meansInequality of arithmetic and geometric means
In mathematics, the inequality of arithmetic and geometric means, or more briefly the AM–GM inequality, states that the arithmetic mean of a list of non-negative real numbers is greater than or equal to the geometric mean of the same list; and further, that the two means are equal if and only if...
); as a consequence, is an increasing sequence, is a decreasing sequence, and . These are strict inequalities if .
is thus a number between the geometric and arithmetic mean of and ; in particular it is between and .
If , then .
There is an integral-form expression for :
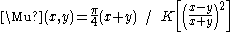
where is the complete elliptic integral of the first kind
Elliptic integral
In integral calculus, elliptic integrals originally arose in connection with the problem of giving the arc length of an ellipse. They were first studied by Giulio Fagnano and Leonhard Euler...
:

Indeed, since the arithmetic-geometric process converges so quickly, it provides an effective way to compute elliptic integrals via this formula.
The reciprocal of the arithmetic-geometric mean of 1 and the square root of 2
Square root of 2
The square root of 2, often known as root 2, is the positive algebraic number that, when multiplied by itself, gives the number 2. It is more precisely called the principal square root of 2, to distinguish it from the negative number with the same property.Geometrically the square root of 2 is the...
is called Gauss's constant
Gauss's constant
In mathematics, Gauss's constant, denoted by G, is defined as the reciprocal of the arithmetic-geometric mean of 1 and the square root of 2:The constant is named after Carl Friedrich Gauss, who on May 30, 1799 discovered thatso that...
.
named after Carl Friedrich Gauss
Carl Friedrich Gauss
Johann Carl Friedrich Gauss was a German mathematician and scientist who contributed significantly to many fields, including number theory, statistics, analysis, differential geometry, geodesy, geophysics, electrostatics, astronomy and optics.Sometimes referred to as the Princeps mathematicorum...
.
The geometric-harmonic mean
Geometric-harmonic mean
In mathematics, the geometric-harmonic mean M of two positive real numbers x and y is defined as follows: we form the geometric mean of g0 = x and h0 = y and call it g1, i.e. g1 is the square root of xy. We also form the harmonic mean of x and y and call it h1, i.e...
can be calculated by an analogous method, using sequences of geometric and harmonic
Harmonic mean
In mathematics, the harmonic mean is one of several kinds of average. Typically, it is appropriate for situations when the average of rates is desired....
means. The arithmetic-harmonic mean can be similarly defined, but takes the same value as the geometric mean
Geometric mean
The geometric mean, in mathematics, is a type of mean or average, which indicates the central tendency or typical value of a set of numbers. It is similar to the arithmetic mean, except that the numbers are multiplied and then the nth root of the resulting product is taken.For instance, the...
.
Proof of existence
From inequality of arithmetic and geometric meansInequality of arithmetic and geometric means
In mathematics, the inequality of arithmetic and geometric means, or more briefly the AM–GM inequality, states that the arithmetic mean of a list of non-negative real numbers is greater than or equal to the geometric mean of the same list; and further, that the two means are equal if and only if...
we can conclude that:
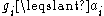
and thus

that is, the sequence is nondecreasing.
Furthermore, it is easy to see that it is also bounded above by the larger of and (which follows from the fact that both arithmetic and geometric means of two numbers both lie between them). Thus by the monotone convergence theorem the sequence is convergent, so there exists a such that:
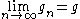
However, we can also see that:
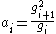
and so:
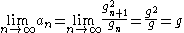
Q.E.D.
Q.E.D.
Q.E.D. is an initialism of the Latin phrase , which translates as "which was to be demonstrated". The phrase is traditionally placed in its abbreviated form at the end of a mathematical proof or philosophical argument when what was specified in the enunciation — and in the setting-out —...
See also
- Generalized meanGeneralized meanIn mathematics, a generalized mean, also known as power mean or Hölder mean , is an abstraction of the Pythagorean means including arithmetic, geometric, and harmonic means.-Definition:...
- Inequality of arithmetic and geometric meansInequality of arithmetic and geometric meansIn mathematics, the inequality of arithmetic and geometric means, or more briefly the AM–GM inequality, states that the arithmetic mean of a list of non-negative real numbers is greater than or equal to the geometric mean of the same list; and further, that the two means are equal if and only if...
- Gauss–Legendre algorithm