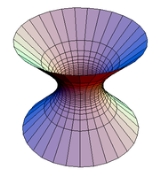
Anti de Sitter space
Overview
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
and physics
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
, n-dimensional anti de Sitter space, sometimes written
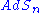 , is a maximally symmetric Lorentzian manifold with constant negative scalar curvature
, is a maximally symmetric Lorentzian manifold with constant negative scalar curvatureScalar curvature
In Riemannian geometry, the scalar curvature is the simplest curvature invariant of a Riemannian manifold. To each point on a Riemannian manifold, it assigns a single real number determined by the intrinsic geometry of the manifold near that point...
. It is the Lorentzian analogue of n-dimensional hyperbolic space
Hyperbolic space
In mathematics, hyperbolic space is a type of non-Euclidean geometry. Whereas spherical geometry has a constant positive curvature, hyperbolic geometry has a negative curvature: every point in hyperbolic space is a saddle point...
, just as Minkowski space
Minkowski space
In physics and mathematics, Minkowski space or Minkowski spacetime is the mathematical setting in which Einstein's theory of special relativity is most conveniently formulated...
and de Sitter space
De Sitter space
In mathematics and physics, a de Sitter space is the analog in Minkowski space, or spacetime, of a sphere in ordinary, Euclidean space. The n-dimensional de Sitter space , denoted dS_n, is the Lorentzian manifold analog of an n-sphere ; it is maximally symmetric, has constant positive curvature,...
are the analogues of Euclidean
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
and elliptical spaces respectively.
It is best known for its role in the AdS/CFT correspondence
AdS/CFT correspondence
In physics, the AdS/CFT correspondence , sometimes called the Maldacena duality, is the conjectured equivalence between a string theory and gravity defined on one space, and a quantum field theory without gravity defined on the conformal boundary of this space, whose dimension is lower by one or more...
.
In the language of general relativity
General relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
, anti de Sitter space is a maximally symmetric, vacuum solution
Vacuum solution
A vacuum solution is a solution of a field equation in which the sources of the field are taken to be identically zero. That is, such field equations are written without matter interaction .-Examples:...
of Einstein's field equation with a negative (attractive) cosmological constant
Cosmological constant
In physical cosmology, the cosmological constant was proposed by Albert Einstein as a modification of his original theory of general relativity to achieve a stationary universe...
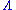 (corresponding to a negative vacuum energy density and positive pressure).
(corresponding to a negative vacuum energy density and positive pressure).In mathematics, anti de Sitter space is sometimes defined more generally as a space of arbitrary signature
Metric signature
The signature of a metric tensor is the number of positive and negative eigenvalues of the metric. That is, the corresponding real symmetric matrix is diagonalised, and the diagonal entries of each sign counted...
(p,q).
Unanswered Questions

