
Anscombe's quartet
Encyclopedia
Anscombe's quartet comprises four datasets that have identical simple statistical properties, yet appear very different when graphed. Each dataset consists of eleven (x,y) points. They were constructed in 1973 by the statistician
F.J. Anscombe to demonstrate both the importance of graphing data before analysing it and the effect of outlier
s on statistical properties.
For all four datasets:
The first one (top left) seems to be distributed normally, and corresponds to what one would expect when considering two variables correlated and following the assumption of normality. The second one (top right) is not distributed normally; while an obvious relationship between the two variables can be observed, it is not linear, and the Pearson correlation coefficient is not relevant. In the third case (bottom left), the distribution is linear, but with a different regression line, which is offset by the one outlier
which exerts enough influence to alter the regression line and lower the correlation coefficient from 1 to 0.81. Finally, the fourth example (bottom right) shows another example when one outlier is enough to produce a high correlation coefficient, even though the relationship between the two variables is not linear.
Edward Tufte
uses the quartet to emphasize the importance of looking at one's data before analyzing it in the first page of the first chapter of his book, The Visual Display of Quantitative Information.
The datasets are as follows. The x values are the same for the first three datasets.
A procedure to generate similar data sets with identical statistics and dissimilar graphics can be found in the references.
Statistician
A statistician is someone who works with theoretical or applied statistics. The profession exists in both the private and public sectors. The core of that work is to measure, interpret, and describe the world and human activity patterns within it...
F.J. Anscombe to demonstrate both the importance of graphing data before analysing it and the effect of outlier
Outlier
In statistics, an outlier is an observation that is numerically distant from the rest of the data. Grubbs defined an outlier as: An outlying observation, or outlier, is one that appears to deviate markedly from other members of the sample in which it occurs....
s on statistical properties.
For all four datasets:
| Property | Value |
|---|---|
| Mean Mean In statistics, mean has two related meanings:* the arithmetic mean .* the expected value of a random variable, which is also called the population mean.... of x in each case |
9 exact |
| Variance Variance In probability theory and statistics, the variance is a measure of how far a set of numbers is spread out. It is one of several descriptors of a probability distribution, describing how far the numbers lie from the mean . In particular, the variance is one of the moments of a distribution... of x in each case |
11 exact |
| Mean of y in each case | 7.50 (to 2 d.p.) |
| Variance of y in each case | 4.122 or 4.127 (to 3 d.p.) |
| Correlation Correlation In statistics, dependence refers to any statistical relationship between two random variables or two sets of data. Correlation refers to any of a broad class of statistical relationships involving dependence.... between x and y in each case |
0.816 (to 3 d.p.) |
| Linear regression Linear regression In statistics, linear regression is an approach to modeling the relationship between a scalar variable y and one or more explanatory variables denoted X. The case of one explanatory variable is called simple regression... line in each case |
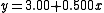 (to 2 d.p. and 3 d.p. resp.) (to 2 d.p. and 3 d.p. resp.) |
The first one (top left) seems to be distributed normally, and corresponds to what one would expect when considering two variables correlated and following the assumption of normality. The second one (top right) is not distributed normally; while an obvious relationship between the two variables can be observed, it is not linear, and the Pearson correlation coefficient is not relevant. In the third case (bottom left), the distribution is linear, but with a different regression line, which is offset by the one outlier
Outlier
In statistics, an outlier is an observation that is numerically distant from the rest of the data. Grubbs defined an outlier as: An outlying observation, or outlier, is one that appears to deviate markedly from other members of the sample in which it occurs....
which exerts enough influence to alter the regression line and lower the correlation coefficient from 1 to 0.81. Finally, the fourth example (bottom right) shows another example when one outlier is enough to produce a high correlation coefficient, even though the relationship between the two variables is not linear.
Edward Tufte
Edward Tufte
Edward Rolf Tufte is an American statistician and professor emeritus of political science, statistics, and computer science at Yale University. He is noted for his writings on information design and as a pioneer in the field of data visualization....
uses the quartet to emphasize the importance of looking at one's data before analyzing it in the first page of the first chapter of his book, The Visual Display of Quantitative Information.
The datasets are as follows. The x values are the same for the first three datasets.
| I | II | III | IV | ||||
|---|---|---|---|---|---|---|---|
| x | y | x | y | x | y | x | y |
| 10.0 | 8.04 | 10.0 | 9.14 | 10.0 | 7.46 | 8.0 | 6.58 |
| 8.0 | 6.95 | 8.0 | 8.14 | 8.0 | 6.77 | 8.0 | 5.76 |
| 13.0 | 7.58 | 13.0 | 8.74 | 13.0 | 12.74 | 8.0 | 7.71 |
| 9.0 | 8.81 | 9.0 | 8.77 | 9.0 | 7.11 | 8.0 | 8.84 |
| 11.0 | 8.33 | 11.0 | 9.26 | 11.0 | 7.81 | 8.0 | 8.47 |
| 14.0 | 9.96 | 14.0 | 8.10 | 14.0 | 8.84 | 8.0 | 7.04 |
| 6.0 | 7.24 | 6.0 | 6.13 | 6.0 | 6.08 | 8.0 | 5.25 |
| 4.0 | 4.26 | 4.0 | 3.10 | 4.0 | 5.39 | 19.0 | 12.50 |
| 12.0 | 10.84 | 12.0 | 9.13 | 12.0 | 8.15 | 8.0 | 5.56 |
| 7.0 | 4.82 | 7.0 | 7.26 | 7.0 | 6.42 | 8.0 | 7.91 |
| 5.0 | 5.68 | 5.0 | 4.74 | 5.0 | 5.73 | 8.0 | 6.89 |
A procedure to generate similar data sets with identical statistics and dissimilar graphics can be found in the references.

