Activity coefficient
Encyclopedia
An activity coefficient is a factor used in thermodynamics
to account for deviations from ideal behaviour in a mixture
of chemical substance
s. In an ideal mixture, the interactions between each pair of chemical species
are the same (or more formally, the enthalpy
of mixing is zero) and, as a result, properties of the mixtures can be expressed directly in terms
of simple concentration
s or partial pressure
s of the substances present e.g. Raoult's law. Deviations from ideality are accommodated by modifying the concentration by an activity coefficient. Analogously, expressions involving gases can be adjusted for non-ideality by scaling partial pressure
s by a fugacity
coefficient.
The concept of activity coefficient is closely linked to that of activity in chemistry
.
,
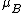, of a substance B in an ideal mixture is given by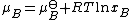
where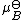
is the chemical potential in the standard state
and xB is the mole fraction of the substance in the mixture.
This is generalised to include non-ideal behavior by writing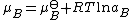
when
is the activity of the substance in the mixture with
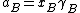
where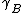
is the activity coefficient. As 
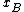approaches 1, the substance behaves as if it were ideal, and thus 
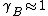, which is known as Raoult's Law.
For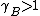
and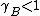 
substance B shows positive and negative deviation from Raoult's law respectively. A positive deviation implies that the substance becomes more volatile.
For the case where
goes to zero, the activity coefficient of substance B approaches a constant; this relationship is Henry's Law for the solvent. These relationships are related to each other through the Gibbs-Duhem equation.
Note that in general activity coefficients are dimensionless.
Modifying mole fractions or concentrations by activity coefficients gives the effective activities of the components, and hence allows expressions such as Raoult's law and equilibrium constants constants to be applied to both ideal and non-ideal mixtures.
Knowledge of activity coefficients is particularly important in the context of electrochemistry
since the behaviour of electrolyte
solutions is often far from ideal, due the effects of the ionic atmosphere
. Additionally, they are particularly important in the context of soil chemistry
due to the low volumes of solvent and, consequently, the high concentration of electrolytes.
change for the reactions,
, is equal to the difference between these sums and therefore, at equilibrium, is equal to zero. Thus, for an equilibrium such as
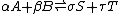
Substitute in the expressions for the chemical potential of each reactant:
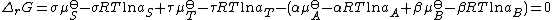
Upon rearrangement this expression becomes
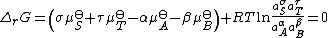
The sum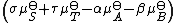
is the standard free energy change for the reaction, 
. Therefore
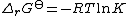
K is the equilibrium constant. Note that activities and equilibrium constants are dimensionless numbers.
This derivation serves two purposes. It shows the relationship between standard free energy change and equilibrium constant. It also shows that an equilibrium constant is defined as a quotient of activities. In practical terms this is inconvenient. When each activity is replaced by the product of a concentration and an activity coefficient, the equilibrium constant is defined as
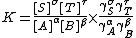
where [S] denotes the concentration
of S, etc. In practice equilibrium constants are determined
in a medium such that the quotient of activity coefficient is constant and can be ignored, leading to the usual expression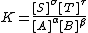
which applies under the conditions that the activity quotient has a particular (constant) value.
or extensions such as Davies equation
, Pitzer equations
or TCPC model.specific ion interaction theory
(SIT) may also be used. Alternatively correlative methods such as UNIQUAC
, NRTL, MOSCED
or UNIFAC
may be employed, provided fitted component-specific or model parameters are available.
A new alternative for activity coefficients prediction, which is less dependent on model parameters, is the COSMO-RS method. In this methods the required information comes from quantum mechanics calculations specific to each molecule (sigma profiles) combined with a statistical thermodynamics treatment of surface segments.
For uncharged species, the activity coefficient γ0 mostly follows a "salting-out" model:
This simple model predicts activities of many species (dissolved undissociated gases such as CO2, H2S, NH3, undissociated acids and bases) to high ionic strengths (up to 5 mol/kg). The value of the constant b for CO2 is 0.11 at 10 °C and 0.20 at 330 °C.
For water (solvent), the activity aw can be calculated using:
φ
where ν is the number of ions produced from the dissociation of one molecule of the dissolved salt, m is the molal concentration of the salt dissolved in water, φ is the osmotic coefficient
of water, and the constant 55.51 represents the molal concentration of water. In the above equation, the activity of a solvent (here water) is represented as inversely proportional to the number of particles of salt versus that of the solvent.
Thermodynamics
Thermodynamics is a physical science that studies the effects on material bodies, and on radiation in regions of space, of transfer of heat and of work done on or by the bodies or radiation...
to account for deviations from ideal behaviour in a mixture
Mixture
In chemistry, a mixture is a material system made up by two or more different substances which are mixed together but are not combined chemically...
of chemical substance
Chemical substance
In chemistry, a chemical substance is a form of matter that has constant chemical composition and characteristic properties. It cannot be separated into components by physical separation methods, i.e. without breaking chemical bonds. They can be solids, liquids or gases.Chemical substances are...
s. In an ideal mixture, the interactions between each pair of chemical species
Chemical species
Chemical species are atoms, molecules, molecular fragments, ions, etc., being subjected to a chemical process or to a measurement. Generally, a chemical species can be defined as an ensemble of chemically identical molecular entities that can explore the same set of molecular energy levels on a...
are the same (or more formally, the enthalpy
Enthalpy
Enthalpy is a measure of the total energy of a thermodynamic system. It includes the internal energy, which is the energy required to create a system, and the amount of energy required to make room for it by displacing its environment and establishing its volume and pressure.Enthalpy is a...
of mixing is zero) and, as a result, properties of the mixtures can be expressed directly in terms
of simple concentration
Concentration
In chemistry, concentration is defined as the abundance of a constituent divided by the total volume of a mixture. Four types can be distinguished: mass concentration, molar concentration, number concentration, and volume concentration...
s or partial pressure
Partial pressure
In a mixture of ideal gases, each gas has a partial pressure which is the pressure which the gas would have if it alone occupied the volume. The total pressure of a gas mixture is the sum of the partial pressures of each individual gas in the mixture....
s of the substances present e.g. Raoult's law. Deviations from ideality are accommodated by modifying the concentration by an activity coefficient. Analogously, expressions involving gases can be adjusted for non-ideality by scaling partial pressure
Partial pressure
In a mixture of ideal gases, each gas has a partial pressure which is the pressure which the gas would have if it alone occupied the volume. The total pressure of a gas mixture is the sum of the partial pressures of each individual gas in the mixture....
s by a fugacity
Fugacity
In chemical thermodynamics, the fugacity of a real gas is an effective pressure which replaces the true mechanical pressure in accurate chemical equilibrium calculations. It is equal to the pressure of an ideal gas which has the same chemical potential as the real gas. For example, nitrogen gas ...
coefficient.
The concept of activity coefficient is closely linked to that of activity in chemistry
Activity (chemistry)
In chemical thermodynamics, activity is a measure of the “effective concentration” of a species in a mixture, meaning that the species' chemical potential depends on the activity of a real solution in the same way that it would depend on concentration for an ideal solution.By convention, activity...
.
Thermodynamics
The chemical potentialChemical potential
Chemical potential, symbolized by μ, is a measure first described by the American engineer, chemist and mathematical physicist Josiah Willard Gibbs. It is the potential that a substance has to produce in order to alter a system...
,
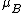, of a substance B in an ideal mixture is given by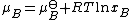where
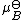is the chemical potential in the standard stateStandard state
In chemistry, the standard state of a material is a reference point used to calculate its properties under different conditions. In principle, the choice of standard state is arbitrary, although the International Union of Pure and Applied Chemistry recommends a conventional set of standard states...
and xB is the mole fraction of the substance in the mixture.
This is generalised to include non-ideal behavior by writing
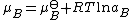
when
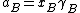
is the activity of the substance in the mixture withwhere
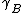is the activity coefficient. As 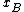approaches 1, the substance behaves as if it were ideal, and thus 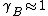, which is known as Raoult's Law.For
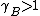and 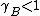substance B shows positive and negative deviation from Raoult's law respectively. A positive deviation implies that the substance becomes more volatile.For the case where
goes to zero, the activity coefficient of substance B approaches a constant; this relationship is Henry's Law for the solvent. These relationships are related to each other through the Gibbs-Duhem equation.Note that in general activity coefficients are dimensionless.
Modifying mole fractions or concentrations by activity coefficients gives the effective activities of the components, and hence allows expressions such as Raoult's law and equilibrium constants constants to be applied to both ideal and non-ideal mixtures.
Knowledge of activity coefficients is particularly important in the context of electrochemistry
Electrochemistry
Electrochemistry is a branch of chemistry that studies chemical reactions which take place in a solution at the interface of an electron conductor and an ionic conductor , and which involve electron transfer between the electrode and the electrolyte or species in solution.If a chemical reaction is...
since the behaviour of electrolyte
Electrolyte
In chemistry, an electrolyte is any substance containing free ions that make the substance electrically conductive. The most typical electrolyte is an ionic solution, but molten electrolytes and solid electrolytes are also possible....
solutions is often far from ideal, due the effects of the ionic atmosphere
Ionic atmosphere
Ionic Atmosphere is a concept employed in Debye-Hückel theory which explains the conductivity behaviour of electrolytic solutions. It can be generally defined as the area at which a charged entity is capable of attracting an entity of the opposite charge....
. Additionally, they are particularly important in the context of soil chemistry
Soil chemistry
Soil chemistry is the study of the chemical characteristics of soil. Soil chemistry is affected by mineral composition, organic matter and environmental factors.-History:...
due to the low volumes of solvent and, consequently, the high concentration of electrolytes.
Application to chemical equilibrium
At equilibrium, the sum of the chemical potentials of the reactants is equal to the sum of the chemical potentials of the products. The Gibbs free energyGibbs free energy
In thermodynamics, the Gibbs free energy is a thermodynamic potential that measures the "useful" or process-initiating work obtainable from a thermodynamic system at a constant temperature and pressure...
change for the reactions,
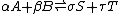
, is equal to the difference between these sums and therefore, at equilibrium, is equal to zero. Thus, for an equilibrium such asSubstitute in the expressions for the chemical potential of each reactant:
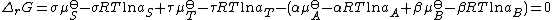
Upon rearrangement this expression becomes
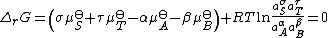
The sum
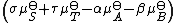is the standard free energy change for the reaction, . Therefore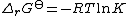K is the equilibrium constant. Note that activities and equilibrium constants are dimensionless numbers.
This derivation serves two purposes. It shows the relationship between standard free energy change and equilibrium constant. It also shows that an equilibrium constant is defined as a quotient of activities. In practical terms this is inconvenient. When each activity is replaced by the product of a concentration and an activity coefficient, the equilibrium constant is defined as
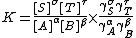
where [S] denotes the concentration
Concentration
In chemistry, concentration is defined as the abundance of a constituent divided by the total volume of a mixture. Four types can be distinguished: mass concentration, molar concentration, number concentration, and volume concentration...
of S, etc. In practice equilibrium constants are determined
Determination of equilibrium constants
Equilibrium constants are determined in order to quantify chemical equilibria. When an equilibrium constant is expressed as a concentration quotient,K=\frac...
in a medium such that the quotient of activity coefficient is constant and can be ignored, leading to the usual expression
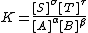
which applies under the conditions that the activity quotient has a particular (constant) value.
Measurement and prediction of activity coefficients
Activity coefficients may be measured experimentally or calculated theoretically, using the Debye-Hückel equationDebye-Hückel equation
The Debye–Hückel equation and Debye–Hückel limiting law, were derived by Peter Debye and Erich Hückel, who developed a theory with which to calculate activity coefficients of electrolyte solutions. Activities, rather than concentrations, are needed in many chemical calculations because solutions...
or extensions such as Davies equation
Davies equation
The Davies equation is an empirical extension of Debye–Hückel theory which can be used to calculate activity coefficients of electrolyte solutions at relatively high concentrations. The equation, originally published in 1938, was refined by fitting to experimental data...
, Pitzer equations
Pitzer equations
Pitzer equations are important for the understanding of the behaviour of ions dissolved in natural waters such as rivers, lakes and sea-water. The parameters of the Pitzer equations are linear combinations of parameters, of a virial expansion of the excess Gibbs free energy, which characterise...
or TCPC model.specific ion interaction theory
Specific ion interaction theory
Specific ion Interaction Theory is a theory used to estimate single-ion activity coefficients in electrolyte solutions at relatively high concentrations. It does so by taking into consideration interaction coefficients between the various ions present in solution...
(SIT) may also be used. Alternatively correlative methods such as UNIQUAC
UNIQUAC
UNIQUAC is an activity coefficient model used in description of phase equilibria.The model is a so-called lattice model and has been derived from a first order approximation...
, NRTL, MOSCED
MOSCED
MOSCED is a thermodynamic model for the estimation of limiting activity coefficients . From a historical point of view MOSCED can be regarded as an improved modification of the Hansen method and the Hildebrand solubility model...
or UNIFAC
UNIFAC
The UNIversal Functional Activity Coefficient method is a semi-empirical system for the prediction of non-electrolyte activity estimation in non-ideal mixtures. UNIFAC uses the functional groups present on the molecules that make up the liquid mixture to calculate activity coefficients...
may be employed, provided fitted component-specific or model parameters are available.
A new alternative for activity coefficients prediction, which is less dependent on model parameters, is the COSMO-RS method. In this methods the required information comes from quantum mechanics calculations specific to each molecule (sigma profiles) combined with a statistical thermodynamics treatment of surface segments.
For uncharged species, the activity coefficient γ0 mostly follows a "salting-out" model:
This simple model predicts activities of many species (dissolved undissociated gases such as CO2, H2S, NH3, undissociated acids and bases) to high ionic strengths (up to 5 mol/kg). The value of the constant b for CO2 is 0.11 at 10 °C and 0.20 at 330 °C.
For water (solvent), the activity aw can be calculated using:
φwhere ν is the number of ions produced from the dissociation of one molecule of the dissolved salt, m is the molal concentration of the salt dissolved in water, φ is the osmotic coefficient
Osmotic coefficient
An osmotic coefficient φ is a quantity which characterises the deviation of a solvent from ideal behaviour, referenced to Raoult's law. The osmotic coefficient on a molality basis is defined by:and on an amount fraction basis by:...
of water, and the constant 55.51 represents the molal concentration of water. In the above equation, the activity of a solvent (here water) is represented as inversely proportional to the number of particles of salt versus that of the solvent.