In statistics

Statistics

Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....

, the absolute deviation of an element of a data set

Data set

A data set is a collection of data, usually presented in tabular form. Each column represents a particular variable. Each row corresponds to a given member of the data set in question. Its values for each of the variables, such as height and weight of an object or values of random numbers. Each...

 is the absolute difference

Absolute difference

The absolute difference of two real numbers x, y is given by |x − y|, the absolute value of their difference. It describes the distance on the real line between the points corresponding to x and y...

 between that element and a given point. Typically the point from which the deviation is measured is a measure of central tendency

Central tendency

In statistics, the term central tendency relates to the way in which quantitative data is clustered around some value. A measure of central tendency is a way of specifying - central value...

, most often the median

Median

In probability theory and statistics, a median is described as the numerical value separating the higher half of a sample, a population, or a probability distribution, from the lower half. The median of a finite list of numbers can be found by arranging all the observations from lowest value to...

 or sometimes the mean

Mean

In statistics, mean has two related meanings:* the arithmetic mean .* the expected value of a random variable, which is also called the population mean....

 of the data set.


where

D_i is the absolute deviation,

x_i is the data element

and m(X) is the chosen measure of central tendency

Central tendency

In statistics, the term central tendency relates to the way in which quantitative data is clustered around some value. A measure of central tendency is a way of specifying - central value...

 of the data set—sometimes the mean

Mean

In statistics, mean has two related meanings:* the arithmetic mean .* the expected value of a random variable, which is also called the population mean....

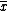 (), but most often the median

Median

In probability theory and statistics, a median is described as the numerical value separating the higher half of a sample, a population, or a probability distribution, from the lower half. The median of a finite list of numbers can be found by arranging all the observations from lowest value to...

.

Several measures of statistical dispersion

Statistical dispersion

In statistics, statistical dispersion is variability or spread in a variable or a probability distribution...

 are defined in terms of the absolute deviation.
The average absolute deviation, or simply average deviation of a data set is the average

Average

In mathematics, an average, or central tendency of a data set is a measure of the "middle" value of the data set. Average is one form of central tendency. Not all central tendencies should be considered definitions of average....

 of the absolute deviations and is a summary statistic

Summary statistics

In descriptive statistics, summary statistics are used to summarize a set of observations, in order to communicate the largest amount as simply as possible...

 of statistical dispersion

Statistical dispersion

In statistics, statistical dispersion is variability or spread in a variable or a probability distribution...

 or variability.