
ADHM construction
Encyclopedia
The ADHM construction or monad construction is the construction of all instanton
s using method of linear algebra by Michael Atiyah
, Vladimir G. Drinfel'd, Nigel. J. Hitchin, Yuri I. Manin
in their paper Construction of Instantons.
Then ADHM construction claims that, given certain regularity conditions,
gauge theory, the ADHM construction is identical but the moment map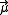 is set equal to the self-dual projection of the noncommutativity matrix of the spacetime times the identity matrix
is set equal to the self-dual projection of the noncommutativity matrix of the spacetime times the identity matrix
. In this case instantons exist even when the gauge group is U(1). The noncommutative instantons were discovered by Nikita Nekrasov
and Albert Schwarz
in 1998.
in a supersymmetric
gauge theory with an equal number of colors and flavors, as was demonstrated in Vortices, instantons and branes. The generalization to greater numbers of flavors appeared in Solitons in the Higgs phase: The Moduli matrix approach. In both cases the Fayet-Iliopoulos term, which determines a squark condensate
, plays the role of the noncommutativity parameter in the real moment map.
spacetime
coordinates written in quaternion
ic notation
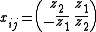 .
.
Consider the 2k × (N+2k) matrix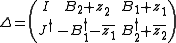 .
.
Then the conditions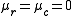 are equivalent to the factorization condition
are equivalent to the factorization condition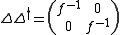 where f(x) is a k × k hermitian
where f(x) is a k × k hermitian
matrix.
Then a hermitian projection
operator P can be constructed as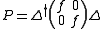 .
.
The nullspace of Δ(x) is of N dimension for generic x. The basis vector for this null-space can be assembled into an (N+2k) × N matrix U(x) with orthonormalization condition U†U=1.
A regularity condition on the rank of Δ guaranteed the completeness condition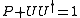
The anti-selfdual connection
is then constructed from U by the formula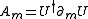 .
.
Instanton
An instanton is a notion appearing in theoretical and mathematical physics. Mathematically, a Yang–Mills instanton is a self-dual or anti-self-dual connection in a principal bundle over a four-dimensional Riemannian manifold that plays the role of physical space-time in non-abelian gauge theory...
s using method of linear algebra by Michael Atiyah
Michael Atiyah
Sir Michael Francis Atiyah, OM, FRS, FRSE is a British mathematician working in geometry.Atiyah grew up in Sudan and Egypt but spent most of his academic life in the United Kingdom at Oxford and Cambridge, and in the United States at the Institute for Advanced Study...
, Vladimir G. Drinfel'd, Nigel. J. Hitchin, Yuri I. Manin
Yuri I. Manin
Yuri Ivanovitch Manin is a Soviet/Russian/German mathematician, known for work in algebraic geometry and diophantine geometry, and many expository works ranging from mathematical logic to theoretical physics.-Biography:...
in their paper Construction of Instantons.
ADHM data
The ADHM construction uses the following data:- complex vector spaces V and W of dimension k and N,
- k × k complex matrices B1, B2, a k × N complex matrix I and a N × k complex matrix J,
- a realReal numberIn mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
moment mapMoment mapIn mathematics, specifically in symplectic geometry, the momentum map is a tool associated with a Hamiltonian action of a Lie group on a symplectic manifold, used to construct conserved quantities for the action. The moment map generalizes the classical notions of linear and angular momentum...
 ,
, - a complexComplex numberA complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
moment map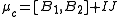 .
.
Then ADHM construction claims that, given certain regularity conditions,
- Given B1, B2, I, J such that
 , an Anti-Self-Dual instantonInstantonAn instanton is a notion appearing in theoretical and mathematical physics. Mathematically, a Yang–Mills instanton is a self-dual or anti-self-dual connection in a principal bundle over a four-dimensional Riemannian manifold that plays the role of physical space-time in non-abelian gauge theory...
, an Anti-Self-Dual instantonInstantonAn instanton is a notion appearing in theoretical and mathematical physics. Mathematically, a Yang–Mills instanton is a self-dual or anti-self-dual connection in a principal bundle over a four-dimensional Riemannian manifold that plays the role of physical space-time in non-abelian gauge theory...
in a SU(N)Special unitary groupThe special unitary group of degree n, denoted SU, is the group of n×n unitary matrices with determinant 1. The group operation is that of matrix multiplication...
gauge theoryGauge theoryIn physics, gauge invariance is the property of a field theory in which different configurations of the underlying fundamental but unobservable fields result in identical observable quantities. A theory with such a property is called a gauge theory...
with instantonInstantonAn instanton is a notion appearing in theoretical and mathematical physics. Mathematically, a Yang–Mills instanton is a self-dual or anti-self-dual connection in a principal bundle over a four-dimensional Riemannian manifold that plays the role of physical space-time in non-abelian gauge theory...
number k can be constructed, - All Anti-Self-Dual instantons can be obtained in this way and are in one-to-one correspondence with solutions up to a U(k) rotation which acts on each B in the adjoint representationAdjoint representationIn mathematics, the adjoint representation of a Lie group G is the natural representation of G on its own Lie algebra...
and on I and J via the fundamentalFundamental representationIn representation theory of Lie groups and Lie algebras, a fundamental representation is an irreducible finite-dimensional representation of a semisimple Lie group...
and antifundamental representations - The metricMetric (mathematics)In mathematics, a metric or distance function is a function which defines a distance between elements of a set. A set with a metric is called a metric space. A metric induces a topology on a set but not all topologies can be generated by a metric...
on the moduli spaceModuli spaceIn algebraic geometry, a moduli space is a geometric space whose points represent algebro-geometric objects of some fixed kind, or isomorphism classes of such objects...
of instantons is that inherited from the flat metric on B, I and J.
Noncommutative instantons
In a noncommutativeNoncommutative geometry
Noncommutative geometry is a branch of mathematics concerned with geometric approach to noncommutative algebras, and with construction of spaces which are locally presented by noncommutative algebras of functions...
gauge theory, the ADHM construction is identical but the moment map
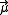 is set equal to the self-dual projection of the noncommutativity matrix of the spacetime times the identity matrix
is set equal to the self-dual projection of the noncommutativity matrix of the spacetime times the identity matrixIdentity matrix
In linear algebra, the identity matrix or unit matrix of size n is the n×n square matrix with ones on the main diagonal and zeros elsewhere. It is denoted by In, or simply by I if the size is immaterial or can be trivially determined by the context...
. In this case instantons exist even when the gauge group is U(1). The noncommutative instantons were discovered by Nikita Nekrasov
Nikita Nekrasov
-Background:Nerkrasov was born in Moscow, Russia and attended the Moscow State 57th School, graduating in 1995. He went on to graduate with honors from Moscow Physical Technical Institute in 1995. Nekrasov did his graduate work at Princeton University, receiving his PhD in 1996...
and Albert Schwarz
Albert Schwarz
Albert S. Schwarz is a mathematician and a theoretical physicist educated in Soviet Union and now a Professor at the University of California-Davis. He is one of the pioneers of Morse theory and brought up the first example of a topological quantum field theory. Schwarz worked on some examples in...
in 1998.
Vortices
Setting B2 and J to zero, one obtains the classical moduli space of nonabelian vorticesAbrikosov vortex
In superconductivity, an Abrikosov vortex is a vortex of supercurrent in a type-II superconductor. The supercurrent circulates around the normal core of the vortex. The core has a size \sim\xi — the superconducting coherence length...
in a supersymmetric
Supersymmetry
In particle physics, supersymmetry is a symmetry that relates elementary particles of one spin to other particles that differ by half a unit of spin and are known as superpartners...
gauge theory with an equal number of colors and flavors, as was demonstrated in Vortices, instantons and branes. The generalization to greater numbers of flavors appeared in Solitons in the Higgs phase: The Moduli matrix approach. In both cases the Fayet-Iliopoulos term, which determines a squark condensate
Condensate
Condensate may refer to:* The liquid phase produced by the condensation of steam or any other gas* The product of a chemical condensation reaction, other than water* Natural gas condensate, in the natural gas industry- Quantum physics :...
, plays the role of the noncommutativity parameter in the real moment map.
The construction formula
Let x be the 4-dimensional EuclideanEuclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
spacetime
Spacetime
In physics, spacetime is any mathematical model that combines space and time into a single continuum. Spacetime is usually interpreted with space as being three-dimensional and time playing the role of a fourth dimension that is of a different sort from the spatial dimensions...
coordinates written in quaternion
Quaternion
In mathematics, the quaternions are a number system that extends the complex numbers. They were first described by Irish mathematician Sir William Rowan Hamilton in 1843 and applied to mechanics in three-dimensional space...
ic notation
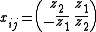 .
.Consider the 2k × (N+2k) matrix
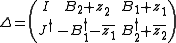 .
.Then the conditions
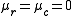 are equivalent to the factorization condition
are equivalent to the factorization condition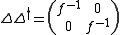 where f(x) is a k × k hermitian
where f(x) is a k × k hermitianHermitian
A number of mathematical entities are named Hermitian, after the mathematician Charles Hermite:*Hermitian adjoint*Hermitian connection, the unique connection on a Hermitian manifold that satisfies specific conditions...
matrix.
Then a hermitian projection
Projection (linear algebra)
In linear algebra and functional analysis, a projection is a linear transformation P from a vector space to itself such that P2 = P. It leaves its image unchanged....
operator P can be constructed as
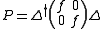 .
.The nullspace of Δ(x) is of N dimension for generic x. The basis vector for this null-space can be assembled into an (N+2k) × N matrix U(x) with orthonormalization condition U†U=1.
A regularity condition on the rank of Δ guaranteed the completeness condition
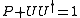
The anti-selfdual connection
Connection (mathematics)
In geometry, the notion of a connection makes precise the idea of transporting data along a curve or family of curves in a parallel and consistent manner. There are a variety of kinds of connections in modern geometry, depending on what sort of data one wants to transport...
is then constructed from U by the formula
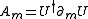 .
.

